Isolerade singulära punkter. Isolerade singulära punkter, deras klassificering

Definition. Funktionens singularpunkt kallas isolerat, om i någon omgivning av denna punkt finns en analytisk funktion (det vill säga analytisk i ringen).

Klassificeringen av isolerade singulära punkter för en funktion är relaterad till beteendet hos denna funktion i ett grannskap av en singulär punkt.

Definition. Punkten kallas disponibel en singularis för en funktion om det finns en ändlig gräns för denna funktion vid .

Exempel 5 Visa att funktionen har en borttagbar singularitet vid en punkt.

Lösning. Påminner om den första anmärkningsvärda gränsen, vi beräknar

Detta betyder att den givna funktionen har en borttagbar singularitet vid punkten.

Uppgift 4. Visa att spetsen är borttagbar för .

Definition. Punkten kallas Pol funktion , om denna funktion ökar oändligt för , det vill säga .

Låt oss uppmärksamma sambandet mellan begreppen noll och pol för en analytisk funktion. Låt oss representera funktionen som .

Om en punkt är en enkel nolla för en funktion, så har funktionen en enkel pol

Om punkten är ordningen noll för funktionen, så är det för funktionen polen ordning.

Exempel 6 Visa att funktionen har en tredje ordningens pol vid en punkt.

Lösning. Förutsatt att vi får. Eftersom vi tenderar till noll, enligt vilken lag som helst, har vi . Sedan, och med det, ökar själva funktionen i det oändliga. Därför, det vill säga singularpunkten är en pol. För en funktion är denna punkt uppenbarligen en trippel nolla. Därför är punkten för denna funktion en pol av tredje ordningen.

Uppgift 5. Visa att spetsen har en enkel pol.

Definition. Punkten kallas i grunden speciell punkt för funktionen om det vid denna tidpunkt varken finns en ändlig eller oändlig gräns för funktionen (funktionen för funktionen är inte definierad).

Låt vara en väsentlig singular punkt i funktionen. Sedan för alla förtilldelade komplexa tal finns det en sådan sekvens av punkter som konvergerar till , längs vilken värdena tenderar att: ( Sochockis sats).

Exempel 7 Visa att en funktion vid en punkt har en väsentlig singularitet.

Lösning. Betrakta beteendet hos en given funktion i närheten av punkten. För längs den positiva delen av den reella axeln (dvs ) har vi och ; om längs den negativa delen av den reella axeln (dvs.), då och . Så det finns ingen gräns för . Per definition har en funktion en väsentlig singularitet vid en punkt.

Låt oss betrakta funktionens beteende vid noll ur Sochocki-satsens synvinkel. Låta vara vilket komplext tal som helst förutom noll och oändlighet.

Från jämlikhet finner vi . Om vi ​​antar att vi får en sekvens av punkter, . Självklart, . Vid varje punkt i denna sekvens är funktionen lika med , och därför

Uppgift 6. Visa att funktionen har en väsentlig singularitet vid en punkt.

En punkt i oändligheten anses alltid vara speciell för funktionen. En punkt kallas en isolerad singularpunkt för en funktion om denna funktion inte har några andra singularpunkter utanför någon cirkel som är centrerad vid origo.

Klassificeringen av isolerade singulära punkter kan också utvidgas till fallet.

Exempel 8 Visa att funktionen har en dubbelpol i oändligheten.

Lösning. Betrakta funktionen , där är en analytisk funktion i närheten av punkten , och . Det betyder att funktionen har en dubbel nolla i oändligheten, men då för funktionen är punkten en dubbelpol.

Exempel 9 Visa att funktionen har en väsentlig singularitet i oändligheten.

Lösning. Ett liknande problem tas upp i pr.7. Betrakta beteendet hos en funktion i närheten av en oändligt avlägsen punkt. För längs den positiva delen av den reella axeln, och för längs den negativa delen av den reella axeln. Detta betyder att det inte finns någon gräns för funktionen vid en punkt och, i kraft av definitionen, är denna punkt i huvudsak singular.

Arten av singulariteten för en funktion vid en punkt kan bedömas utifrån huvudsak Laurent expansion i ett område av denna punkt.

Sats 1. För poängen disponibel singular punkt av funktionen , är det nödvändigt och tillräckligt att motsvarande Laurent expansion innehöll inte huvuddelen.

Uppgift 6. Med hjälp av Taylor-expansionen av funktionen i närheten av punkten, visa att den har en borttagbar singularitet vid noll.

Sats 2. För poängen Pol funktioner , är nödvändigt och tillräckligt så att huvudsak motsvarande Laurent expansion innehöll ett begränsat antal medlemmar :

Numret på den högsta negativa termen bestämmer ordningen på polen.

I detta fall kan funktionen representeras som

där är funktionen analytisk vid punkten, , är ordningen på polen.

Exempel 10 Visa att funktionen har enkla poler vid punkter.

Lösning. Låt oss överväga en punkt. Vi använder Laurent-expansionen av denna funktion i närheten av denna punkt, erhållen i exempel 2:

Eftersom den högsta (och enda) negativa effekten i huvuddelen av denna expansion är lika med en, är punkten en enkel pol för denna funktion.

Detta resultat kunde ha erhållits på annat sätt. Låt oss representera i form och sätta - detta är en funktion som är analytisk vid punkten och . På grund av (8) har denna funktion en enkel pol vid punkten.

Ett annat sätt: betrakta en funktion som har en enkel nolla vid punkten. Därför har den vid denna tidpunkt en enkel stolpe.

På liknande sätt, om vi skriver funktionen i formen , där är en funktion analytisk vid punkten och , då är det omedelbart tydligt att punkten är en enkel pol av funktionen .

Uppgift 7. Visa att funktionen har en pol av 2:a ordningen vid punkten och en pol av 4:e ordningen vid punkten.

Sats 3. För poängen i grunden speciell punkt av funktionen , är det nödvändigt och tillräckligt att huvudsak Laurent expansion i ett grannskap av punkten innehöll ett oändligt antal medlemmar .

Exempel 11. Bestäm arten av singulariteten vid punkten för funktionen

Lösning. I den välkända expansionen av cosinus lägger vi istället för:

Därför har Laurent-expansionen i ett område av en punkt formen

Här är den korrekta delen en term. Och huvuddelen innehåller ett oändligt antal termer, så poängen är i huvudsak singular.

Uppgift 8. Visa att funktionen vid ett tillfälle har en väsentlig singularitet.

Överväg någon funktion och skriv ner dess Laurent-expansion vid punkten:

Låt oss byta ut medan poängen går till punkten . Nu, i ett område av en punkt i oändligheten, har vi

Det återstår att införa en ny beteckning . Vi får

var är huvuddelen, och är den regelbundna delen av Laurents expansion av funktionen i närheten av en oändligt avlägsen punkt. Sålunda, i Laurent-expansionen av en funktion i närheten av en punkt, är huvuddelen en serie i positiva potenser, medan den korrekta delen är en serie i negativa potenser. Med hänsyn till detta

Ovanstående kriterier för att bestämma singularitetens natur förblir emellertid giltiga för en oändligt avlägsen punkt.

Exempel 12. Ta reda på arten av singulariteten för funktionen vid punkten. , då kan det vid ett tillfälle visa sig vara oisolerat.

Exempel 15 Funktionen på en oändligt avlägsen punkt har en väsentlig singularitet. Visa att punkten för funktionen inte är en isolerad singularis.

Lösning. Funktionen har ett oändligt antal poler vid nollorna i nämnaren, det vill säga vid punkterna , . Eftersom , då punkten , i vilket område som helst där det finns poler , är gränspunkten för polerna.

Modeller beskrivna av system med två autonoma differentialekvationer.

fasplan. Fas porträtt. isoklin metod. huvudsakliga isokliner. Steady State Stabilitet. Linjära system. Viktiga punkttyper: nod, sadel, fokus, center. Exempel: första ordningens kemiska reaktioner.

De mest intressanta resultaten om kvalitativ modellering av egenskaperna hos biologiska system erhölls på modeller av två differentialekvationer, som möjliggör en kvalitativ studie med metoden fasplan. Betrakta ett system av två autonoma ordinarie differentialekvationer av den allmänna formen

(4.1)

P(x,y), Q(x,y)- kontinuerliga funktioner definierade i någon domän G Euklidiskt plan ( x,y- Kartesiska koordinater) och har i detta område kontinuerliga derivator av ordning som inte är lägre än den första.

Område G kan vara obegränsad eller begränsad. Om variabler x, y har en specifik biologisk betydelse (koncentrationer av ämnen, överflöd av arter), oftast området Gär den positiva kvadranten av det högra halvplanet:

0 £ x< ¥ ,0 £ y< ¥ .

Koncentrationerna av ämnen eller förekomsten av arter kan också begränsas ovanifrån av kärlets volym eller av livsmiljöns yta. Variabelområdet har då formen:

0 £ x< x 0 , 0 £ y< y 0 .

Variabler x, y förändring i tid i enlighet med ekvationssystemet (4.1), så att varje tillstånd i systemet motsvarar ett par värden av variabler ( x, y).

Omvänt, för varje par av variabler ( x, y) motsvarar ett visst tillstånd i systemet.

Betrakta ett plan med koordinataxlar på vilket värdena för variabler plottas x,y. Varje punkt M detta plan motsvarar ett visst tillstånd i systemet. Ett sådant plan kallas fasplanet och visar helheten av alla tillstånd i systemet. Punkten M(x, y) kallas den avbildande eller representerande punkten.

Låt vid den första tiden t=t 0 representerar punktkoordinater M 0 (x(t 0),y(t 0)). Vid varje nästa ögonblick i tiden t den avbildande punkten kommer att flyttas i enlighet med förändringar i variablernas värden x(t),y(t). Uppsättning poäng M(x(t), y(t)) på fasplanet, vars position motsvarar systemets tillstånd i färd med att ändra variabler över tiden x(t), y(t) enligt ekvation (4.1), kallas fasbana.

Uppsättningen av fasbanor för olika initiala värden för variablerna ger ett lätt synligt "porträtt" av systemet. Byggnad fasporträtt låter dig dra slutsatser om arten av förändringar i variabler x, y utan att känna till de analytiska lösningarna för det ursprungliga ekvationssystemet(4.1).

För att avbilda ett fasporträtt är det nödvändigt att konstruera ett vektorfält av riktningar för systembanorna vid varje punkt i fasplanet. Genom att ange ett inkrementD t>0,vi får motsvarande ökningar D x och D y från uttryck:

D x=P(x,y)D t,

D y=Q(x,y)D t.

vektor riktning dy/dx vid punkt ( x, y) beror på funktionernas tecken P(x, y), Q(x, y) och kan ges av en tabell:

P(x,y)>0,Q(x,y)>0
P(x,y)<0,Q(x,y)<0
P(x,y)>0,Q(x,y)<0
P(x,y)<0,Q(x,y)>0

.(4.2)

Lösning på denna ekvation y=y(x, c), eller implicit F(x,y)=c, var Medär integrationskonstanten, ger familjen av integralkurvor i ekvationen (4.2) - fasbanor system (4.1) på planet x, y.

Isoklin metod

För att konstruera ett fasporträtt använder man isoklin metod - linjer ritas på fasplanet som skär integralkurvorna i en specifik vinkel. Den isoklina ekvationen är lätt att få från (4.2). Låt oss sätta

var MEN– en viss konstant. Menande MEN representerar tangenten för lutningen av tangenten till fasbanan och kan ta värden från -¥ till + ¥ . Ersätter istället för dy/dx i (4.2) kvantiteten MEN vi får den isoklina ekvationen:

.(4.3)

Ekvation (4.3) bestämmer vid varje punkt i planet den enda tangenten till motsvarande integralkurva, förutom den punkt där P(x,y)= 0, Q (x,y) = 0 , i vilken tangentens riktning blir obestämd, eftersom värdet på derivatan blir obestämd:

.

Denna punkt är skärningspunkten för alla isokliner - speciell punkt. Det försvinner samtidigt tidsderivatorna av variablerna x och y.

Således, vid singularpunkten, är förändringshastigheterna för variabler lika med noll. Därför motsvarar singularpunkten för differentialekvationerna för fasbanor (4.2) systemets stationära tillstånd(4.1), och dess koordinater är de stationära värdena för variablerna x, y.

Av särskilt intresse är huvudsakliga isokliner:

dy/dx=0, P(x,y)=0 – isoklin av horisontella tangenter och

dy/dx=¥ , Q(x,y)=0 – isoklin av vertikala tangenter.

Genom att konstruera de huvudsakliga isoklinerna och hitta punkten för deras skärningspunkt (x,y), vars koordinater uppfyller villkoren:

vi kommer alltså att finna skärningspunkten för alla isokliner i fasplanet, vid vilken riktningen för tangenterna till fasbanorna är obestämd. Det - singulära punkt, vilket motsvarar systemets stationära tillstånd(Fig. 4.2).

System (4.1) har lika många stationära tillstånd som det finns skärningspunkter för huvudisoklinerna på fasplanet.

Varje fasbana motsvarar en uppsättning rörelser i ett dynamiskt system som passerar genom samma tillstånd och skiljer sig från varandra endast vid början av tidsreferensen.

Om villkoren för Cauchy-satsen är uppfyllda, då genom varje punkt i rummet x, y, t passerar genom en enda integralkurva. Detsamma gäller, tack vare autonomi, för fasbanor: en unik fasbana passerar genom varje punkt i fasplanet.

Steady State Stabilitet

Låt systemet vara i jämvikt.

Då är den representativa punkten belägen vid en av de singulära punkterna i systemet, där, per definition:

.

Huruvida en singulär punkt är stabil eller inte bestäms av om den representativa punkten lämnar eller inte med en liten avvikelse från det stationära tillståndet. Som tillämpat på ett system med två ekvationer, definitionen av stabilitet i språkete, dsom följer.

Jämviktstillståndet är stabilt om för ett givet område av avvikelser från jämviktstillståndet (e )område kan anges d (e ), som omger jämviktstillståndet och har egenskapen att ingen bana som börjar inuti regionen d , kommer aldrig att nå gränsen e . (Fig. 4.4)

För en stor klass av system - grova system – vars beteende inte förändras med en liten förändring i typen av ekvationer, information om typen av beteende i närheten av det stationära tillståndet kan erhållas genom att inte studera originalet, utan det förenklade linjäriserad systemet.

Linjära system.

Betrakta ett system av två linjära ekvationer:

.(4.4)

Här a, b, c, d- konstanter, x, y- Kartesiska koordinater på fasplanet.

Den allmänna lösningen kommer att sökas i formen:

.(4.5)

Ersätt dessa uttryck i (4.4) och reducera med e l t:

(4.6)

Algebraiskt ekvationssystem (4.6) med okända A, B har en lösning som inte är noll endast om dess determinant, sammansatt av koefficienterna för de okända, är lika med noll:

.

Genom att expandera denna determinant får vi den karakteristiska ekvationen för systemet:

.(4.7)

Lösningen av denna ekvation ger värdena på indikatornl 1,2 , under vilka värden som inte är noll är möjliga för A och B lösningar av ekvation (4.6). Dessa värden är

.(4.8)

Om det radikala uttrycket är negativt, alltsål 1,2 komplexa konjugerade tal. Antag att båda rötterna i ekvationen (4.7) har reella delar som inte är noll och att det inte finns några multipla rötter. Då kan den allmänna lösningen av systemet (4.4) representeras som en linjär kombination av exponenter med exponenterl 1 , l 2 :

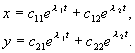(4.9)

För att analysera karaktären av de möjliga banorna för systemet på fasplanet använder vi linjär homogen koordinattransformation, som kommer att föra systemet till kanonisk form:

,(4.10)

vilket möjliggör en mer bekväm representation på fasplanet jämfört med det ursprungliga systemet (4.4). Låt oss introducera nya koordinaterξ , η enligt formlerna:

(4.1)

Det är känt från förloppet av linjär algebra att om de reella delarna inte är lika med nolll 1 , l 2 det ursprungliga systemet (4.4) med hjälp av transformationer (4.11) kan alltid transformeras till den kanoniska formen (4.10) och dess beteende på fasplanet kan studerasξ , η . Tänk på de olika fall som kan dyka upp här.

Rötter λ 1 , λ 2 – giltig och av samma tecken

I det här fallet är transformationskoefficienterna reella, vi rör oss från det verkliga planetx,ytill det verkliga planet ξ, η. Genom att dividera den andra av ekvationerna (4.10) med den första får vi:

.(4.12)

Genom att integrera denna ekvation finner vi:

Var .(4.13)

Låt oss komma överens om att förstå med λ 2 roten till den karakteristiska ekvationen med stor modul, vilket inte bryter mot det allmänna i vårt resonemang. Sedan, eftersom i det aktuella fallet rötterna λ 1 , λ2 – giltig och av samma tecken,a>1 , och vi har att göra med integralkurvor av paraboltyp.

Alla integralkurvor (förutom axeln η , vilket motsvarar ) rör vid axelns utgångspunkt ξ, som också är en integralkurva av ekvation (4.11). Ursprunget till koordinater är en singulär punkt.

Låt oss nu ta reda på rörelseriktningen för den representativa punkten längs fasbanorna. Om λ 1, λ2 är negativa, så som framgår av ekvationerna (4.10), |ξ|, |η| minska med tiden. Den representerande punkten närmar sig ursprunget, men når det aldrig. Annars skulle detta motsäga Cauchys teorem, som säger att endast en fasbana passerar genom varje punkt i fasplanet.

En sådan singulär punkt genom vilken integralkurvor passerar, precis som en familj av paraboler passerar genom origo, kallas en nod (fig. 4.5)

Jämviktstillstånd av knuttyp vid λ 1, λ2 < 0 är stabil enligt Lyapunov, eftersom den representerande punkten rör sig längs alla integralkurvor mot koordinaternas ursprung. Det stabil knut. Om λ 1, λ2 > 0 då |ξ|, |η| ökar med tiden och den representativa punkten flyttar sig bort från origo. I det här fallet den singulära punkten– instabil knut .

På fasplanet x, y den allmänna kvalitativa karaktären hos integralkurvornas beteende kommer att finnas kvar, men tangenterna till integralkurvorna kommer inte att sammanfalla med koordinataxlarna. Lutningsvinkeln för dessa tangenter kommer att bestämmas av förhållandet mellan koefficienterna α , β , γ , δ i ekvationer (4.11).

Rötter λ 1 , λ 2 är giltiga och har olika tecken.

Konvertera från koordinater x,y till koordinater ξ, η återigen verklig. Ekvationerna för de kanoniska variablerna har återigen formen (4.10), men nu är tecknen λ 1, λ2 annorlunda. Fasbanaekvationen har formen:

Var , (4.14)

Integrering (4.14), finner vi

(4.15)

Det ekvationen definierar en familj av kurvor av hyperbolisk typ, där båda koordinataxlarnaär asymptoterna (kl a=1 vi skulle ha en familj av likbenta hyperboler). Koordinataxlarna är också i detta fall integralkurvor– dessa kommer att vara de enda integralkurvorna som passerar genom origo. Varjevarav består av tre fasbanor: av två rörelser mot ett tillstånd av jämvikt (eller bort från ett jämviktstillstånd) och från ett tillstånd av jämvikt. Alla andra integralkurvor– är hyperboler som inte passerar genom ursprunget (fig. 4.6) Denna singulära punkt kallas "sadel ». Nivålinjerna nära fjällsadeln beter sig som fasbanor i närheten av sadeln.

Låt oss överväga arten av den representativa punktens rörelse längs fasbanor nära jämviktstillståndet. Låt t.ex.λ1 >0, λ2<0 . Sedan den representativa punkten placerad på axeln ξ , kommer att flytta sig bort från origo och placeras på axeln η – kommer på obestämd tid att närma sig koordinaternas ursprung, utan att nå den på ändlig tid. Varhelst den representerande punkten befinner sig i det initiala ögonblicket (med undantag för singularpunkten och punkter på asymptoten η =0), den kommer så småningom att röra sig bort från jämviktstillståndet, även om den i början rör sig längs en av integralkurvorna mot en singulär punkt.

Det är uppenbart singular spets av sadeltyp är alltid instabil . Endast under speciellt valda initiala förhållanden på asymptotenη =0 systemet kommer att närma sig ett tillstånd av jämvikt. Detta motsäger dock inte påståendet att systemet är instabilt. Om man räknar, att alla initialtillstånd i systemet på fasplanet är lika sannolika, då är sannolikheten för ett sådant initialtillstånd som motsvarar rörelse i riktningen till singular punkt är lika med noll. Därför kommer varje verklig rörelse att ta bort systemet från jämviktstillståndet.Går tillbaka till koordinaterx,y,vi får samma kvalitativa bild av karaktären av förflyttningen av banor runt ursprunget.

Gränsen mellan de betraktade fallen av en nod och en sadel är fallet när en av de karakteristiska indikatorerna, till exempel λ 1 , försvinner, vilket inträffar när systemets determinant- uttryck adbc=0(se formel 4.8 ). I detta fall är koefficienterna för ekvationernas högra sida (4.4) proportionella mot varandra:

och systemet har för sina jämviktstillstånd alla punkter på linjen:

De återstående integralkurvorna är en familj av parallella linjer med en lutning , längs vilka de representativa punkterna antingen närmar sig jämviktstillståndet eller flyttar sig bort från det, beroende på tecknet för den andra roten av den karakteristiska ekvationen λ 2 = a+d.(Fig. 4. 7 ) I detta fall beror koordinaterna för jämviktstillståndet på variablernas initiala värde.

Rötter λ 1 , λ 2 – komplexkonjugera

I det här fallet på riktigtx och y vi ska har komplexa konjugat ξ , η (4.10) . Men genom att införa ytterligare en mellanliggande transformation är det även i detta fall möjligt att reducera hänsynen till en verklig linjär homogen transformation. Låt oss sätta:

(4.16)

var a, b, och u, v – verkliga värden. Det kan visas att omvandlingen fr.o.mx,y till u, v är, enligt våra antaganden, reell, linjär, homogen med en determinant som inte är noll. På grund av ekvationerna(4.10, 4.16) har vi:

var

(4.17)

Att dividera den andra av ekvationerna med den första, vi får:

som är lättare att integrera, om vi byter till det polära koordinatsystemet (r, φ ) . Efter byte vi får varifrån:

.(4.18)

Alltså på fasplanetu, vvi har att göra med en familj av logaritmiska spiraler, som var och en harasymptotisk punkt vid ursprunget.Singular punkt som är den asymptotiska punkten för alla integralkurvor som har formen av spiraler, kapslade vän ivän, ringde fokus ( fig.4.8 ) .

Låt oss överväga arten av rörelsen av den representerande punkten längs fasbanorna. Multiplicera den första av ekvationerna (4.17) medu, och den andra till v och lägger till får vi:

Var

Låta a 1 < 0 (a 1 = Reλ ) . Den representerande punkten närmar sig sedan kontinuerligt ursprunget utan att nå det på en begränsad tid. Detta betyder att fasbanorna är vridande spiraler och motsvarar dämpade svängningar variabler. Det - stadigt fokus .

I fallet med ett stabilt fokus, som i fallet med en stabil nod, är inte bara Lyapunov-villkoret uppfyllt, utan också ett strängare krav. Nämligen, för eventuella initiala avvikelser kommer systemet så småningom att återgå så nära som önskat till jämviktsläget. Sådan stabilitet, där de initiala avvikelserna inte bara ökar, utan sönderfaller, som tenderar till noll, kallas absolut stabilitet .

Om i formeln (4.18) a 1 >0 , då rör sig den representerande punkten bort från ursprunget, och vi har att göra med instabilt fokus . När du flyttar från ett planu, vtill fasplanetx, yspiraler kommer också att förbli spiraler, men kommer att deformeras.

Tänk nu på fallet nära 1 =0 . Fasbanor på planetu, vdet kommer att finnas cirklar som på planetx,ypassa ellipser:

Alltså klen 1=0 genom en speciell punktx= 0,y= 0 ingen integralkurva passerar. En sådan isolerad singularpunkt, nära vilken integralkurvorna är slutna kurvor, i synnerhet ellipser inbäddade i varandra och omsluter singularpunkten, kallas ett centrum.

Således är sex typer av jämvikt möjliga, beroende på arten av rötterna till den karakteristiska ekvationen (4.7). Vy över fasbanor på planet x, y för dessa sex fall visas i fig. 4.9.

Ris. 4.9.Typer av fasporträtt i närheten av ett stationärt tillstånd för systemet med linjära ekvationer (4.4).

De fem typerna av jämviktstillstånd är grova, deras natur förändras inte med tillräckligt små förändringar i ekvationernas högra sida (4.4). I det här fallet bör förändringarna vara små inte bara på högersidan utan även i deras första ordningens derivator. Det sjätte jämviktstillståndet - centrum - är inte grovt. Med små förändringar i parametrarna på höger sida av ekvationerna går det in i ett stabilt eller instabilt fokus.

Bifurkationsdiagram

Låt oss presentera notationen:

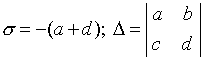. (4.11)

Sedan kan den karakteristiska ekvationen skrivas i formen:

. (4.12)

Betrakta ett plan med rektangulära kartesiska koordinater s , D och markera på den de områden som motsvarar en eller annan typ av jämviktstillstånd, vilket bestäms av arten av rötterna till den karakteristiska ekvationen

.(4.13)

Villkoret för stabiliteten i jämviktstillståndet kommer att vara närvaron av en negativ reell del av yl 1 och l 2 . En nödvändig och tillräcklig förutsättning för detta är uppfyllandet av ojämlikheternas > 0, D > 0 . På diagrammet (4.15) motsvarar detta tillstånd punkterna som ligger i den första fjärdedelen av parameterplanet. Singularpunkten kommer att vara fokus oml 1 och l 2 komplex. Detta tillstånd motsvarar de punkter på planet för vilka , de där. punkter mellan två grenar av en parabels 2 = 4 D. Halvaxelpunkter s = 0, D>0, motsvarar jämviktstillstånd av centrumtypen. Likaså,l 1 och l 2 - giltiga, men olika tecken, dvs. en singular punkt kommer att vara en sadel om D<0, etc. Som ett resultat får vi ett partitionsdiagram av parameterplanet s, D, i regioner som motsvarar olika typer av jämviktstillstånd.

Ris. 4.10. Bifurkationsdiagram

för systemet med linjära ekvationer 4.4

Om koefficienterna för det linjära systemet a, b, c, d beror på någon parameter, sedan när denna parameter ändras kommer värdena också att ändrass , D . När man passerar genom gränserna förändras fasporträttets karaktär kvalitativt. Därför kallas sådana gränser för bifurkationsgränser - på motsatta sidor om gränsen har systemet två topologiskt olika fasporträtt och följaktligen två olika typer av beteende.

Diagrammet visar hur sådana förändringar kan ske. Om vi ​​utesluter specialfall - ursprunget för koordinater - så är det lätt att se att sadeln kan gå in i en nod, stabil eller instabil när den korsar y-axeln. En stabil nod kan antingen flytta till en sadel eller ett stabilt fokus, och så vidare. Observera att övergångarna mellan stabil nod-stabilt fokus och instabil nod-instabil fokusövergångar inte är bifurkationella, eftersom topologin för fasutrymmet inte ändras i detta fall. Vi kommer att prata mer i detalj om topologin för fasrummet och bifurkationsövergångar i föreläsning 6.

Under bifurkationsövergångar ändras karaktären av stabiliteten hos singularpunkten. Till exempel kan ett stabilt fokus genom mitten förvandlas till ett instabilt fokus. Denna bifurkation kallas Andronov-Hopf bifurkation med namnen på forskarna som studerade det. Med denna bifurkation i olinjära system föds en gränscykel, och systemet blir självsvängande (se föreläsning 8).

Exempel. System av linjära kemiska reaktioner

Ämne X strömmar in utifrån med konstant hastighet, övergår till ämne Y och med en hastighet som är proportionell mot koncentrationen av ämnet Y, tas ut ur reaktionssfären. Alla reaktioner är av första ordningen, med undantag för inflödet av materia utifrån, som har ordningen noll. Reaktionsschemat ser ut så här:

(4.14)

och beskrivs av ekvationssystemet:

(4.15)

Vi får stationära koncentrationer genom att likställa de högra sidorna med noll:

.(4.16)

Tänk på fasporträttet av systemet. Låt oss dividera den andra ekvationen av systemet (4.16) med den första. Vi får:

.(4.17)

Ekvation (4.17) bestämmer beteendet hos variabler på fasplanet. Låt oss konstruera ett fasporträtt av detta system. Först ritar vi huvudisoklinerna på fasplanet. Ekvationen för isoklinen för vertikala tangenter:

Ekvation för isoklinen för horisontella tangenter:

Singularpunkten (stationärt tillstånd) ligger i skärningspunkten mellan de huvudsakliga isoklinerna.

Låt oss nu bestämma i vilken vinkel koordinataxlarna skär integralkurvorna.

Om en x= 0, då.

Således tangenten för lutningen av tangenten till integralkurvorna y=y(x), korsar y-axeln x=0, är negativ i det övre halvplanet (kom ihåg att variablerna x, y har koncentrationsvärden, och därför är vi bara intresserade av den övre högra kvadranten av fasplanet). I detta fall ökar värdet på tangenten för tangentens lutningsvinkel med avståndet från origo.

Tänk på axeln y= 0. Vid skärningspunkten för denna axel beskrivs integralkurvorna av ekvationen

På tangenten för lutningen för integralkurvorna som korsar abskissaxeln är positiv och ökar från noll till oändligt med ökande x.

Kl.

Sedan, med en ytterligare ökning, minskar lutningens tangent i absolut värde, förblir negativ och tenderar till -1 vid x ® ¥ . Genom att känna till riktningen för tangenterna till integralkurvorna på huvudisoklinerna och på koordinataxlarna är det lätt att konstruera hela bilden av fasbanor.

Beskaffenheten av stabiliteten hos den singulara punkten kommer att fastställas med Lyapunov-metoden. Den karakteristiska determinanten för systemet har formen:

.

När vi expanderar determinanten får vi den karakteristiska ekvationen för systemet: , dvs. rötterna till den karakteristiska ekvationen är båda negativa. Därför är systemets stationära tillstånd en stabil nod. Samtidigt koncentrationen av ämnet X tenderar till ett stationärt tillstånd alltid monotont, koncentrationen av ämnet Y kan passera genom min eller max. Oscillerande regimer i ett sådant system är omöjliga.

Taylor-serier fungerar som ett effektivt verktyg för att studera funktioner som är analytiska i cirkeln zol För att studera funktioner som är analytiska i ett ringformigt område, visar det sig att det är möjligt att konstruera expansioner i positiva och negativa potenser (z - zq) av form som generaliserar Taylor-expansioner. Serien (1), förstås som summan av två serier, kallas Laurent-serien. Det är tydligt att konvergensområdet för serie (1) är den gemensamma delen av konvergensregionerna för var och en av serierna (2). Låt oss hitta henne. Konvergensområdet för den första serien är en cirkel vars radie bestäms av Cauchy-Hadamard-formeln Inuti konvergenscirkeln konvergerar serien (3) till en analytisk funktion, och i vilken cirkel som helst med mindre radie konvergerar den absolut och enhetligt. Den andra serien är en potensserie med avseende på variabeln. Serien (5) konvergerar inom sin konvergenscirkel till den analytiska funktionen av den komplexa variabeln m-*oo, och i varje cirkel med mindre radie konvergerar den absolut och enhetligt, vilket betyder att konvergensområdet för serien (4) är cirkelns utseende - Om det då finns ett gemensamt konvergensområde för serien (3) och (4) - en cirkulär ring i vilken serien (1) konvergerar till en analytisk funktion. Dessutom, i vilken ring som helst, konvergerar den absolut och enhetligt. Exempel 1. Bestäm konvergensområdet för rad Laurent-serien Isolerade singulära punkter och deras klassificering (z), som är enkelvärdig och opolitisk i en cirkulär ring, kan representeras i denna ring som summan av en konvergent serie vars koefficienter Cn bestäms unikt och beräknas av formlerna där 7p är en cirkel med radien m Låt oss fixera en godtycklig punkt z inuti ringen R Vi konstruerar cirklar med centrum i punkten r vars radier uppfyller ojämlikheterna och betraktar en ny ring. Enligt Cauchys integralsats för en multiplicerad domän har vi För alla punkter £ längs cirkeln 7d* är relationen de summan av en enhetligt konvergent serie 1 1 uppfylld. Därför kan bråket ^ representeras i vi- /" / På ett något annorlunda sätt, för alla punkter ξ på cirkeln ir> vi har relationen Därför kan bråket ^ representeras som summan av en enhetligt konvergent serie i formlerna (10) och (12) är analytiska funktioner i en cirkulär ring. Därför, enligt Cauchys sats, ändras inte värdena för motsvarande integraler om cirklarna 7/r och 7r/ ersätts av någon cirkel. Detta gör att vi kan kombinera formler (10) och (12). Genom att ersätta integralerna på höger sida av formel (8) med deras uttryck (9) respektive (11) får vi den önskade expansionen. Eftersom z är en godtycklig ringens punkt, följer det att serien ( 14) konvergerar till funktionen f(z) överallt i denna ring, och i vilken ring som helst konvergerar serien till denna funktion absolut och enhetligt. Låt oss nu bevisa att nedbrytningen av formen (6) är unik. Antag att ytterligare en sönderdelning äger rum.Då har vi överallt inuti ringen R På omkretsen konvergerar serien (15) likformigt. Multiplicera båda sidor av likheten (där m är ett fast heltal, och integrera båda serierna term för term. Som ett resultat får vi på vänster sida och till höger - Csh. Således, (4, \u003d St. Sedan m är ett godtyckligt tal, då den sista likhetsserien (6), vars koefficienter beräknas med formler (7), kallas Laurentserien för funktionen f(z) i ringen 7) för koefficienterna för Laurentserien är används sällan i praktiken, eftersom de som regel kräver besvärliga beräkningar. Vanligtvis, om möjligt, används färdiga Taylor-expansions av elementära funktioner. Baserat på expansionens unika, leder alla legitima metoder till samma resultat. Exempel 2 Betrakta Laurent-seriens expansioner av funktioner för olika domäner, anta att Fuiscius /(r) har två singulära punkter: Därför finns det tre ringdomäner och, centrerad vid punkten r = 0. i var och en av vilka funktionen f(r) är analytisk: a) cirkeln är cirkelns yttre (fig. 27). Låt oss hitta Laurent-expansionerna av funktionen /(z) i var och en av dessa regioner. Vi representerar /(z) som summan av elementära bråk. a) Cirkeltransformationsrelation (16) enligt följande. Genom att använda formeln för summan av termer av en geometrisk progression får vi b) Ringen för funktionen -z förblir konvergent i denna ring, eftersom Serie (19) för funktionen j^j för |z| > 1 avviker. Därför transformerar vi funktionen /(z) enligt följande: genom att använda formeln (19) igen, får vi det Denna serie konvergerar för. Genom att ersätta expansionerna (18) och (21) i relation (20) får vi c) Cirkelns yttre för funktionen -z med |z| > 2 divergerar och serier (21) för funktionen Låt oss representera funktionen /(z) i följande form: /<*> Med hjälp av formlerna (18) och (19) får vi OR 1. Detta exempel visar att för samma funktion f(z) har Laurentexpansionen generellt sett en annan form för olika ringar. Exempel 3. Hitta sönderdelningen av de 8 Laurent-serien av funktionen Laurent-serien Isolerade singulära punkter och deras klassificering i det ringformiga området A. Vi använder representationen av funktionen f (z) i följande form: och transformera den andra termen. formeln för summan av termerna för en geometrisk progression får vi. Genom att ersätta de hittade uttrycken i formeln (22) har vi exempel 4. Expandera funktionen i en Laurent-serie i närheten av tunn zq = 0. För vilken komplex som helst , vi har Låt Denna expansion är giltig för vilken punkt som helst z Ф 0. I det här fallet är det ringformade området hela det komplexa planet med en utslängd punkt z - 0. Denna region kan definieras av följande samband: Denna funktion är analytisk i regionen Från formler (13) för koefficienterna för Laurent-serien, med samma resonemang som i föregående stycke, kan man få Kouiw-ojämlikheterna. om funktionen f(z) är begränsad till en cirkel, där M är en konstant), så kallas isolerade singularpunkter En punkt zo kallas en isolerad singularpunkt för funktionen f(z) om det finns en ringformig grannskap av punkten ( denna mängd kallas ibland också en punkterad grannskap av punkten 2o), där funktionen f(z) är envärdig och analytisk. Vid själva punkten zo är funktionen antingen inte definierad eller är inte enkelvärdig och analytisk. Tre typer av singulära punkter särskiljs beroende på beteendet hos funktionen /(z) när man närmar sig punkten zo. En isolerad singularpunkt sägs vara: 1) borttagbar om det finns en finit 2) pmusach om 3) en väsentligen singularpunkt om funktionen f(z) inte har någon gräns för Sats 16. En isolerad singularpunkt z0 i en funktion f(z) är en borttagbar singularpunkt om och endast om Laurent-expansionen av funktionen f(z) i närheten av punkten zo inte innehåller en huvuddel, dvs. har formen Let zo - borttagbar singular punkt. Då finns det en finit funktion, därför är funktionen f(z) begränsad i en prokologisk grannskap av punkten r. Vi sätter i kraft av Cauchy-olikheterna Eftersom det är möjligt att välja p som godtyckligt liten, då alla koefficienter vid negativa potenser (z - 20) är lika med noll: Omvänt, låt Laurent expansionen av funktionen /(r) i närheten av punkten zq innehåller endast den korrekta delen, dvs den har formen (23) och, därför är Taylor. Det är lätt att se att för z -* z0 har funktionen /(r) ett gränsvärde: Sats 17. En isolerad singularpunkt zq för funktionen f(z) är borttagbar om och endast om funktionen J(z) är avgränsad i någon punkterad omgivning av punkten zq, Zgmechai inte. Låt r0 vara en borttagbar singularpunkt för f(r). Om vi ​​antar att funktionen f(r) är analytisk i någon cirkel centrerad i punkten th. Detta definierar namnet på punkten - engångs. Sats 18. En isolerad singularpunkt zq i en funktion f(z) är en pol om och endast om huvuddelen av Laurent-expansionen av funktionen f(z) i närheten av punkten innehåller ett ändligt (och positivt) tal av termer som inte är noll, d.v.s. har formen 4 Låt z0 vara en pol. Sedan dess finns det en punkterad omgivning av punkten z0 där funktionen f(z) är analytisk och inte noll. Sedan definieras en analytisk funktion i denna grannskap och följaktligen är punkten zq en borttagbar singularispunkt (noll) för funktionen eller där h(z) är en analytisk funktion, h(z0) ∩ 0. är analytisk i en grannskap av punkten zq, och varifrån vi får det. Låt oss nu anta att funktionen f(z) har en nedbrytning av formen (24) i en punkterad omgivning av punkten zo. Det betyder att i detta område är funktionen f(z) analytisk tillsammans med funktionen. För funktionen g(z) är expansionen giltig från vilken det är tydligt att zq är en borttagbar singularpunkt för funktionen g(z) och existerar. Sedan tenderar funktionen till 0 - funktionens pol. Det finns ytterligare en enkel faktum. Punkten Zq är en pol för funktionen f(z) om och endast om funktionen g(z) = y kan utökas till en analytisk funktion i närheten av punkten zq genom att sätta g(z0) = 0. Ordningen av polen för funktionen f(z) kallas nollordningen för funktionen jfa. Satserna 16 och 18 innebär följande påstående. Sats 19. En isolerad singular tunn är i huvudsak singular om och endast om huvuddelen av Laurentexpansionen i en punkterad omgivning av denna punkt innehåller oändligt många termer som inte är noll. Exempel 5. Funktionens singularpunkt är zo = 0. Vi har Laurent Series Isolerade singularpunkter och deras klassificering. Därför är zo = 0 en borttagbar singularpunkt. Expansionen av funktionen /(z) i en Laurent-serie i närheten av nollpunkten innehåller endast den korrekta delen: Exempel7. f(z) = Singularpunkten för funktionen f(z) är zq = 0. Betrakta beteendet hos denna funktion på den reella och imaginära axeln: på den reella axeln vid x 0, på den imaginära axeln Därför är varken finita eller oändlig gräns f(z) vid z -* 0 finns inte. Därför är punkten r0 = 0 en väsentligen singular punkt för funktionen f(z). Låt oss hitta Laurent-utvidgningen av funktionen f(z) i närheten av nollpunkten. För alla komplexa C har vi Vi ställer in. Sedan innehåller Laurent-expansionen ett oändligt antal termer med negativa potenser z.

Låta zq - singularis för funktionen f(z), t.s. F Z) men är analytisk vid denna tidpunkt (i synnerhet kanske inte definieras där). Om det finns en sådan punkterad grannskap av punkten zq (dvs. uppsättningen O z - zq f(z) är alltså aliatisk zo kallad isolerad singular punkt funktioner F Z). Denna definition finns också bevarad i målet zn = oo, om jod är ett punkterat område av en punkt zq = oo förstå uppsättningen z > jag - utseendet på någon cirkel centrerad vid ursprunget. Med andra ord singulära punkten zq sägs vara isolerad om det finns ett område i denna punkt där det finns andra singularpunkter som skiljer sig från zq. Överallt nedan betraktar vi endast singulära punkter med ett enskilt värde (funktionen F Z) antas vara unik).

Beroende på funktionens beteende F Z) på z -> zq Det finns tre typer av singulära punkter. Isolerad singular punkt zq funktioner F Z) kallad:

1) löstagbar singular spets om det finns en ändlig gräns

2) Pol om det finns en gräns

3) väsentlig punkt, om F Z) har varken en ändlig eller oändlig gräns för z-> zq.

EXEMPEL 26.1. Låt oss visa att alla tre typerna av singulära punkter realiseras. Överväga f(z)= punkt zq = 0 är isolerad

singular punkt för denna funktion. Med formeln (22.12) får vi expansionen

därav följer att det finns lim fi(z)= 1. Därför är zq = 0

är en löstagbar singular punkt för funktionen fi(z).

Fungera f'j(z) =--- har en stolpe vid en punkt zo= 1 eftersom

2 r"X

Tänk nu på funktionen )z(z)= e 1 ^ r och visa att zo = O är en väsentlig singular punkt för denna funktion. När man strävar z till noll längs den reella axeln, de vänstra och högra gränserna för funktionen f (z) olika: lim Med 1 / 1 = 0, lim med 1 /* = os. Detta innebär,

x->0-0 x->0+O

Vad f:i(z) har varken en ändlig eller oändlig gräns för 2 -> Åh, d.v.s. zq = 0 är en väsentligen singular punkt för denna funktion. (Observera det som punkten tenderar z-iy till noll på den imaginära axelfunktionen

har ingen gräns alls.)

Naturligtvis finns det också icke-isolerade singulära punkter. Till exempel. funktion har poler vid punkter z n = -, P= ±1, ±2,...

Följaktligen, Zq = 0 är en icke-isolerad singularpunkt för denna funktion: i vilken (godtyckligt liten) grannskap som helst av denna punkt finns det andra singularpunkter g sid.

Låta zo- slutliga isolerade singularpunkten för en funktion F Z). Sedan F Z)är liknande i något punkterat område 0 Zo av punkten zo denna grannskap kan betraktas som en ring med inre radie r = 0. Enligt sats 25.1, i grannskapet i fråga, funktionen F Z) kan utökas i en Laurent-serie (25.2). Vi kommer att visa att funktionens beteende för 2 -> zq (dvs typen av singular punkt zo) beror på formen av huvuddelen av nedbrytningen (25.2); denna omständighet förklarar ursprunget till termen "huvuddel".

SAT 2G.2. En isolerad singular punkt zo för en funktion f(z) kan tas bort om och endast om Lorap-expansionen i en punkterad omgivning av denna punkt har oiden

de där. består av endast den korrekta delen, och alla koefficienter för huvuddelen är lika med kulan.

Bevis. 1. Låt zoär en löstagbar singularis. Låt oss bevisa att Laurent expansion av funktionen F Z) har formen (26.1). Sedan singularpunkten zo löstagbar, då finns det en ändlig gräns lim f(z) = A. Följaktligen, F Z) avgränsad i något punkterat område 0 z - zq av punkten zo, de där. )(z) för alla z från detta kvarter. Ta någon R. U р /?|, och använd formlerna (25.3) för koefficienterna för Laurent-serien:

För koefficienterna för huvuddelen av expansionen n =- 1,-2,... För sådana värden P vi har p~n-e 0 kl R-> 0. Eftersom värdet R kan väljas godtyckligt liten, då Mr~" kan vara godtyckligt liten. Eftersom |c t,| ^ Mr~n och cn är inte beroende av p, då cn = 0 för och= - 1, -2,..., vilket skulle bevisas.

2. Låt oss nu anta att Laurent-expansionen har formen (26.1). Series (26.1) är en kraftserie och. konvergerar därför inte bara i den punkterade, utan också i hela grannskapet z-zq inklusive pricken zo; dess belopp S(z)är analytisk för z och S(z) = )(z) vid 0 z - zo R. Därför finns det en ändlig gräns lim )(z)\u003d Pm 5 (r) \u003d 5 (r) - Därför singularpunkten zq

Z->Zo Z-*Zo

disponibel. Teoremet har bevisats.

Kommentar. Det följer av beviset för satsen att i ett punkterat område 0 z - zo av en borttagbar singular punkt, funktionen F Z) sammanfaller med funktionen S(r), som är analytisk i hela grannskapet z - zo . Därför, om vi sätter /(th) = S(zq), sedan, utan att ändra funktionens värden F Z) när som helst i det punkterade området gör vi denna funktion analytisk i r, dvs. "ta bort" funktionen. Detta förklarar termen "borttagbar singularitet". Det är naturligt att betrakta sådana punkter som regelbundna och inte som singulära punkter i funktionen F Z).

Tänk till exempel på funktionen

I exempel 26.1 visades att Pm (n) = 1. d.v.s. singulära punkt

zq = 0 kan tas bort. Om vi ​​ställer in /i(0) = 1, eliminerar vi därigenom singulariteten och erhåller en funktion som är analytisk vid punkten zq = 0 (och i hela planet C).

Låt oss nu karakterisera polerna i termer av Laurent-expansioner.

Sats 26.3. En isolerad singularpunkt Zo för en funktion f(z) är en pol om och endast om, när huvuddelen av Laurent-expansionen med centrum Zq bara har ett ändligt antal distinkta

från nollkoefficienter med n:

Bevis. 1. Låt zq - pol, dvs. lim /( z) = oo.

Låt oss bevisa att Laurent expansion av funktionen F Z) har formen (2G.2). Sedan lim F Z)= oo. då finns det ett punkterat område av punkten

ki zq. vart i F Z)är analytisk och har inga nollor. Sedan funktionen g(z) = 1 /F Z) kommer också att vara analytisk i denna punkterade stadsdel, och lim g(z)= 0. Därför Zoär engångs *-? *0

singular punkt för funktionen g(z). Låt oss omdefiniera g(z) vid punkten zo, sätta g(zo)= 0. Sedan g(z) blir analytisk i hela området kring den (inte punkterade) punkten z 0 , och z0 kommer att vara dess isolerade noll. Beteckna med N multiplicitet (ordning) av denna nolla. Som visades i §23, i närheten av punkten zq funktion g(z) representeras i formen (se (23.2))

och (z$) f 0 och y>(z)är analytisk i något område av punkten zo- Därför att ip(z) kontinuerlig vid punkten zo och g>(zo) F 0" då ip(z) har inga nollor i någon omgivning av denna punkt heller. Därför funktion 1 /-p(z) kommer också att vara analytisk i det här området och expanderar därför i det i en Taylor-serie:

Genom att öppna parenteserna och ändra beteckningarna på koefficienterna skriver vi den sista expansionen i formuläret

där c_jv = 1> av f 0. Sålunda innehåller huvuddelen av Laurent-expansionen av f(r) endast ett ändligt antal termer; vi har kommit fram till erforderlig jämlikhet (26.2).

2. Släpp in en punkterad omgivning av en punkt th fungera )(z) representeras av Laurent-expansionen (26.2) (i en mer utökad form, se (26.3)), vars huvuddel endast innehåller ett ändligt antal termer, och Med- d" f 0. Det måste vi bevisa Zq - funktionsstolpe F Z). Multiplicera jämställdhet (26,3) med (G - G o) iV , vi får funktionen

Serien i (26.4) är en potensserie som konvergerar till en analytisk funktion inte bara i den punkterade, utan också i hela området kring punkten Zq. Därför funktionen h(z) blir analytisk i det här området om vi utökar det i th genom inställning h(zo)= s_dg f 0. Sedan

Således är punkten o en pol, och sats 26.3 är bevisad.

Multipel (ordning) av nollfunktionen g(z)= 1//(r) anropas polorder funktion /(r). Om en N- ordningen på stolpen är alltså th g(z)= (r - Zo)N ip(z), och gå) F 0, och, som visas i den första delen av beviset för sats 26.3, har expansionen av f(r) formen (26.3), där c_/v f 0. Omvänt, om f(r) expanderar till serien (26.3) och e-z F 0 då

t.s. N- ordningen på polen för funktionen f(r). På det här sättet, ordningen på zq-polen för funktionen/(G) är lika med talet på den ledande icke-nollkoefficienten för huvuddelen av Laurent-expansionen i det punkterade området för punkten zq(dvs lika med ett sådant nummer N, vad s_dg f 0 och sp= 0 vid P > N).

Låt oss bevisa följande påstående, vilket är bekvämt) för applikationer.

Följd 26.4. Punkten zq är en pol av ordning N av fiktionen/(G) om och endast om/(G) representera i formen

där h(z) är en analytisk funktion i närheten av en punkt th och h(zo)f 0.

Bevis. Fungera cp(z) = l/h(z)är analytisk i någon omgivning av punkten r. Villkoret i konsekvens 26.4 motsvarar följande:

Det är därför zq - multiplicitet noll N funktioner g(z). och därav multiplicitetspolen N funktioner /(2).

II exempel 26.5. Hitta isolerade singulära punkter för en funktion och bestämma deras typ.

D e u k tion n. Punkterna där (z 2 + 1 )(z+ H) 2 = 0. Om z 2 L- 1 = 0 sedan 2 = ±r om (z 4-H) 2 = 0, då z= -3. Därför har funktionen tre singulära punkter z= r, 22 = -r, Z3 = - 3. Överväg z:

G - första ordningens stolpe (vi använde Corollary 26.4). Det kan på liknande sätt bevisas att 22 = -jag också en stolpe av första ordningen. Under 2 timmar har vi:

Låt oss övergå till övervägandet av väsentligen singulara punkter.

Sats 26.6. En isolerad singularpunkt zq av en funktion f(z) är väsentligen singular om och endast om huvuddelen av Laurent-expansionen centrerad vid zq har oändligt många olika. noll, koefficienter med p.

Bevis. Sats 26.6 följer direkt av satser 26.2 och 26.3. Ja, om poängen zq är i huvudsak singular, då kan huvuddelen av Laurent-expansionen inte vara frånvarande eller innehålla ett ändligt antal termer (annars punkten Zq kommer att vara antingen avtagbar eller en stolpe). Därför måste antalet termer i huvuddelen vara oändligt.

Omvänt, om huvuddelen innehåller oändligt många medlemmar, då Zq kan varken vara en löstagbar punkt eller en stolpe. Följaktligen är denna punkt i huvudsak singular.

Enligt definitionen kännetecknas en väsentligen singular punkt av att funktionen f(2) varken har en ändlig eller oändlig gräns för z ->zq. En mer fullständig uppfattning om hur oregelbundet beteendet hos en funktion är i ett område av en väsentligen singulär punkt ges av följande sats.

Sats 26.7 (Sochockis sats). Om zq är väsentligen singular, då är punkten för funktionen f(z), sedan för vilket komplext tal som helst L, inklusive A = oj, det finns en sekvens av punkter z n så att z n -> zo och lim f(zn) = MEN.

n->os

Bevis. Tänk först på fallet A = oo. I den första delen av beviset för sats 2G.2 fastställde vi att if F Z)är avgränsad i någon punkterad omgivning av punkten r0, då är alla koefficienterna c, n = - 1, - 2,... av huvuddelen är lika med noll (och följaktligen är singulariteten i th borttagbar). Eftersom r0 enligt antagandet är en väsentligen singulär punkt, är funktionen f(r) obegränsad i varje punkterad omgivning av punkten r0. Låt oss ta några smala kvarter 0 Z så att f(zi) > 1 (om |/(r)| z - zo R/2 finns det en punkt z-2 , där |/(dd)| > 2, etc.: i det punkterade kvarteret O 71. Det är uppenbart att rn -e go och lim /(r«) = oo. Således, i fallet A = oo, sats 26.7

bevisat.

Låt nu A f oo. Antag först att det finns ett punkterat område 0

= -åå---- kommer att vara analytisk i detta punkterade område och följaktligen,

/(G) - MEN

följaktligen är r en isolerad singularispunkt för funktionen Φ(r). Låt oss visa. att r0 är en väsentligen singular punkt för Φ(r). Låt det vara fel. Då finns det en gräns lim Φ(r), antingen finit eller oändlig. Därför att

/(r) = A + , då finns Hsh /(r) också, vilket motsäger villkoret

F(g) ~ :-*z 0

syn på satsen. Således är r0 en väsentligen singular punkt för funktionen Φ(r). Enligt vad som bevisats ovan finns det en sekvens av punkter r n så att r n o och lim Φ(r n) = oo. Härifrån

Vi har bevisat det erforderliga påståendet under antagandet att f(r) F A i någon punkterad grannskap av punkten r. Låt oss nu anta att detta inte är sant, d.v.s. i varje godtyckligt liten punkterad omgivning av punkten där det finns en sådan punkt G", att f(r") = A. Sedan för någon P i det punkterade området 0 f(z u) = L. Således är det erforderliga påståendet sant P-juo

i alla fall, och sats 26.7 är bevisad.

Enligt (Sokhotskys) sats 26.7 tar funktionen f(r) värden godtyckligt nära vilket tal som helst i det utökade komplexa planet C i varje (godtyckligt liten) punkterad grannskap av en väsentligen singulär punkt.

För att studera isolerade singulära punkter är de välkända Taylor-expansionerna av grundläggande elementära funktioner ofta användbara.

EXEMPEL 2G.8. Bestäm typen av singularpunkt zq = 0 för funktionen

Löst och e. ​​Vi utökar täljaren och nämnaren i en Taylor-serie i potenser av r. Ersätter med (22.11) 3 z istället för r och subtrahera 1 får vi

Med hjälp av (22.12) får vi expansionen av nämnaren:

Serierna i dessa expansioner konvergerar i hela det komplexa planet €. Vi har

och /2(2) är analoga i närheten av punkten zo = 0 (och till och med i hela planet) och /2(20) F 0 då h(z)är också analytisk i någon omgivning av punkten gF 0. Enligt resultat 26.4 är punkten Zo = 0 är orderns pol N = 4.

II exempel 26.9. Hitta singulära punkter för en funktion F Z)= sin j - och bestäm deras typ.

P e in e och e. ​​Funktionen har en enda slutlig singularpunkt zq = 1. Vid andra punkter från C, funktionen w =--- analytisk; därav syndfunktionen w kommer att vara analytisk.

Substituering i expansionen av sinus (22.12) - istället för r får vi

Vi har erhållit expansionen av sin funktion i en Laurent-serie i en punkterad omgivning av punkten 20 = 1. Eftersom den resulterande expansionen innehåller oändligt många termer med negativa potenser (r - 1), så zq = 1 är en väsentlig singular punkt (i det här fallet består Laurent-expansionen endast av huvuddelen och den korrekta delen saknas).

Notera att det i detta fall också var möjligt att fastställa singularitetens natur direkt från definitionen, utan att tillgripa serieexpansion. Det finns faktiskt sekvenser (r") och (2") som konvergerar till zo= 1, och så att f(z" n)= 1, /(2") = 0 (ange sådana sekvenser själv). Så, F Z) har ingen gräns när z -> 1 och därav poängen zq - 1 är i huvudsak singular.

Låt oss introducera konceptet med en Laurent-expansion av en funktion i ett område av en punkt Zq = 00 och överväg sambandet mellan expansionen och singularitetens natur vid denna punkt. Observera att definitionerna av en isolerad singular punkt och dess typ (borttagbar, stolpe eller i huvudsak singular) överförs till höljet zq = oc oförändrad. Men satser 26.2. 26.3 och 26.6, relaterade till karaktären av Laurent-expansionerna, måste ändras. Poängen är att medlemmarna c n (z - 2o) sid. P= -1,-2,..., huvuddelen, definierar "'oregelbundenheten" för funktionen nära slutpunkten Zq, eftersom 2 tenderar att oo, kommer de att bete sig "korrekt" (tenderar till 0). Tvärtom, medlemmarna i den ordinarie delen med P= 1,2,... tenderar att oo; de bestämmer arten av singulariteten i Zq = oo. Därför kommer huvuddelen av expansionen i grannskapet av oo att vara villkoren med positiva krafter P, och korrekt - med negativ.

Låt oss introducera en ny variabel w = 12. Fungera tv= 1/2, utökad så att u(oo) = 0, en-till-en och konformt mappar grannskapet z > R poäng zq = 00 i närheten av |w| wq = 0. Om funktionen F Z) analyser i ett punkterat område R z Zq = oc, sedan funktionen G(w) = f(l/w) kommer att vara analytisk i det gula området 0 wo = 0. Eftersom det för 2 -> oo kommer att finnas w-> 0, alltså

Det är därför G(w) har vid punkten wq = 0 är en singularitet av samma typ som F Z) vid punkten Zq = 00. Låt oss expandera funktionen G(w) i en Laurent-serie i en punkterad omgivning av punkten wo = 0:

Summorna på höger sida av (26.5) representerar den korrekta respektive huvuddelen av expansionen. Låt oss gå vidare till variabeln z, ersätta w = 1/z:

betecknar P\u003d -A *, 6 * \u003d 6_ " \u003d med sid och märker det G(l/z) = F Z), vi får

Nedbrytningen (2G.G) kallas Laurent expansion av funktionen f(z) i en punkterad omgivning av punkten zq= oo. Den första summan i (2G.6) anropas höger del, och den andra summan är huvudsak denna nedbrytning. Eftersom dessa summor motsvarar de korrekta och huvudsakliga delarna av expansionen (26.5), uppfyller expansionen (26.6) analogerna till satserna 26.2, 26.3 och 26.6. Följande sats är således en analog till sats 26.2.

Sats 26.10. Isolerad singular punktZq - os (funktioner/(G) är borttagbar om och endast om Laurent-expansionen i ett punkterat område på denna punkt har formen

t.s. består av endast den korrekta delen.

Vi sätter /(oo) = co. Funktionen som definieras av serien (26.7) som konvergerar i grannskapet z > R poäng 2o \u003d oc, anropad analytisk vid punkten z o = oo. (Observera att denna definition är likvärdig med funktionens analyticitet G(w) vid punkten wo = 0.)

Exempel 26.11. Undersök singularpunkten zq = oo för funktionen

Eftersom gränsen är ändlig, alltså zo = oo är en borttagbar singularpunkt för funktionen f(r). Om vi ​​sätter /(oo) = lim J(z)= 0, alltså F Z) kommer att bli

tic vid punkt Zo= os. Låt oss visa hur man hittar motsvarande expansion (26.7). Låt oss gå vidare till variabeln w = 1 F Z. Ersätter z= 1 /?e, vi får

(den sista likheten är giltig i det punkterade området för punkten ww = 0, men vi kommer att utöka definitionen (7(0) = 0). Den resulterande funktionen har singulära punkter w =±jag, w =-1/3, och vid punkten Wq = 0 är analytisk. Expanderande funktion G(w) gradvis w(såsom gjordes i exempel 25.7) och substitution i den resulterande potensserien w = 1/z man kan erhålla expansionen (26.7) av funktionen F Z).

Sats 26.3 för fallet zo= oo kommer att skrivas om i följande form.

Sats 26.12. Isolerad singular punkt gå = oc funktion f(z) är en pol om och endast om huvuddelen av Laurent-expansionen (26.6) har endast ett ändligt antal koefficienter som inte är noll Med":

Här är serien den vanliga delen, och polynomet i parentes är huvuddelen av expansionen. Polens multiplicitet i oc definieras som polens multiplicitet wq = 0 funktioner G(z). Det är lätt att se att polens mångfald sammanfaller med talet N in (26,8).

Q p | (i 2 + 1) (z + 3) 2

En uppgift. Visa att funktionen F Z) =-- -- har in

punkt zo = oo polorder 3.

Sats 26.6 om en väsentlig singular punkt skrivs om för fallet zo= os nästan ordagrant, och vi uppehåller oss inte vid det i detalj.

Grundläggande begrepp och definitioner:

Nollan för den analytiska funktionen f(z) är punkten "a" för vilken f(a)=0.

Nollan i ordningen "n" för funktionen f(z) är punkten "a" om men fn(a)¹0.

En singularpunkt "a" kallas en isolerad singularpunkt för funktionen f(z) om det finns ett område till denna punkt där det inte finns några singularpunkter förutom "a".

Isolerade singulära punkter är av tre typer: .

1 avtagbara specialpunkter;

3 väsentliga singulära punkter.

Typen av en singularpunkt kan bestämmas baserat på beteendet hos en given funktion vid den hittade singularpunkten, såväl som från formen av Laurent-serien som erhålls för funktionen i närheten av den funna singularpunkten.

Bestämma typen av en singular punkt genom beteendet hos funktionen i den.

1. Avtagbara singulära punkter.

En isolerad singularpunkt a av funktionen f(z) kallas för borttagbar om det finns en ändlig gräns .

2. polare.

En isolerad singularpunkt a av funktionen f(z) kallas en pol if .

3. Betydande singulära punkter.

En isolerad singularpunkt a av en funktion f(z) kallas en väsentlig singularpunkt om varken finit eller oändlig existerar.

Följande relation äger rum mellan funktionens nollor och poler.

För att en punkt a ska vara en pol av ordningen n för funktionen f(Z), är det nödvändigt och tillräckligt att denna punkt är en noll av ordningen n för funktionen.

Om n=1 kallas polen enkel.

Definition: En isolerad singularpunkt med ett enskilt värde kallas:

a) kan tas bort om huvuddelen av nedbrytningen saknas;

b) en stolpe om huvuddelen innehåller ett begränsat antal medlemmar;

c) en väsentligen singulär punkt om huvuddelen innehåller ett oändligt antal termer.

a) Sålunda, i ett område med en borttagbar singular punkt, har expansionen formen:

den uttrycker funktionen vid alla punkter i cirkeln |z-a|

I mitten z=a är likheten falsk, eftersom funktionen vid z=a har en diskontinuitet, och den högra sidan är kontinuerlig. Om värdet på funktionen i mitten ändras och tar det lika med värdet på höger sida, kommer gapet att elimineras - därav namnet - borttagbart.

b) I närheten av en pol av ordning m har Laurent-seriens expansion formen:

c) I närheten av en enkel stolpe

Avdrag och formler för deras beräkning.

Resten av en analytisk funktion f(z) i en isolerad singularispunkt z 0 är ett komplext tal lika med värdet på integralen , taget i positiv riktning längs cirkeln L centrerad vid punkten z 0 , som ligger i analyticitetsområdet för funktionen f(z) (dvs. i ringen 0<|z-z0|

Återstoden av funktionen f(z) i en isolerad singularis punkt z 0 betecknas med symbolen Res f(z 0) eller Res (f(z); z 0). På det här sättet,

Resf(z0)= . (22.15.1)

Om vi ​​sätter n=-1 i formeln (22.15.1), får vi:

C-1=

eller Res f(z 0)= C-1,

de där. resten av funktionen f(z) med avseende på singularpunkten z 0 är lika med koefficienten för den första termen med en negativ exponent i expansionen av funktionen f(z) i en Laurent-serie.

Beräkning av avdrag.

Regelbundna eller borttagbara singulära punkter. Uppenbarligen, om z=z 0 är en regelbunden eller borttagbar singularpunkt för funktionen f(z), då Res f(z 0)=0 (det finns ingen huvuddel i Laurent-nedbrytningen i dessa fall, så c-1= 0).

Pol. Låt punkten z 0 vara en enkel pol för funktionen f(z). Då har Laurent-serien för funktionen f(z) i närheten av punkten z 0 formen:

Härifrån

Därför får vi genom att passera in denna likhet till gränsen som z --z 0

Upplösning f(z0)=

I grunden speciell punkt. Om punkten z 0 är en väsentligen singular punkt för funktionen f(z), så för att beräkna resten av funktionen vid denna punkt, bestämmer man vanligtvis direkt koefficienten c-1 i expansionen av funktionen i en Laurent-serie.

Händelseklassificering. Summa, produkt av händelser, deras egenskaper, grafisk representation.

Händelser är indelade i:

1. Slumpmässigt

2. Trovärdigt

3. Omöjligt

Pålitlig - detta är en händelse som nödvändigtvis inträffar under dessa förhållanden (natten följs av morgonen).

Slumpmässigt är en händelse som kan eller inte kan inträffa (godkänt ett prov).

Det omöjliga är en händelse som inte kommer att inträffa under de givna förhållandena (få ut en grön penna ur lådan med bara röda).