نقاط منفرد جدا شده نقاط منفرد جدا شده، طبقه بندی آنها

تعریف.نقطه مفرد تابع نامیده می شود جدا شده، اگر در برخی از همسایگان این نقطه یک تابع تحلیلی (یعنی تحلیلی در حلقه) باشد.

طبقه بندی نقاط منفرد جدا شده یک تابع به رفتار این تابع در همسایگی یک نقطه منفرد مربوط می شود.

تعریف.نقطه نامیده می شود قابل عرضه نقطه مفرد یک تابع اگر حد محدودی از این تابع در وجود داشته باشد.

مثال 5نشان دهید که تابع در یک نقطه دارای تکینگی قابل جابجایی است.

راه حل.با یادآوری اولین حد قابل توجه، محاسبه می کنیم

این بدان معنی است که تابع داده شده دارای یک تکینگی قابل جابجایی در نقطه است.

وظیفه 4.نشان دهید که نقطه برای قابل جابجایی است.

تعریف.نقطه نامیده می شود قطب تابع، اگر این تابع به طور نامحدود برای افزایش یابد، این است.

اجازه دهید به ارتباط بین مفاهیم صفر و قطب یک تابع تحلیلی توجه کنیم. بیایید تابع را به صورت .

اگر یک نقطه صفر ساده یک تابع باشد، آن تابع دارای یک قطب ساده است

اگر نقطه مرتبه صفر برای تابع باشد، برای تابع آن قطب است سفارش.

مثال 6نشان دهید که تابع در یک نقطه دارای قطب درجه سوم است.

راه حل.با فرض، دریافت می کنیم. همانطور که ما به سمت صفر گرایش داریم، طبق هر قانونی، داریم . سپس، و با آن خود تابع به طور نامحدود افزایش می یابد. بنابراین، یعنی نقطه مفرد یک قطب است. برای یک تابع، این نقطه به وضوح یک سه برابر صفر است. بنابراین، برای این تابع، نقطه یک قطب درجه سوم است.

وظیفه 5.نشان دهید که نقطه دارای یک قطب ساده است.

تعریف.نقطه نامیده می شود اساسا خاص نقطه تابع اگر در این نقطه نه محدود و نه حد نامتناهی تابع وجود داشته باشد (رفتار تابع تعریف نشده است).

اجازه دهید یک نقطه منفرد ضروری تابع باشد. سپس برای هر عدد مختلط از پیش تعیین شده، دنباله ای از نقاط همگرا وجود دارد که در امتداد آن مقادیر به: ( قضیه سوچوکی).

مثال 7نشان دهید که یک تابع در یک نقطه دارای تکینگی اساسی است.

راه حل.رفتار یک تابع معین را در مجاورت نقطه در نظر بگیرید. زیرا در امتداد قسمت مثبت محور واقعی (یعنی ) داریم و ; اگر در امتداد قسمت منفی محور واقعی (یعنی)، سپس و . بنابراین هیچ محدودیتی برای . طبق تعریف، یک تابع در یک نقطه دارای تکینگی اساسی است.

اجازه دهید رفتار تابع در صفر را از دیدگاه قضیه سوچوکی در نظر بگیریم. بگذارید هر عدد مختلطی غیر از صفر و بی نهایت باشد.

از برابری می یابیم . با فرض , ما دنباله ای از نقاط , . به طور مشخص، . در هر نقطه از این دنباله، تابع برابر است و بنابراین

وظیفه 6.نشان دهید که تابع در یک نقطه دارای تکینگی اساسی است.

یک نقطه در بی نهایت همیشه برای تابع خاص در نظر گرفته می شود. در صورتی که این تابع خارج از دایره ای که در مرکز مبدا قرار دارد، نقطه منفرد دیگری نداشته باشد، نقطه ای یک نقطه منفرد جدا شده از تابع نامیده می شود.

طبقه بندی نقاط منفرد جدا شده را نیز می توان به مورد تعمیم داد.

مثال 8نشان دهید که تابع در بی نهایت دارای دو قطب است.

راه حل.تابع را در نظر بگیرید که در آن یک تابع تحلیلی در همسایگی نقطه است و . این بدان معنی است که تابع در بی نهایت دارای یک صفر دو برابر است، اما برای تابع نقطه یک قطب دوگانه است.

مثال 9نشان دهید که تابع در بی نهایت دارای تکینگی اساسی است.

راه حل.مشکل مشابهی در pr.7 در نظر گرفته شده است. رفتار یک تابع را در همسایگی یک نقطه بی نهایت دور در نظر بگیرید. برای امتداد قسمت مثبت محور واقعی و برای امتداد قسمت منفی محور واقعی. این بدان معنی است که هیچ محدودیتی برای تابع در یک نقطه وجود ندارد و به موجب تعریف، این نقطه اساساً مفرد است.

ماهیت تکینگی یک تابع در یک نقطه قابل قضاوت است بخش اصلی گسترش لوران در همسایگی این نقطه.

قضیه 1.برای اینکه نقطه باشد قابل عرضه نقطه منفرد تابع، لازم و کافی است که بسط لوران مربوطه شامل قسمت اصلی نبود

وظیفه 6.با استفاده از بسط تیلور تابع در همسایگی نقطه، نشان دهید که تکینگی قابل جابجایی در صفر دارد.

قضیه 2.برای اینکه نقطه باشد قطب توابع، لازم و کافی است به طوری که بخش اصلی بسط لورن مربوطه شامل تعداد محدودی از اعضا بود :

تعداد بالاترین جمله منفی ترتیب قطب را تعیین می کند.

در این مورد، تابع را می توان به صورت نمایش داد

که در آن تابع تحلیلی در نقطه است، ترتیب قطب است.

مثال 10نشان دهید که تابع دارای قطب های ساده در نقاط است.

راه حل.یک نکته را در نظر بگیریم. ما از بسط Laurent این تابع در مجاورت این نقطه استفاده می کنیم که در مثال 2 به دست آمده است:

از آنجایی که بیشترین (و تنها) توان منفی در قسمت اصلی این بسط برابر با یک است، نقطه یک قطب ساده این تابع است.

این نتیجه را می شد از راه دیگری به دست آورد. اجازه دهید به شکل نمایش داده و قرار دهیم - این تابعی است که در نقطه و . از این رو، به دلیل (8) این تابع دارای یک قطب ساده در نقطه است.

راه دیگر: تابعی را در نظر بگیرید که یک صفر ساده در نقطه دارد. از این رو، در این نقطه دارای یک قطب ساده است.

به طور مشابه، اگر تابع را به شکل بنویسیم، که در آن یک تابع تحلیلی در نقطه است و، بلافاصله مشخص می شود که نقطه قطب ساده تابع است.

وظیفه 7.نشان دهید که تابع دارای یک قطب درجه 2 در نقطه و یک قطب از درجه 4 در نقطه است.

قضیه 3.برای اینکه نقطه باشد اساسا خاص نقطه تابع، لازم و کافی است که بخش اصلی گسترش لوران در محله ای از نقطه شامل تعداد نامتناهی عضو بود .

مثال 11.ماهیت تکینگی را در نقطه تابع تعیین کنید

راه حل.در بسط شناخته شده کسینوس، به جای زیر قرار می دهیم:

از این رو، بسط Laurent در همسایگی یک نقطه شکل دارد

در اینجا قسمت صحیح یک اصطلاح است. و قسمت اصلی شامل بی نهایت عبارت است، بنابراین نقطه اساساً مفرد است.

وظیفه 8.نشان دهید که در یک نقطه تابع دارای تکینگی اساسی است.

تابعی را در نظر بگیرید و بسط Laurent آن را در نقطه زیر بنویسید:

بیایید جایگزینی ایجاد کنیم، در حالی که نکته به سمت نقطه می رود. اکنون، در همسایگی یک نقطه در بی نهایت، داریم

باقی مانده است که یک نام جدید معرفی کنیم. ما گرفتیم

جایی که قسمت اصلی است و بخش منظم بسط لوران تابع در همسایگی یک نقطه بی نهایت دور است. بنابراین، در بسط لوران یک تابع در همسایگی یک نقطه، قسمت اصلی یک سری در توان های مثبت است، در حالی که قسمت صحیح یک سری در توان های منفی است. با در نظر گرفتن این

با این حال، معیارهای فوق برای تعیین ماهیت تکینگی برای یک نقطه بی نهایت دور معتبر باقی می مانند.

مثال 12.ماهیت تکینگی تابع را در نقطه پیدا کنید. ، سپس در یک نقطه ممکن است معلوم شود که منزوی نیست.

مثال 15تابع در یک نقطه بی نهایت دور دارای یک تکینگی اساسی است. نشان دهید که نقطه تابع یک نقطه منفرد مجزا نیست.

راه حل.این تابع دارای تعداد بی نهایت قطب در صفرهای مخرج است، یعنی در نقاط، . از آنجا که، پس نقطه، در هر همسایگی که قطب وجود دارد، نقطه حد برای قطب است.

مدل های توصیف شده توسط سیستم های دو معادله دیفرانسیل مستقل.

صفحه فاز پرتره فاز. روش ایزوکلاین ایزوکلین های اصلی ثبات حالت پایدار سیستم های خطی انواع نقاط کلیدی: گره، زین، فوکوس، مرکز. مثال: واکنش های شیمیایی مرتبه اول.

جالب ترین نتایج در مورد مدل سازی کیفی خواص سیستم های بیولوژیکی بر روی مدل های دو معادله دیفرانسیل به دست آمد که امکان مطالعه کیفی با استفاده از روش را فراهم می کند. صفحه فاز. سیستمی متشکل از دو معادله دیفرانسیل معمولی مستقل به شکل کلی را در نظر بگیرید

(4.1)

P(x،y)، Q(x،y)- توابع پیوسته تعریف شده در برخی از دامنه جیصفحه اقلیدسی ( x، y- مختصات دکارتی) و داشتن مشتقات پیوسته در این ناحیه که کمتر از اولی نباشد.

منطقه جیمی تواند نامحدود یا محدود باشد. اگر متغیرها x، yمعنای بیولوژیکی خاصی دارند (غلظت مواد، فراوانی گونه ها)، اغلب منطقه جیربع مثبت نیم صفحه سمت راست است:

0 £ ایکس< ¥ ,0 £ y< ¥ .

غلظت مواد یا فراوانی گونه ها را نیز می توان از بالا با حجم کشتی یا مساحت زیستگاه محدود کرد. سپس دامنه متغیرها به شکل زیر است:

0 £ ایکس< x 0 , 0 £ y< y 0 .

متغیرها x، yتغییر در زمان مطابق با سیستم معادلات (4.1)، به طوری که هر حالت از سیستم مطابق با یک جفت مقدار متغیر است. x، y).

برعکس، برای هر جفت متغیر ( x، y) مربوط به حالت خاصی از سیستم است.

صفحه ای را با محورهای مختصاتی در نظر بگیرید که مقادیر متغیرها بر روی آن رسم شده است x، y. هر نقطه ماین صفحه با حالت خاصی از سیستم مطابقت دارد. چنین صفحه ای صفحه فاز نامیده می شود و مجموع تمام حالات سیستم را نشان می دهد. نقطه M(x,y) نقطه نشان دهنده یا نشان دهنده نامیده می شود.

در زمان اولیه اجازه دهید t=t 0 نشان دهنده مختصات نقطه است م 0 (ایکس(تی 0)، y(تی 0)). در هر لحظه بعدی در زمان تینقطه تصویر با توجه به تغییرات مقادیر متغیرها حرکت می کند ایکس(تی)، y(تی). مجموعه ای از نقاط م(ایکس(تی)، y(t)) در صفحه فاز، که موقعیت آن با حالت های سیستم در فرآیند تغییر متغیرها در طول زمان مطابقت دارد. x(t), y(t)با توجه به معادلات (4.1)، نامیده می شود مسیر فاز

مجموعه مسیرهای فاز برای مقادیر مختلف اولیه متغیرها یک "پرتره" به راحتی قابل مشاهده از سیستم می دهد. ساختمان پرتره فازبه شما امکان می دهد در مورد ماهیت تغییرات در متغیرها نتیجه گیری کنید x، yبدون دانستن جواب های تحلیلی سیستم معادلات اولیه(4.1).

برای به تصویر کشیدن یک پرتره فاز، لازم است یک میدان برداری از جهت ها برای مسیرهای سیستم در هر نقطه از صفحه فاز ایجاد شود. با تعیین یک افزایشD t>0،افزایش های مربوطه را دریافت می کنیم D ایکسو D yاز عبارات:

D x=P(x,y)D تی,

D y=Q(x,y)D تی

جهت برداری dy/dxدر نقطه ( x، y) به علامت توابع بستگی دارد P(x، y)، Q(x، y)و با جدول قابل ارائه است:

P(x,y)>0,Q(x,y)>0
P(x,y)<0,Q(x,y)<0
P(x,y)>0,Q(x,y)<0
P(x,y)<0,Q(x,y)>0

.(4.2)

راه حل این معادله y=y(x، c), یا به طور ضمنی اف(x، y)=c،جایی که باثابت یکپارچگی است، خانواده منحنی های انتگرال معادله (4.2) را نشان می دهد - مسیرهای فازسیستم (4.1) در هواپیما x، y.

روش ایزوکلاین

برای ساخت یک پرتره فازی، فرد استفاده می کند روش ایزوکلاین -خطوطی بر روی صفحه فاز رسم می شوند که منحنی های انتگرال را در یک زاویه خاص قطع می کنند. معادله ایزوکلاین به راحتی از (4.2) بدست می آید. بگذاریم

جایی که ولی– ثابت معین معنی ولیمماس شیب مماس به مسیر فاز را نشان می دهد و می تواند مقادیر از -¥ به + ¥ . جایگزین کردن به جای dy/dxدر (4.2) مقدار ولیمعادله ایزوکلاین را بدست می آوریم:

.(4.3)

معادله (4.3) در هر نقطه از صفحه تنها مماس منحنی انتگرال مربوطه را تعیین می کند، به جز نقطه ای که در آن P(x,y)= 0، Q (x، y) = 0 ، که در آن جهت مماس نامعین می شود، زیرا مقدار مشتق نامشخص می شود:

.

این نقطه نقطه تقاطع همه خطوط همسان است - نکته ویژهبه طور همزمان مشتقات زمانی متغیرها را از بین می برد ایکسو y.

بنابراین، در نقطه منفرد، نرخ تغییر متغیرها برابر با صفر است. بنابراین، نقطه منفرد معادلات دیفرانسیل مسیرهای فاز (4.2) مطابق با حالت ساکن سیستم(4.1) و مختصات آن مقادیر ثابت متغیرها هستند x، y.

مورد توجه خاص هستند ایزوکلین های اصلی:

dy/dx=0، P(x، y)=0 – ایزوکلاین مماس های افقی و

dy/dx=¥ ، س(x، y)=0 – ایزوکلین مماس های عمودی

با ساخت همپایه های اصلی و یافتن نقطه تقاطع آنها (x,y) که مختصات آن شرایط را برآورده می کند:

بنابراین، نقطه تلاقی همه خطوط همسان صفحه فاز را خواهیم یافت، که در آن جهت مماس ها به مسیرهای فاز نامشخص است. آی تی - نقطه مفرد، که مطابقت دارد حالت ساکن سیستم(شکل 4.2).

سیستم (4.1) به تعداد نقاط تقاطع خطوط همسوی اصلی در صفحه فاز، حالت های ساکن دارد.

هر مسیر فاز مربوط به مجموعه‌ای از حرکات یک سیستم دینامیکی است که از حالت‌های یکسانی عبور می‌کند و تنها در آغاز مرجع زمانی با یکدیگر متفاوت است.

اگر شرایط قضیه کوشی برآورده شود، از طریق هر نقطه از فضا x، y، tاز یک منحنی انتگرال منفرد عبور می کند. همین امر، به لطف استقلال، برای مسیرهای فاز صادق است: یک مسیر فاز منحصر به فرد از هر نقطه از صفحه فاز عبور می کند.

ثبات حالت پایدار

بگذارید سیستم در حالت تعادل باشد.

سپس نقطه نماینده در یکی از نقاط منفرد سیستم قرار می گیرد که در آن طبق تعریف:

.

اینکه یک نقطه منفرد پایدار است یا نه، به این بستگی دارد که نقطه نماینده با یک انحراف کوچک از حالت ساکن خارج شود یا نه. همانطور که برای یک سیستم از دو معادله اعمال می شود، تعریف ثبات در زبانه, دبه شرح زیر است.

حالت تعادل پایدار است اگر برای هر ناحیه معینی از انحراف از حالت تعادل (ه )منطقه را می توان مشخص کرد د (ه )، احاطه به حالت تعادل و داشتن این خاصیت است که هیچ مسیری که در داخل منطقه شروع می شود د ، هرگز به مرز نمی رسد ه . (شکل 4.4)

برای یک کلاس بزرگ از سیستم ها - سیستم های خشن – ماهیت رفتاری که با یک تغییر کوچک در نوع معادلات تغییر نمی کند، اطلاعات مربوط به نوع رفتار در مجاورت حالت ساکن را می توان با مطالعه نه اصلی، بلکه ساده شده به دست آورد. خطی شدهسیستم.

سیستم های خطی

سیستمی متشکل از دو معادله خطی را در نظر بگیرید:

.(4.4)

اینجا آ ب پ ت- ثابت ها، x، y- مختصات دکارتی در صفحه فاز.

راه حل کلی به شکل زیر جستجو خواهد شد:

.(4.5)

این عبارات را در (4.4) جایگزین کرده و کاهش دهید ه ل تی:

(4.6)

سیستم جبری معادلات (4.6) با مجهولات الف، بفقط در صورتی جواب غیر صفر دارد که تعیین کننده آن که از ضرایب مجهولات تشکیل شده باشد برابر با صفر باشد:

.

با گسترش این تعیین کننده، معادله مشخصه سیستم را به دست می آوریم:

.(4.7)

حل این معادله مقادیر نشانگر را به دست می دهدل 1,2 ، که در آن مقادیر غیر صفر برای آنها امکان پذیر است آو براه حل های معادله (4.6). این مقادیر هستند

.(4.8)

اگر بیان رادیکال منفی باشد، پسل 1,2 اعداد مزدوج مختلط فرض کنید هر دو ریشه معادله (4.7) دارای اجزای واقعی غیر صفر هستند و هیچ ریشه چندگانه ای وجود ندارد. سپس جواب کلی سیستم (4.4) را می توان به صورت ترکیبی خطی از توان با توان نمایش داد.ل 1 , ل 2 :

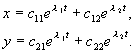(4.9)

برای تجزیه و تحلیل ماهیت مسیرهای احتمالی سیستم در صفحه فاز، ما استفاده می کنیم تبدیل مختصات همگن خطی،که سیستم را به شکل متعارف:

,(4.10)

که امکان نمایش راحت تری را در صفحه فاز در مقایسه با سیستم اصلی فراهم می کند (4.4). بیایید مختصات جدید را معرفی کنیمξ , η طبق فرمول های:

(4.1)

از درس جبر خطی معلوم می شود که اگر اجزای حقیقی برابر با صفر نباشندل 1 , ل 2 سیستم اصلی (4.4) با کمک تبدیلات (4.11) همیشه می تواند به شکل متعارف (4.10) تبدیل شود و رفتار آن در صفحه فاز بررسی شود.ξ , η . موارد مختلفی را که ممکن است در اینجا مطرح شود را در نظر بگیرید.

ریشه λ 1 , λ 2 - معتبر و با همان علامت

در این حالت، ضرایب تبدیل واقعی هستند، ما از صفحه واقعی حرکت می کنیمx، yبه صفحه واقعی ξ, η. با تقسیم دومی معادلات (4.10) بر اولی به دست می‌آییم:

.(4.12)

با ادغام این معادله، متوجه می شویم:

کجا .(4.13)

اجازه دهید با λ درک کنیم 2 ریشه معادله مشخصه با مدول بزرگ، که کلیت استدلال ما را نقض نمی کند. سپس، از آنجایی که در مورد مورد بررسی، ریشه λ 1 , λ2 - معتبر و با همان علامت،آ>1 ، و با منحنی های انتگرال از نوع سهمی روبرو هستیم.

همه منحنی های انتگرال (به جز محور η ، که مطابقت دارد ) در مبدا محور لمس کنید ξ, که منحنی انتگرالی معادله (4.11) نیز می باشد. مبدأ مختصات یک نقطه منفرد است.

حال اجازه دهید جهت حرکت نقطه نماینده در طول مسیرهای فاز را دریابیم. اگر λ 1، λ 2 منفی هستند، پس همانطور که از معادلات (4.10)، |ξ|، |η| مشاهده می شود در طول زمان کاهش می یابد. نقطه نشان دهنده به مبدأ نزدیک می شود، اما هرگز به آن نمی رسد. در غیر این صورت، این با قضیه کوشی، که می گوید فقط یک مسیر فاز از هر نقطه از صفحه فاز می گذرد، در تضاد است.

چنین نقطه منفردی که منحنی های انتگرال از آن عبور می کنند، درست مانند یک خانواده سهمی از مبدأ عبور می کند، یک گره نامیده می شود (شکل 2). 4.5)

حالت تعادل نوع گره در λ 1، λ 2 < 0 به گفته لیاپانوف پایدار است، زیرا نقطه نشان دهنده در امتداد تمام منحنی های انتگرال به سمت مبدا مختصات حرکت می کند. آی تی گره پایدار. اگر λ 1، λ 2 > 0، سپس |ξ|، |η| با گذشت زمان افزایش می یابد و نقطه نماینده از مبدأ دور می شود. در این مورد، نقطه مفرد– گره ناپایدار .

در صفحه فاز x، y ویژگی کیفی کلی رفتار منحنی های انتگرال باقی می ماند، اما مماس ها بر منحنی های انتگرال با محورهای مختصات منطبق نمی شوند. زاویه تمایل این مماس ها با نسبت ضرایب تعیین می شود α , β , γ , δ در معادلات (4.11).

ریشه λ 1 , λ 2 معتبر هستند و علائم مختلفی دارند.

تبدیل ازمختصات x، y به مختصات ξ, η دوباره واقعی معادلات متغیرهای متعارف دوباره شکل (4.10) دارند، اما اکنون علائم λ 1، λ 2 ناهمسان. معادله مسیر فاز شکل دارد:

کجا، (4.14)

با ادغام (4.14)، پیدا می کنیم

(4.15)

آی تی معادله خانواده ای از منحنی ها از نوع هذلولی را تعریف می کند که در آن هر دو محور مختصات هستندمجانبی هستند (در آ=1 ما خانواده ای از هذلولی های متساوی الساقین خواهیم داشت). محورهای مختصات نیز در این مورد منحنی های انتگرالی هستند– اینها تنها منحنی های انتگرالی خواهند بود که از مبدا عبور می کنند. هر یککه از سه مسیر فاز تشکیل شده است: دو حرکت به سمت حالت تعادل (یا دور شدن از حالت تعادل) و از حالت تعادل. تمام منحنی های انتگرال دیگر– هذلولی هایی هستند که از مبدأ عبور نمی کنند (شکل 2). 4.6) این نقطه مفرد نامیده می شود "زین اسب ». خطوط تراز نزدیک زین کوه مانند مسیرهای فاز در مجاورت زین رفتار می کنند.

اجازه دهید ماهیت حرکت نقطه نماینده در طول مسیرهای فاز نزدیک به حالت تعادل را در نظر بگیریم. اجازه دهید، برای مثال،λ 1 > 0، λ 2<0 . سپس نقطه نماینده بر روی محور قرار می گیرد ξ ، از مبدا دور می شود و روی محور قرار می گیرد η – به طور نامحدود به مبدأ مختصات نزدیک می شود, بدون رسیدن به آن در زمان محدود. هر جایی که نقطه نشان دهنده در لحظه اولیه باشد (به استثنای نقطه مفرد و نقاط مجانب η =0), در نهایت از حالت تعادل دور می شود، حتی اگر در ابتدا در امتداد یکی از منحنی های انتگرال به سمت یک نقطه منفرد حرکت کند..

بدیهی است که نقطه منفرد نوع زین همیشه ناپایدار است . فقط در شرایط اولیه انتخاب شده خاص روی مجانبη =0 سیستم به حالت تعادل نزدیک می شود. با این حال، این با این ادعا که سیستم ناپایدار است منافات ندارد. اگر حساب کنید, که همه حالت های اولیه سیستم در صفحه فاز به یک اندازه محتمل هستند، پس احتمال چنین حالت اولیه ای که مربوط به حرکت در جهت باشد.به نقطه مفرد برابر با صفر است. بنابراین هر حرکت واقعی سیستم را از حالت تعادل خارج می کند.بازگشت به مختصاتx,y,ما همان تصویر کیفی را از ماهیت حرکت مسیرها در اطراف مبدا دریافت می کنیم.

مرز بین موارد در نظر گرفته شده از یک گره و یک زین مورد استچه زمانی به عنوان مثال یکی از شاخص های مشخصه λ 1 , ناپدید می شود، که زمانی رخ می دهد که تعیین کننده سیستم باشد- اصطلاح adbc=0(به فرمول 4.8 مراجعه کنید ). در این حالت، ضرایب سمت راست معادلات (4.4) با یکدیگر متناسب هستند.:

و سیستم برای حالت های تعادل خود تمام نقاط خط را دارد:

منحنی های انتگرال باقی مانده خانواده ای از خطوط موازی با شیب هستند ، که در امتداد آن نقاط معرف بسته به علامت ریشه دوم معادله مشخصه λ یا به حالت تعادل نزدیک می شوند یا از آن دور می شوند. 2 = a+d.(شکل 4. 7 ) در این حالت مختصات حالت تعادل به مقدار اولیه متغیرها بستگی دارد.

ریشه λ 1 , λ 2 – مجتمعمزدوج

در این مورد، به طور واقعیایکسو yما خواهیم کرد مزدوج های پیچیده دارند ξ , η (4.10) . با این حال، با معرفی یک تبدیل میانی دیگر، در این مورد نیز امکان کاهش در نظر گرفتن به یک تبدیل همگن خطی واقعی وجود دارد. بگذاریم:

(4.16)

جایی که الف، ب،و u، v – ارزش های واقعی می توان نشان داد که تحول ازx، yبه u، v بر اساس فرضیات ما، واقعی، خطی، همگن با یک تعیین کننده غیر صفر است. با توجه به معادلات(4.10، 4.16) داریم:

جایی که

(4.17)

تقسیم دومی از معادلات بر اولی، ما گرفتیم:

که ادغام آن راحت تر است, اگر به سیستم مختصات قطبی سوئیچ کنیم (r φ ) . بعد از تعویضاز کجا می گیریم:

.(4.18)

بنابراین، در صفحه فازu، vما با خانواده ای از مارپیچ های لگاریتمی سر و کار داریم که هر کدام داراینقطه مجانبی در مبدانقطه منفرد که نقطه مجانبی تمام منحنی های انتگرال است که شکل مارپیچی دارند, دوست تو در تودوست، زنگ زد تمرکز ( شکل 4.8 ) .

اجازه دهید ماهیت حرکت نقطه نشان دهنده در طول مسیرهای فاز را در نظر بگیریم. ضرب اول معادله (4.17) درتو، و دوم به vو با اضافه کردن، دریافت می کنیم:

جایی که

اجازه دهید آ 1 < 0 (آ 1 = Reλ ) . سپس نقطه نشان دهنده به طور پیوسته به مبدأ نزدیک می شود بدون اینکه در زمان محدودی به آن برسد. این بدان معنی است که مسیرهای فاز مارپیچ های پیچشی هستند و با نوسانات میرا مطابقت دارند.متغیرها آی تی - تمرکز ثابت .

در مورد یک تمرکز پایدار، مانند یک گره پایدار، نه تنها شرط لیاپانوف برآورده می شود، بلکه یک نیاز دقیق تر نیز وجود دارد. یعنی برای هر گونه انحراف اولیه، سیستم در نهایت تا حد مطلوب به موقعیت تعادل باز می گردد. چنین ثباتی که در آن انحرافات اولیه نه تنها افزایش نمی یابد، بلکه زوال می یابد و به سمت صفر می رود، نامیده می شود. ثبات مطلق .

اگر در فرمول (4.18) آ 1 >0 ، سپس نقطه نشان دهنده از مبدا دور می شود و ما با آن سروکار داریم تمرکز ناپایدار . هنگام حرکت از هواپیماu، vبه صفحه فازایکس, yمارپیچ ها نیز مارپیچی باقی می مانند، اما تغییر شکل می دهند.

اکنون موردی را در نظر بگیرید کهآ 1 =0 . مسیرهای فاز در هواپیماu، vحلقه هایی وجود خواهد داشت که در هواپیماx، yبیضی های مناسب:

بنابراین، دریک 1=0 از طریق یک نقطه خاصx= 0,y= 0 هیچ منحنی انتگرالی عبور نمی کند. چنین نقطه منفرد ایزوله ای که در نزدیکی آن منحنی های انتگرال منحنی های بسته هستند، به ویژه بیضی هایی که در یکدیگر تعبیه شده اند و نقطه منفرد را محصور می کنند، مرکز نامیده می شود.

بنابراین، بسته به ماهیت ریشه های معادله مشخصه (4.7)، شش نوع تعادل ممکن است. نمایی از مسیرهای فاز در هواپیما x، yبرای این شش مورد در شکل نشان داده شده است. 4.9.

برنج. 4.9.انواع پرتره های فاز در همسایگی حالت ساکن برای سیستم معادلات خطی (4.4).

پنج نوع حالت تعادل خشن هستند، ماهیت آنها با تغییرات به اندازه کافی کوچک در سمت راست معادلات تغییر نمی کند (4.4). در این مورد، تغییرات نه تنها در سمت راست، بلکه در مشتقات مرتبه اول آنها نیز باید کوچک باشد. ششمین حالت تعادل - مرکز - درشت نیست. با تغییرات کوچک در پارامترهای سمت راست معادلات، به یک کانون پایدار یا ناپایدار می رود.

نمودار انشعاب

اجازه دهید نماد را معرفی کنیم:

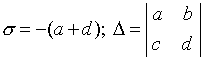. (4.11)

سپس معادله مشخصه را می توان به شکل زیر نوشت:

. (4.12)

صفحه ای را با مختصات دکارتی مستطیلی در نظر بگیرید س , D و مناطق مربوط به یک نوع حالت تعادل را که با ماهیت ریشه های معادله مشخصه تعیین می شود، روی آن علامت بزنید.

.(4.13)

شرط پایداری حالت تعادل، وجود قسمت واقعی منفی y خواهد بودل 1 و ل 2 . شرط لازم و کافی برای این امر تحقق نابرابری هاستس > 0, D > 0 . در نمودار (4.15)، این شرایط مربوط به نقاط واقع در ربع اول صفحه پارامتر است. نقطه مفرد کانون اگرل 1 و ل 2 مجتمع این شرایط مربوط به نقاطی از هواپیما است که برای آنها , آن ها نقاط بین دو شاخه سهمیس 2 = 4 D. نقاط نیمه محوری س = 0, D> 0، مربوط به حالت های تعادل از نوع مرکز است. به همین ترتیب،ل 1 و ل 2 - نشانه های معتبر، اما متفاوت، یعنی. نقطه مفرد یک زین خواهد بود اگر D<0, و غیره. در نتیجه، نمودار پارتیشن صفحه پارامتر را دریافت می کنیم س, D، به مناطق مربوط به انواع مختلف حالت های تعادلی.

برنج. 4.10.نمودار انشعاب

برای سیستم معادلات خطی 4.4

اگر ضرایب سیستم خطی آ ب پ تبه برخی از پارامترها بستگی دارد، سپس هنگامی که این پارامتر تغییر می کند، مقادیر نیز تغییر می کندس , D . هنگام عبور از مرزها، ماهیت پرتره فاز به طور کیفی تغییر می کند. بنابراین، چنین مرزهایی را مرزهای انشعاب می نامند - در طرف مقابل مرز، سیستم دارای دو پرتره فاز متفاوت از نظر توپولوژیکی و بر این اساس، دو نوع رفتار متفاوت است.

نمودار نشان می دهد که چگونه چنین تغییراتی می تواند رخ دهد. اگر موارد خاص - مبدا مختصات - را حذف کنیم، به راحتی می توان دید که زین می تواند در هنگام عبور از محور y به یک گره، پایدار یا ناپایدار برود. یک گره پایدار می تواند به یک زین یا یک کانون پایدار و غیره حرکت کند. توجه داشته باشید که گره پایدار-فوکوس پایدار و گره ناپایدار-گره ناپایدار انتقال کانون دو شاخه ای نیستند، زیرا توپولوژی فضای فاز در این مورد تغییر نمی کند. ما با جزئیات بیشتری در مورد توپولوژی فضای فاز و انتقال دوشاخه در سخنرانی 6 صحبت خواهیم کرد.

تحت انتقال دوشاخه، ماهیت پایداری نقطه منفرد تغییر می کند. به عنوان مثال، یک فوکوس پایدار از طریق مرکز می تواند به یک تمرکز ناپایدار تبدیل شود. این انشعاب نامیده می شود انشعاب آندرونوف-هوپفبا نام دانشمندانی که آن را مطالعه کردند. با این انشعاب در سیستم های غیر خطی، یک سیکل حدی ایجاد می شود و سیستم خود نوسان می شود (به سخنرانی 8 مراجعه کنید).

مثال. سیستم واکنش های شیمیایی خطی

ماده ایکساز خارج با سرعت ثابت به داخل جریان می یابد، به ماده Y و با سرعتی متناسب با غلظت ماده تبدیل می شود. Y، از کره واکنش خارج می شود. همه واکنش ها درجه اول هستند، به استثنای هجوم ماده از بیرون که مرتبه صفر دارد. طرح واکنش به نظر می رسد:

(4.14)

و توسط سیستم معادلات توصیف می شود:

(4.15)

غلظت های ثابت را با مساوی کردن ضلع های سمت راست با صفر بدست می آوریم:

.(4.16)

پرتره فاز سیستم را در نظر بگیرید. اجازه دهید معادله دوم سیستم (4.16) را بر معادله اول تقسیم کنیم. ما گرفتیم:

.(4.17)

معادله (4.17) رفتار متغیرها را در صفحه فاز تعیین می کند. اجازه دهید یک پرتره فازی از این سیستم بسازیم. ابتدا ایزوکلین های اصلی را روی صفحه فاز رسم می کنیم. معادله ایزوکلاین مماس های عمودی:

معادله ایزوکلاین مماس های افقی:

نقطه منفرد (حالت ایستا) در تقاطع همسطحهای اصلی قرار دارد.

حال اجازه دهید تعیین کنیم که محورهای مختصات در چه زاویه ای منحنی های انتگرال را قطع می کنند.

اگر یک x= 0، سپس .

بنابراین، مماس شیب مماس بر منحنی های انتگرال y=y(x)،عبور از محور y x=0، در نیم صفحه بالا منفی است (به یاد بیاورید که متغیرها x، yدارای مقادیر غلظت هستند و بنابراین ما فقط به ربع سمت راست بالای صفحه فاز علاقه مندیم). در این حالت مقدار مماس زاویه میل مماس با فاصله از مبدا افزایش می یابد.

محور را در نظر بگیرید y= 0. در تقاطع این محور، منحنی های انتگرال با معادله توصیف می شوند

در مماس شیب منحنی های انتگرالی که از محور آبسیسا عبور می کنند مثبت است و با افزایش از صفر تا بی نهایت افزایش می یابد. ایکس.

در .

سپس، با افزایش بیشتر، مماس شیب در مقدار مطلق کاهش می‌یابد، منفی باقی می‌ماند و به 1- میل می‌کند. ایکس ® ¥ . با دانستن جهت مماس ها به منحنی های انتگرال روی همسطح های اصلی و روی محورهای مختصات، می توان تصویر کامل مسیرهای فاز را ساخت.

ماهیت پایداری نقطه منفرد با استفاده از روش لیاپانوف مشخص خواهد شد. تعیین کننده مشخصه سیستم به شکل زیر است:

.

با گسترش دترمینان، معادله مشخصه سیستم را به دست می آوریم: ، یعنی ریشه های معادله مشخصه هر دو منفی هستند. بنابراین، حالت ساکن سیستم یک گره پایدار است. در همان زمان، غلظت ماده ایکستمایل به حالت ساکن همیشه یکنواخت دارد، غلظت ماده Y می تواند از حداقل یا حداکثر عبور کند. رژیم های نوسانی در چنین سیستمی غیرممکن است.

سری تیلور به عنوان ابزاری موثر برای مطالعه توابع تحلیلی در دایره zol عمل می کند. فرمی که بسط های تیلور را تعمیم می دهد. سری (1) که به عنوان مجموع دو سری شناخته می شود، سری Laurent نامیده می شود. واضح است که ناحیه همگرایی سری (1) قسمت مشترک نواحی همگرایی هر یک از سری (2) است. بیا پیداش کنیم مساحت همگرایی سری اول دایره ای است که شعاع آن با فرمول کوشی-هادامارد در داخل دایره همگرایی، سری (3) به یک تابع تحلیلی همگرا می شود و در هر دایره ای با شعاع کوچکتر، به طور مطلق همگرا می شود. و به صورت یکنواخت سری دوم یک سری توان نسبت به متغیر است.سری (5) در دایره همگرایی خود به تابع تحلیلی متغیر مختلط m-*oo همگرا می شود و در هر دایره ای با شعاع کوچکتر به طور مطلق و یکنواخت همگرا می شود. به این معنی که ناحیه همگرایی سری (4) ظاهر دایره است - اگر یک ناحیه مشترک همگرایی سری (3) و (4) وجود دارد - یک حلقه دایره ای که در آن سری (1) به یک تابع تحلیلی همگرا می شود. علاوه بر این، در هر حلقه، به طور مطلق و یکنواخت همگرا می شود. مثال 1. تعیین منطقه همگرایی سری راد لورن نقاط منفرد جدا شده و طبقه بندی آنها (z) که در یک حلقه دایره ای تک مقداری و غیر سیاسی است، می توان در این حلقه به صورت مجموع یک سری همگرا که ضرایب آن را نشان داد. Cn به طور منحصر به فرد توسط فرمول هایی تعیین و محاسبه می شود که در آن 7p دایره ای با شعاع m است. اجازه دهید یک نقطه دلخواه z را در داخل حلقه R ثابت کنیم. دایره هایی با مراکزی در نقطه r می سازیم که شعاع های آنها نابرابری ها را برآورده می کند و حلقه جدیدی را در نظر می گیریم.طبق قضیه انتگرال کوشی برای یک دامنه به هم پیوسته، داریم برای تمام نقاط £ در امتداد دایره 7d*، رابطه مجموع یک سری همگرای یکنواخت 1 1 برقرار است. بنابراین، کسری ^ را می توان به صورت vi- /" / به روشی متفاوت، برای همه نقاط ξ در نشان داد. دایره ir> ما رابطه داریم بنابراین، کسر ^ را می توان به عنوان مجموع یک سری همگرای یکنواخت در فرمول های (10) و (12) توابع تحلیلی در یک حلقه دایره ای نشان داد. بنابراین، بر اساس قضیه کوشی، اگر دایره های 7/r و 7r/ با هر دایره ای جایگزین شوند، مقادیر انتگرال های مربوطه تغییر نمی کند. این به ما اجازه می دهد تا فرمول های (10) و (12) را با هم ترکیب کنیم.با جایگزینی انتگرال های سمت راست فرمول (8) به ترتیب با عبارت های (9) و (11) آنها بسط مورد نظر را بدست می آوریم.از آنجایی که z یک دلخواه است. از نقطه حلقه، نتیجه می شود که سری (14) در همه جای این حلقه به تابع f(z) همگرا می شود و در هر حلقه ای این سری به طور مطلق و یکنواخت به این تابع همگرا می شود. اجازه دهید اکنون ثابت کنیم که تجزیه شکل (6) منحصر به فرد است. فرض کنید که یک تجزیه دیگر اتفاق بیفتد سپس در همه جای حلقه R، در محیط، سری (15) به طور یکنواخت همگرا می شوند. هر دو طرف برابری را ضرب کنید (که m یک عدد صحیح ثابت است، و هر دو سری را به صورت ترم ادغام کنید. در نتیجه، در سمت چپ و در سمت راست - Csh قرار می گیریم. بنابراین، (4, \u003d St. m یک عدد دلخواه است، سپس آخرین سری برابری (6) که ضرایب آن با فرمول (7) محاسبه می شود، سری Laurent تابع f(z) در حلقه 7 نامیده می شود) برای ضرایب سری Laurent به ندرت در عمل استفاده می شود، زیرا، به عنوان یک قاعده، آنها به محاسبات دست و پا گیر نیاز دارند. معمولاً، در صورت امکان، از بسط های آماده تیلور از توابع ابتدایی استفاده می شود. بر اساس منحصر به فرد بودن بسط، هر روش قانونی منجر به همان نتیجه می شود. مثال 2 بسط های سری Laurent توابع دامنه های مختلف را در نظر بگیرید، با این فرض که Fuiscius /(r) دارای دو نقطه منفرد است: بنابراین، سه حوزه حلقه وجود دارد. و در مرکز نقطه r = 0. که در هر کدام تابع f(r) تحلیلی است: الف) دایره بیرون دایره است (شکل 27). اجازه دهید بسط های Laurent تابع /(z) را در هر یک از این مناطق پیدا کنیم. ما /(z) را به عنوان مجموع کسرهای ابتدایی نشان می دهیم a) رابطه تبدیل دایره (16) را به صورت زیر با استفاده از فرمول مجموع عبارت های یک پیشروی هندسی، به دست می آوریم. ب) حلقه تابع -z در این حلقه همگرا باقی می ماند، زیرا سری (19) برای تابع j^j برای |z| > 1 واگرا می شود. بنابراین، تابع /(z) را به صورت زیر تبدیل می کنیم: با اعمال فرمول (19) دوباره، به دست می آوریم که این سری برای همگرا می شود. با جایگزینی بسط (18) و (21) به رابطه (20)، ج) بیرونی دایره برای تابع -z با |z| > 2 واگرا می شود و سری (21) برای تابع اجازه دهید تابع /(z) را به شکل زیر نمایش دهیم: /<*> با استفاده از فرمول های (18) و (19)، OR 1 را به دست می آوریم. این مثال نشان می دهد که برای همان تابع f(z) بسط Laurent، به طور کلی، شکل متفاوتی برای حلقه های مختلف دارد. مثال 3. تجزیه سری 8 Laurent تابع سری Laurent نقاط منفرد جدا شده و طبقه بندی آنها در ناحیه حلقوی A را بیابید ما از نمایش تابع f (z) به شکل زیر استفاده می کنیم: و عبارت دوم را با استفاده از فرمول برای مجموع عبارات یک تصاعد هندسی، با جایگزینی عبارات یافت شده در فرمول (22)، مثال 4 را به دست می آوریم. تابع را در یک سری Laurent در همسایگی zq نازک = 0 بسط می دهیم. برای هر یک پیچیده اجازه دهید این بسط برای هر نقطه z Ф 0 معتبر است. در این حالت، ناحیه حلقوی کل صفحه مختلط با یک نقطه پرتاب شده z - 0 است. این ناحیه را می توان با رابطه زیر تعریف کرد: این تابع تحلیلی است. در منطقه از فرمول (13) برای ضرایب سری Laurent، با همان استدلال پاراگراف قبل، می توان نابرابری های Kouiw را به دست آورد. اگر تابع f(z) روی یک دایره محدود شده باشد، جایی که M یک ثابت است، اگر یک همسایگی حلقوی نقطه وجود داشته باشد، نقطه zo یک نقطه منفرد جدا شده از تابع f(z) نامیده می شود. گاهی اوقات به این مجموعه، محله سوراخ شده نقطه 2o نیز می گویند، که در آن تابع f(z) تک مقداری و تحلیلی است. در خود نقطه zo تابع یا تعریف نشده است یا تک ارزشی و تحلیلی نیست. سه نوع نقطه منفرد بسته به رفتار تابع /(z) هنگام نزدیک شدن به نقطه zo متمایز می شوند. به یک نقطه منفرد جدا شده گفته می شود: 1) اگر یک نقطه محدود وجود داشته باشد قابل جابجایی است 2) اگر یک نقطه pmusach وجود داشته باشد 3) اگر تابع f(z) محدودیتی برای آن نداشته باشد، یک نقطه اساساً منفرد است. قضیه 16. یک نقطه مفرد جدا شده z0 تابع f(z) یک نقطه مفرد قابل جابجایی است اگر و فقط اگر بسط لورن تابع f(z) در همسایگی نقطه zo شامل قسمت اصلی نباشد، به عنوان مثال، دارای شکل Let zo - نقطه منفرد قابل جابجایی است. سپس یک تابع متناهی وجود دارد، بنابراین، تابع f(z) در یک همسایگی پروکولوژیک نقطه r محدود می شود. ما به واسطه نابرابری های کوشی تنظیم می کنیم از آنجایی که می توان p را به طور دلخواه کوچک انتخاب کرد، پس همه ضرایب در توان های منفی (z - 20) برابر با صفر هستند: برعکس، اجازه دهید Laurent بسط تابع /(r) در همسایگی نقطه zq فقط قسمت صحیح را داشته باشد، یعنی شکل (23) دارد و بنابراین، تیلور است. به راحتی می توان فهمید که برای z -* z0 تابع /(r) مقدار حدی دارد: قضیه 17. یک نقطه منفرد zq از تابع f(z) قابل جابجایی است اگر و فقط اگر تابع J(z) باشد. محدود در برخی از محله های سوراخ شده نقطه zq، Zgmechai نیست. فرض کنید r0 یک نقطه منفرد قابل جابجایی f(r) باشد. با فرض اینکه تابع f(r) در یک دایره که مرکز آن نقطه th است تحلیلی است. این نام نقطه را مشخص می کند - یکبار مصرف. قضیه 18. نقطه منفرد zq تابع f(z) قطب است اگر و فقط اگر بخش اصلی بسط لوران تابع f(z) در همسایگی نقطه دارای یک عدد متناهی (و مثبت) باشد. از عبارات غیر صفر، یعنی به شکل 4 است. بگذارید z0 یک قطب باشد. از آن زمان یک همسایگی سوراخ شده از نقطه z0 وجود دارد که در آن تابع f(z) تحلیلی و غیر صفر است. سپس یک تابع تحلیلی در این همسایگی تعریف می شود و از این رو، نقطه zq یک نقطه منفرد قابل جابجایی (صفر) تابع است یا در جایی که h(z) یک تابع تحلیلی است، h(z0) ∩ 0. تحلیلی در همسایگی است. نقطه zq، و از این رو، از آنجا به دست می آوریم که اجازه دهید فرض کنیم که تابع f(z) دارای تجزیه شکل (24) در یک محله سوراخ شده از نقطه zo است. یعنی در این همسایگی تابع f(z) همراه با تابع تحلیلی است. برای تابع g(z)، بسط معتبر است که از آن مشخص است zq یک نقطه منفرد قابل جابجایی تابع g(z) است و وجود دارد سپس تابع به سمت 0 میل می کند - قطب تابع یک ساده دیگر وجود دارد. حقیقت. نقطه Zq قطبی از تابع f(z) است اگر و فقط اگر تابع g(z) = y را بتوان با تنظیم g(z0) = 0 به یک تابع تحلیلی در همسایگی نقطه zq گسترش داد. از قطب تابع f(z) مرتبه صفر تابع jfa نامیده می شود. قضایای 16 و 18 بر ادعای زیر دلالت دارند. قضیه 19. یک نازک منفرد جدا شده اساساً مفرد است اگر و فقط در صورتی که بخش اصلی انبساط لوران در همسایگی سوراخ شده این نقطه حاوی بی‌نهایت عبارات غیرصفر باشد. مثال 5. نقطه مفرد تابع zo = 0 است. ما نقاط منفرد جدا شده از سری Laurent و طبقه بندی آنها را داریم بنابراین، zo = 0 یک نقطه منفرد قابل جابجایی است. بسط تابع /(z) در یک سری لوران در مجاورت نقطه صفر فقط شامل قسمت صحیح است: مثال 7. f(z) = نقطه مفرد تابع f(z) zq = 0 است. رفتار این تابع را روی محورهای واقعی و فرضی در نظر بگیرید: در محور واقعی در x 0، در محور فرضی بنابراین، نه محدود و نه محدود حد بی نهایت f(z) در z -* 0 وجود ندارد. از این رو نقطه r0 = 0 یک نقطه اساساً منفرد تابع f(z) است. اجازه دهید بسط لورن تابع f(z) را در همسایگی نقطه صفر پیدا کنیم. برای هر C پیچیده ای که داریم تنظیم می کنیم. سپس بسط Laurent شامل تعداد نامتناهی عبارت با توان منفی z است.

اجازه دهید zq - نقطه مفرد تابع f(z)، t.s. f(z)اما در این مرحله تحلیلی است (به ویژه، ممکن است در آن تعریف نشود). اگر چنین محله سوراخ شده ای از نقطه وجود داشته باشد zq (یعنی مجموعه O z - پس zq f(z) آلیاتیک است zoتماس گرفت نقطه منفرد جدا شدهکارکرد f(z).این تعریف در مورد نیز حفظ شده است zn =اوه، اگر ید محله سوراخ شده یک نقطه باشد zq = oo مجموعه را درک کنید z >من - ظاهر یک دایره در مرکز مبدا. به عبارت دیگر، نقطه مفرد به zq منزوی گفته می شود اگر همسایگی این نقطه وجود داشته باشد که در آن نقاط مفرد دیگری متفاوت از آن وجود داشته باشد. zq در همه جای زیر، ما فقط نقاط مفرد یک کاراکتر تک ارزشی را در نظر می گیریم (تابع f(z)منحصر به فرد فرض می شود).

بسته به رفتار تابع f(z)در z -> zqسه نوع نقطه مفرد وجود دارد. نقطه منفرد جدا شده توابع zq f(z)به نام:

1) نقطه منفرد قابل جابجاییاگر حد محدودی وجود دارد

2) قطباگر محدودیتی وجود دارد

3) نکته ضروری،اگر f(z) نه محدود دارد و نه حد نامتناهی برای z-> zq.

مثال 26.1. اجازه دهید نشان دهیم که هر سه نوع نقطه مفرد تحقق یافته است. در نظر گرفتن f(ز)= نقطه zq = 0 جدا شده است

نقطه منفرد این تابع با استفاده از فرمول (22.12)، بسط را بدست می آوریم

که از آن نتیجه می شود که محدودیت وجود دارد fi(z)= 1. بنابراین zq = 0 است

یک نقطه منفرد قابل جابجایی تابع است fi(z).

عملکرد f'j(z) =--- یک قطب در یک نقطه دارد zo= 1 زیرا

2 r" ایکس

اکنون تابع را در نظر بگیرید )z(z)= e 1 ^ r و نشان دهید که زو = O یک نقطه مفرد ضروری این تابع است. هنگام تلاش zبه صفر در امتداد محور واقعی، حد چپ و راست تابع f (ز)متفاوت: لیم با 1 / 1 = 0، لیم با 1 /* =سیستم عامل این دلالت می کنه که،

x->0-0 x->0+O

چی f:i(z)برای 2 نه محدود و نه حد نامحدود دارد -> اوه، یعنی zq = 0 یک نقطه اساساً منفرد این تابع است. (توجه داشته باشید که با توجه به موضوع z-iyبه صفر در تابع محور فرضی

اصلا محدودیت نداره.)

البته، نقاط مفرد غیر ایزوله نیز وجود دارد. مثلا. تابع در نقاط دارای قطب است z n = -, پ= ± 1، ± 2، ...

در نتیجه، Zq = 0 یک نقطه منفرد غیر ایزوله از این تابع است: در هر همسایگی (به طور خودسرانه کوچک) این نقطه نقاط منفرد دیگری وجود دارد. g ص.

اجازه دهید زو-نقطه مفرد جدا شده نهایی یک تابع f(z).سپس f(z)در برخی از محله های سوراخ شده 0 Zo از نقطه مشابه است zoاین همسایگی را می توان به عنوان حلقه ای با شعاع داخلی r = 0 در نظر گرفت. با قضیه 25.1، در همسایگی مورد بررسی، تابع f(z)را می توان در یک سری Laurent (25.2) گسترش داد. ما نشان خواهیم داد که رفتار تابع برای 2 -> zq (یعنی نوع نقطه مفرد زو)بستگی به شکل قسمت اصلی تجزیه دارد (25.2). این شرایط منشأ اصطلاح "قسمت اصلی" را توضیح می دهد.

قضیه 2G.2. یک نقطه منفرد zo یک تابع f(z) قابل جابجایی است اگر و فقط اگر بسط Lorap در همسایگی سوراخ شده این نقطه دارای oid باشد.

آن ها فقط از قسمت صحیح تشکیل شده است, و تمام ضرایب قسمت اصلی با گلوله برابر است.

اثبات 1. اجازه دهید zoیک نقطه منفرد قابل جابجایی است. اجازه دهید ثابت کنیم که بسط Laurent تابع f(z)دارای فرم (26.1) می باشد. از آنجایی که نقطه مفرد zoقابل جابجایی است، پس یک محدودیت محدود وجود دارد f(z) = A.در نتیجه، f(z)محدود در محله سوراخ شده 0 z - zq نقطه زو،آن ها )(ز) برای همه zاز این محله هر کدام را بگیرید آر. U р /?|، و از فرمول (25.3) برای ضرایب سری Laurent استفاده کنید:

برای ضرایب بخش اصلی بسط n =- 1,-2,... برای چنین مقادیری پما داریم p~n-e 0 در آر-> 0. از آنجایی که مقدار آرپس از آن می توان خودسرانه کوچک انتخاب کرد آقای ~"می تواند خودسرانه کوچک باشد. از آنجایی که |c t,| ^ آقای ~ nو cn به p بستگی ندارد، سپس cn = 0 برای و= - 1، -2،... که قرار بود ثابت شود.

2. اکنون فرض می کنیم که بسط Laurent شکل (26.1) دارد. سری (26.1) یک سری قدرت و. بنابراین، نه تنها در سوراخ شده، بلکه در کل محله همگرا می شود z-zq از جمله نقطه zo;مقدار آن S(z)تحلیلی است برای z و S(z) = )(ز)در 0 z - zoآر.بنابراین، یک حد محدود وجود دارد )(ز)\u003d Pm 5 (r) \u003d 5 (r) - بنابراین نقطه مفرد zq

ز->زو ز-*زو

قابل عرضه. قضیه ثابت شده است.

اظهار نظر. از اثبات قضیه برمی آید که در یک محل سوراخ شده 0 z - zo یک نقطه منفرد متحرک، تابع f(z)منطبق با تابع S(r) است که در کل محله تحلیلی است z - zo . بنابراین، اگر /(th) = را قرار دهیم S(zq)، سپس، بدون تغییر مقادیر تابع f(z)در هر نقطه از محله سوراخ شده، این تابع را در r تجزیه و تحلیل می کنیم، یعنی. "حذف" ویژگی. این اصطلاح "تکینگی قابل جابجایی" را توضیح می دهد. طبیعی است که چنین نقاطی را به صورت منظم در نظر بگیریم، نه به عنوان نقاط منفرد تابع f(z).

برای مثال تابع را در نظر بگیرید

در مثال 26.1 نشان داده شد که Pm (n) = 1. i.e. نقطه مفرد

zq = 0 قابل جابجایی است. با تنظیم /i(0) = 1، به این ترتیب تکینگی را حذف می کنیم و تابعی را به دست می آوریم که در نقطه تحلیلی است. zq = 0 (و در کل صفحه C).

اکنون اجازه دهید قطب ها را از نظر بسط های لوران مشخص کنیم.

قضیه 26.3. یک نقطه منفرد Zo تابع f(z) یک قطب اگر و فقط اگر است, زمانی که بخش اصلی بسط لوران با مرکز Zq فقط تعداد محدودی متمایز دارد.

از ضرایب صفر با n:

اثبات 1. اجازه دهید zq - قطب، یعنی. لیم /( z) = اوو.

اجازه دهید ثابت کنیم که بسط Laurent تابع f(z)دارای فرم (2G.2) می باشد. از آنجایی که لیم f(z)= اوو سپس یک محله سوراخ شده از نقطه وجود دارد

کی zq که در آن f(z)تحلیلی است و صفر ندارد. سپس تابع g(z) = 1 /f(z)در این محله سوراخ شده نیز تحلیلی خواهد بود و لیم g(z)= 0. بنابراین، Zoیکبار مصرف است *-؟ *0

نقطه منفرد تابع g(z).بیایید دوباره تعریف کنیم g(z)در نقطه zo، قرار دادن g(zo)= 0. سپس g(z)در کل همسایگی نقطه (پنچر نشده) تحلیلی می شود z 0 ,و z0صفر جدا شده آن خواهد بود. با نشان دادن نتعدد (ترتیب) این صفر. همانطور که در §23 نشان داده شد، در محله ای از نقطه تابع zq g(z)قابل نمایش به شکل (نگاه کنید به (23.2))

و (z$) f 0 و y>(z)در برخی از همسایگی های نقطه تحلیلی است زو-زیرا IP(z)پیوسته در نقطه zoو g>(zo) F 0" سپس IP(z)در برخی از محله های این نقطه نیز صفر ندارد. بنابراین تابع 1 /-p(z)همچنین در این محله تحلیلی خواهد بود و بنابراین در یک سری تیلور در آن گسترش می یابد:

با باز کردن پرانتزها و تغییر نام ضرایب، آخرین بسط را در فرم می نویسیم.

جایی که c_jv = 1>o f 0. بنابراین، بخش اصلی بسط لورنت f(r) فقط شامل تعداد متناهی عبارت است. ما به برابری لازم (26.2) رسیده ایم.

2. اجازه دهید در یک محله سوراخ شده از یک نقطه هفتمعملکرد )(ز)با بسط Laurent (26.2) نشان داده می شود (به شکل گسترده تر، به (26.3) مراجعه کنید)، که بخش اصلی آن فقط شامل تعداد محدودی از عبارت است، و با-د" f 0. ما باید این را ثابت کنیم Zq - قطب تابع f(z).ضرب برابری (26.3) در (G - جی o) iV، تابع را دریافت می کنیم

سری در (26.4) یک سری توانی است که به یک تابع تحلیلی همگرا می شود نه تنها در نقطه سوراخ شده، بلکه در کل همسایگی نقطه Zq. بنابراین، تابع h(z)در این همسایگی تحلیلی می شود اگر با تنظیم آن را در هفتم گسترش دهیم h(zo)= s_dg f 0. سپس

بنابراین نقطه o یک قطب است و قضیه 26.3 ثابت می شود.

تعدد (ترتیب) تابع صفر g(z)= 1//(r) نامیده می شود سفارش قطبتابع /(r). اگر یک N-پس ترتیب قطب هفتم است g(z)= (r - Zo)N ip(z)،و برو) اف 0، و همانطور که در قسمت اول اثبات قضیه 26.3 نشان داده شده است، بسط f(r) به شکل (26.3) است، که در آن c_/v f 0. برعکس، اگر f(r) به سری (26.3) و e-z F 0، سپس

t.s. N-ترتیب قطب تابع f(r). به این ترتیب، ترتیب قطب zq تابع/(G) برابر است با تعداد ضریب غیرصفر اصلی بخش اصلی انبساط لوران در همسایگی سوراخ شده نقطه zq(یعنی برابر با چنین عددی است N،چه s_dg f 0 و sp= 0 در پ > ن).

اجازه دهید ادعای زیر را که راحت است) برای برنامه ها اثبات کنیم.

نتیجه 26.4. نقطه zq قطبی از مرتبه N داستان است/(G) اگر و تنها اگر/(G) در فرم نشان دهند

که در آن h(z) یک تابع تحلیلی در همسایگی یک نقطه استهفتم و h(zo) f 0.

اثبات عملکرد cp(z) = l/h(z)در برخی از همسایگی های نقطه r تحلیلی است. شرط نتیجه 26.4 معادل زیر است:

از همین رو zq - تعدد صفر نکارکرد g(z).و از این رو قطب کثرت نتوابع /(2).

مثال دوم 26.5. نقاط منفرد جدا شده یک تابع را پیدا کنید و نوع آنها را مشخص کنید.

D e u c tio n نقاطی که در آن (z 2 + 1 )(z+ H) 2 = 0. اگر z 2 L- 1 = 0 سپس 2 = ± rاگر (z 4- H) 2 = 0، سپس z= -3. بنابراین تابع دارای سه نقطه مفرد است z= r، 22 = -r، ز3 = - 3. در نظر بگیرید z:

G -قطب مرتبه اول (ما از نتیجه 26.4 استفاده کردیم). می توان به طور مشابه ثابت کرد که 22 = -منهمچنین یک قطب از درجه اول. برای 2 ساعت داریم:

اجازه دهید به بررسی نکات اساساً مفرد بپردازیم.

قضیه 26.6. یک نقطه منفرد zq از تابع f(z) اساساً منفرد است اگر و فقط در صورتی که بخش اصلی بسط لورنت با مرکز zq بی نهایت متفاوت باشد. صفر، ضرایب با p.

اثبات قضیه 26.6 مستقیماً از قضایای 26.2 و 26.3 پیروی می کند. در واقع، اگر نقطه zq اساساً مفرد است، پس بخش اصلی بسط Laurent نمی تواند وجود نداشته باشد یا شامل تعداد محدودی از عبارت باشد (در غیر این صورت نقطه Zq یا قابل جابجایی خواهد بود یا یک قطب). بنابراین تعداد اصطلاحات قسمت اصلی باید بی نهایت باشد.

برعکس، اگر قسمت اصلی شامل بی نهایت اعضا باشد، پس Zq نه می تواند یک نقطه قابل جابجایی باشد و نه یک قطب. در نتیجه، این نقطه اساساً مفرد است.

طبق تعریف، یک نقطه اساساً منفرد با این واقعیت مشخص می شود که تابع f(2) نه محدود و نه حد نامتناهی برای آن دارد. z ->zq یک ایده کامل تر از اینکه چقدر رفتار یک تابع در همسایگی یک نقطه اساساً منفرد نامنظم است با قضیه زیر ارائه می شود.

قضیه 26.7 (قضیه سوچوکی). اگر zq اساساً مفرد است، نقطه تابع f(z), سپس برای هر عدد مختلط L، از جمله A =اوه، دنباله ای از نقاط z n وجود دارد که z n -> zo ولیم f(zn) = ولی.

n->os

اثبات ابتدا مورد را در نظر بگیرید A =اوه در قسمت اول اثبات قضیه 2G.2، مشخص کردیم که اگر f(z)در یک محله سوراخ شده از نقطه r0 محدود شده است، سپس تمام ضرایب c، n = - 1, - 2,... از قسمت اصلی برابر با صفر هستند (و در نتیجه تکینگی در th قابل جابجایی است). از آنجایی که با فرض r0 یک نقطه اساساً منفرد است، تابع f(r) در هر همسایگی سوراخ شده نقطه r0 نامحدود است. اجازه دهید مقداری همسایه باریک 0 Z را طوری در نظر بگیریم که f(zi) > 1 (اگر |/(r)| z - zo R/2 یک نقطه وجود دارد z-2 ، جایی که |/(dd)| > 2 و غیره: در محله سوراخ شده O 71. بدیهی است که rn -e go و lim /(r«) = oo. بنابراین، در مورد A = oo، قضیه 26.7

ثابت شده است.

بگذار حالا A fاوه ابتدا فرض کنید یک محله سوراخ شده 0 وجود دارد

= -yy---- در این محله سوراخ شده تحلیلی خواهد بود و در نتیجه،

/(G) - ولی

در نتیجه، r یک نقطه منفرد جدا شده از تابع Φ(r) است. بیایید نشان دهیم. که r0 اساساً یک نقطه منفرد از Φ(r) است. بذار اشتباه باشه سپس یک حد محدود Φ(r)، یا متناهی یا نامتناهی وجود دارد. زیرا

/(r) = A +، سپس Hsh /(r) نیز وجود دارد که با شرط تناقض دارد

F(g) ~ :-*z 0

دیدگاه قضیه بنابراین r0 یک نقطه اساساً منفرد تابع Φ(r) است. طبق آنچه در بالا ثابت شد، دنباله ای از نقاط r n وجود دارد که r n o و lim Φ(r n) = oo. از اینجا

ما ادعای لازم را با این فرض ثابت کردیم که f(r) F Aدر برخی از محله های سوراخ شده نقطه r. اجازه دهید فرض کنیم که این درست نیست، i.e. در هر محله کوچک سوراخ شده خودسرانه نقطه ام چنین نقطه ای وجود دارد G",که f(r") = A. سپس برای هر پدر محله سوراخ شده 0 f(z u) = L. بنابراین، ادعای مورد نیاز درست است پ-یوو

در همه موارد، و قضیه 26.7 ثابت شده است.

با توجه به قضیه 26.7 (سوخوتسکی)، در هر محله سوراخ شده (به طور خودسرانه کوچک) از یک نقطه اساساً منفرد، تابع f(r) مقادیری به طور دلخواه نزدیک به هر عددی در صفحه مختلط توسعه یافته C می گیرد.

برای مطالعه نقاط منفرد جدا شده، بسط های معروف تیلور از توابع ابتدایی اولیه اغلب مفید هستند.

مثال 2G.8. نوع نقطه مفرد zq = 0 را برای تابع تعیین کنید

حل شد و e. صورت و مخرج را در یک سری تیلور در توان های r بسط می دهیم. جایگزین کردن به (22.11) 3 zبه جای r و تفریق 1، به دست می آوریم

با استفاده از (22.12)، بسط مخرج را بدست می آوریم:

سری در این بسط ها در کل صفحه پیچیده € همگرا می شوند. ما داریم

و /2(2) در همسایگی نقطه مشابه هستند زو = 0 (و حتی در کل صفحه) و /2 (20) اف 0، سپس h(z)همچنین در برخی از همسایگی های نقطه gF 0 تحلیلی است. طبق نتیجه 26.4، نقطه زو = 0 قطب سفارش است N = 4.

مثال دوم 26.9. نقاط مفرد یک تابع را پیدا کنید f(z)= sin j - و نوع آنها را مشخص کنید.

P e در e و e. تابع دارای یک نقطه منفرد نهایی است zq = 1. در نقاط دیگر از C، تابع w =--- تحلیلی؛ از این رو تابع گناه wتحلیلی خواهد بود.

جایگزینی در انبساط سینوس (22.12) - به جای r، می گیریم

ما بسط تابع sin را در یک سری Laurent در یک همسایگی سوراخ شده از نقطه 20 = 1 به دست آورده ایم. از آنجایی که بسط حاصل شامل بی نهایت تعداد عبارت با توان منفی (r - 1) است، پس zq = 1 یک نقطه مفرد ضروری است (در این مورد، بسط Laurent فقط از قسمت اصلی تشکیل شده است و قسمت صحیح وجود ندارد).

توجه داشته باشید که در این مورد نیز می‌توان ماهیت تکینگی را مستقیماً از تعریف، بدون توسل به بسط سری مشخص کرد. در واقع، دنباله های (r") و (2") همگرا هستند zo= 1، و به این ترتیب که f(z" n)= 1، /(2") = 0 (این توالی ها را خودتان مشخص کنید). f(z)زمانی که محدودیتی ندارد z -> 1 و از این رو نکته zq - 1 اساساً مفرد است.

اجازه دهید مفهوم بسط لورن یک تابع در همسایگی یک نقطه را معرفی کنیم Zq = 00 و ارتباط بین بسط و ماهیت تکینگی را در این نقطه در نظر بگیرید. توجه داشته باشید که تعاریف یک نقطه منفرد جدا شده و نوع آن (قابل جابجایی، قطبی یا اساساً منفرد) به این مورد منتقل می شود. zq = oc بدون تغییر. اما قضایای 26.2. 26.3 و 26.6، مربوط به ماهیت بسط های Laurent، نیاز به تغییر دارند. نکته این است که اعضا c n (z - 2o) ص. پ= -1،-2،...، بخش اصلی، تعریف "بی نظمی" تابع نزدیک به نقطه پایانی Zq، از آنجایی که 2 به oo تمایل دارد، آنها "درست" رفتار خواهند کرد (تمایل به 0). برعکس، اعضای قسمت منظم با پ= 1،2،... به oo تمایل دارد. آنها ماهیت تکینگی را در تعیین می کنند Zq = اوو. بنابراین، بخش اصلی گسترش در همسایگی oo، شرایط دارای قدرت های مثبت خواهد بود پ،و صحیح - با منفی.

بیایید یک متغیر جدید معرفی کنیم w = 12. عملکرد tv= 1/2، بسط داده شده به طوری که u(oo) = 0، یک به یک و به طور منسجم همسایگی را ترسیم می کند z > Rنکته ها zq = 00 در همسایگی |w| wq = 0. اگر تابع f(z)تجزیه و تحلیل در یک محله سوراخ شده آر z Zq = oc، سپس تابع G(w) = f(l/w)در همسایگی زرد 0 wo = 0 تحلیلی خواهد بود. زیرا برای 2 -> oo وجود خواهد داشت w-> 0، سپس

از همین رو G(w)در نقطه دارد wq = 0 تکینگی از همان نوع است f(z)در نقطه Zq = 00. اجازه دهید تابع G(w) را در یک سری Laurent در یک محله سوراخ شده از نقطه wo = 0 گسترش دهیم:

مجموع سمت راست (26.5) به ترتیب نشان دهنده قسمت های صحیح و اصلی بسط است. بیایید به سراغ متغیر برویم z،جایگزین کردن w = 1/z:

دلالت می کند پ\u003d -A *، 6 * \u003d 6_ " \u003d با صو توجه به آن G(l/z) = f(z)، ما گرفتیم

تجزیه (2G.G) نامیده می شود بسط لوران تابع f(z) در همسایگی سوراخ شده نقطه zq= اوو اولین مجموع در (2G.6) نامیده می شود قسمت راست، و جمع دوم است بخش اصلیاین تجزیه از آنجایی که این مجموع با قسمت های صحیح و اصلی بسط مطابقت دارد (26.5)، بسط (26.6) مشابه قضایای 26.2، 26.3، و 26.6 را برآورده می کند. بنابراین، قضیه زیر مشابه قضیه 26.2 است.

قضیه 26.10. نقطه منفرد جدا شدهZq - سیستم عامل (کارکرد/(G) قابل جابجایی است اگر و تنها در صورتی که بسط لورن در محله سوراخ شده این نقطه شکل داشته باشد

t.s. فقط از قسمت صحیح تشکیل شده است.

ما /(oo) = قرار می دهیم شرکتتابع تعریف شده توسط سری (26.7) همگرا در همسایگی z > Rنقاط 2o \u003d oc، فراخوانی شد تحلیلی در نقطه z o = اوو. (توجه داشته باشید که این تعریف معادل تحلیلی بودن تابع است G(w) در نقطه وای = 0.)

مثال 26.11. نقطه مفرد zq = oo تابع را بررسی کنید

از آنجایی که حد محدود است، پس زو = oo یک نقطه منفرد قابل جابجایی تابع f(r) است. اگر /(oo) = lim قرار دهیم J(z)= 0، سپس f(z)خواهد شد

تیک در نقطه Zo= سیستم عامل اجازه دهید نشان دهیم که چگونه بسط مربوطه را پیدا کنیم (26.7). بیایید به سراغ متغیر برویم w = 1 fz.جایگزین کردن z= 1 /?e، دریافت می کنیم

(آخرین تساوی در همسایگی سوراخ شده نقطه ww = 0 معتبر است، اما ما تعریف (7(0) = 0 را گسترش می دهیم). تابع حاصل دارای نقاط منفرد است. w =± من، w =-1/3، و در نقطه Wq = 0 تحلیلی است. تابع گسترش G(w)بر حسب درجه w(همانطور که در مثال 25.7 انجام شد) و جایگزین کردن به سری توان حاصل w = 1/zمی توان بسط (26.7) تابع را بدست آورد f(z).

قضیه 26.3 برای مورد zo= oo به شکل زیر بازنویسی می شود.

قضیه 26.12. نقطه منفرد جدا شدهبرو = oc تابع f(z) یک قطب است اگر و فقط اگر بخش اصلی بسط لوران باشد (26.6) فقط تعداد محدودی از ضرایب غیر صفر داردبا":

در اینجا سری قسمت منظم است و چند جمله ای پرانتز شده بخش اصلی بسط است. تعدد قطب در oc به عنوان تعدد قطب تعریف می شود wq = 0 توابع G(z).به راحتی می توان فهمید که تعدد قطب با عدد منطبق است ندر (26.8).

Q p | (i 2 + 1) (z + 3) 2

یک وظیفه. نشان می دهد که تابع f(z) =-- -- دارد در

نقطه زو =سفارش قطب oo 3.

قضیه 26.6 در مورد یک نقطه مفرد اساسی برای مورد بازنویسی شده است zo= os تقریباً کلمه به کلمه است، و ما در مورد آن به تفصیل نمی پردازیم.

مفاهیم و تعاریف اساسی:

صفر تابع تحلیلی f(z) نقطه “a” است که برای آن f(a)=0 است.

صفر مرتبه "n" تابع f(z) نقطه "a" است اگر اما fn(a)10.

یک نقطه منفرد "a" یک نقطه منفرد از تابع f(z) نامیده می شود اگر همسایه ای از این نقطه وجود داشته باشد که در آن نقطه منفرد دیگری به جز "a" وجود نداشته باشد.

نقاط مفرد جدا شده بر سه نوع هستند: .

1 نقطه ویژه قابل جابجایی؛

3 نکته مفرد ضروری

نوع یک نقطه منفرد را می توان بر اساس رفتار یک تابع معین در نقطه منفرد یافت شده و همچنین از شکل سری لوران به دست آمده برای تابع در همسایگی نقطه مفرد یافت شده تعیین کرد.

تعیین نوع یک نقطه منفرد با رفتار تابع در آن.

1. نقاط منفرد قابل جابجایی.

یک نقطه منفرد جدا شده a از تابع f(z) در صورت وجود یک حد محدود قابل جابجایی نامیده می شود.

2. قطب.

یک نقطه مفرد جدا شده a از تابع f(z) را قطب if می نامند .

3. نقاط مفرد مهم.

یک نقطه مفرد جدا شده a تابع f(z) در صورتی که نه متناهی و نه نامتناهی وجود داشته باشد، نقطه مفرد ضروری نامیده می شود.

رابطه زیر بین صفر و قطب تابع برقرار است.

برای اینکه یک نقطه a قطبی از مرتبه n تابع f(Z) باشد، لازم و کافی است که این نقطه برای تابع صفر از مرتبه n باشد.

اگر n=1 قطب ساده نامیده می شود.

تعریف:یک نقطه منفرد جدا شده از یک کاراکتر تک ارزشی نامیده می شود:

الف) در صورتی که قسمت اصلی تجزیه وجود نداشته باشد قابل جابجایی است.

ب) یک قطب اگر قسمت اصلی شامل تعداد محدودی از اعضا باشد.

ج) یک نقطه اساساً مفرد اگر قسمت اصلی شامل تعداد نامتناهی جمله باشد.

الف) بنابراین، در همسایگی یک نقطه منفرد قابل جابجایی، بسط به شکل زیر است:

این تابع را در تمام نقاط دایره بیان می کند |z-a|

در مرکز z=a، برابری نادرست است، زیرا تابع z=a دارای ناپیوستگی است و سمت راست پیوسته است. اگر مقدار تابع در مرکز تغییر کند، آن را برابر با مقدار سمت راست در نظر بگیرید، شکاف حذف خواهد شد - از این رو نام آن - قابل جابجایی است.

ب) در همسایگی قطبی از مرتبه m، بسط سری Laurent به شکل زیر است:

ج) در همسایگی یک قطب ساده

کسر و فرمول برای محاسبه آنها.

باقیمانده یک تابع تحلیلی f(z) در یک نقطه منفرد جدا شده z 0 عدد مختلطی برابر با مقدار انتگرال است. ، در جهت مثبت در امتداد دایره L به مرکز نقطه z 0 ، که در ناحیه تحلیلی تابع f(z) قرار دارد (یعنی در حلقه 0) گرفته شده است.<|z-z0|

باقیمانده تابع f(z) در یک نقطه منفرد جدا شده z 0 با نماد Res f(z 0) یا Res (f(z)؛ z 0 نشان داده می شود. به این ترتیب،

Resf(z0)= . (22.15.1)

اگر n=-1 را در فرمول (22.15.1) قرار دهیم، دریافت می کنیم:

C-1=

یا Res f(z 0)= C -1،

آن ها باقیمانده تابع f(z) نسبت به نقطه مفرد z 0 برابر با ضریب جمله اول با توان منفی در بسط تابع f(z) در سری لوران است.

محاسبه کسورات.

نقاط منفرد منظم یا قابل جابجایی. بدیهی است که اگر z=z 0 یک نقطه منفرد منتظم یا قابل جابجایی تابع f(z) باشد، Res f(z 0)=0 (در این موارد هیچ بخش اصلی در تجزیه لوران وجود ندارد، بنابراین c-1= 0).

قطب. نقطه z 0 یک قطب ساده از تابع f(z) باشد. سپس سری Laurent برای تابع f(z) در همسایگی نقطه z 0 به شکل زیر است:

از اینجا

بنابراین، با عبور از این برابری به حد z --z 0، به دست می آوریم

Res f(z0)=

اساسا نکته خاصی اگر نقطه z 0 اساساً نقطه مفرد تابع f(z) باشد، برای محاسبه باقیمانده تابع در این نقطه، معمولاً مستقیماً ضریب c-1 در بسط تابع در یک سری لوران تعیین می شود.

طبقه بندی رویداد مجموع، حاصلضرب رویدادها، خواص آنها، نمایش گرافیکی.

رویدادها به دو دسته تقسیم می شوند:

1. تصادفی

2. معتبر

3. غیر ممکن

قابل اعتماد - این رویدادی است که لزوماً در این شرایط رخ می دهد (شب به دنبال صبح است).

تصادفی رویدادی است که ممکن است رخ دهد یا نباشد (گذراندن امتحان).

غیرممکن رویدادی است که در شرایط داده شده رخ نخواهد داد (یک مداد سبز را فقط با مدادهای قرمز از جعبه خارج کنید).