Konsep trapesium melengkung. Topik: Trapesium lengkung dan luasnya. Pembentukan konsep dan metode tindakan baru

Suatu bangun datar yang dibatasi oleh grafik fungsi non-negatif kontinu $f(x)$ pada ruas $$ dan garis $y=0, \ x=a$ dan $x=b$ disebut trapesium lengkung.

Luas trapesium lengkung yang bersesuaian dihitung dengan rumus:

$S=\int\batas_(a)^(b)(f(x)dx).$ (*)

Kami akan membagi soal secara kondisional untuk mencari luas trapesium lengkung menjadi tipe $4$. Mari kita lihat masing-masing jenis lebih detail.

Tipe I: trapesium melengkung ditentukan secara eksplisit. Kemudian segera terapkan rumus (*).

Misalnya, cari luas trapesium lengkung yang dibatasi oleh grafik fungsi $y=4-(x-2)^(2)$ dan garis $y=0, \ x=1$ dan $x =3$.

Mari menggambar trapesium melengkung ini.

Dengan menggunakan rumus (*), kita mencari luas trapesium lengkung ini.

$S=\int\limits_(1)^(3)(\left(4-(x-2)^(2)\right)dx)=\int\limits_(1)^(3)(4dx)- \int\limits_(1)^(3)((x-2)^(2)dx)=4x|_(1)^(3) – \kiri.\frac((x-2)^(3) )(3)\kanan|_(1)^(3)=$

$=4(3-1)-\frac(1)(3)\kiri((3-2)^(3)-(1-2)^(3)\kanan)=4 \cdot 2 – \frac (1)(3)\kiri((1)^(3)-(-1)^(3)\kanan) = 8 – \frac(1)(3)(1+1) =$

$=8-\frac(2)(3)=7\frac(1)(3)$ (satuan$^(2)$).

Tipe II: trapesium lengkung ditentukan secara implisit. Dalam hal ini, garis lurus $x=a, \ x=b$ biasanya tidak ditentukan atau ditentukan sebagian. Dalam hal ini, Anda perlu mencari titik potong fungsi $y=f(x)$ dan $y=0$. Poin ini akan menjadi poin $a$ dan $b$.

Misalnya, mencari luas bangun yang dibatasi oleh grafik fungsi $y=1-x^(2)$ dan $y=0$.

Mari kita cari titik potongnya. Untuk melakukan ini, kita menyamakan ruas kanan dari fungsi-fungsi tersebut.

Jadi, $a=-1$ dan $b=1$. Mari menggambar trapesium melengkung ini.

Mari kita cari luas trapesium lengkung ini.

$S=\int\limits_(-1)^(1)(\left(1-x^(2)\right)dx)=\int\limits_(-1)^(1)(1dx)-\int \limits_(-1)^(1)(x^(2)dx)=x|_(-1)^(1) – \kiri.\frac(x^(3))(3)\kanan|_ (-1)^(1)=$

$=(1-(-1))-\frac(1)(3)\kiri(1^(3)-(-1)^(3)\kanan)=2 – \frac(1)(3) \kiri(1+1\kanan) = 2 – \frac(2)(3) = 1\frac(1)(3)$ (satuan$^(2)$).

Tipe III: luas bangun yang dibatasi oleh perpotongan dua fungsi tak negatif kontinu. Angka ini bukan trapesium lengkung, artinya luasnya tidak dapat dihitung menggunakan rumus (*). Bagaimana menjadi? Ternyata luas gambar tersebut dapat dicari selisih antara luas trapesium lengkung yang dibatasi oleh fungsi atas dan $y=0$ ($S_(uf)$), dan fungsi bawah dan $y =0$ ($S_(lf)$), di mana peran $x=a, \ x=b$ dimainkan oleh koordinat $x$ dari titik potong fungsi-fungsi ini, yaitu.

$S=S_(uf)-S_(lf)$. (**)

Hal terpenting saat menghitung luas seperti itu adalah jangan “kelewatan” dalam memilih fungsi atas dan bawah.

Misalnya, mencari luas bangun yang dibatasi oleh fungsi $y=x^(2)$ dan $y=x+6$.

Mari kita cari titik potong grafik berikut:

Menurut teorema Vieta,

$x_(1)=-2,\x_(2)=3.$

Artinya, $a=-2,\b=3$. Mari kita menggambar sebuah gambar:

Jadi, fungsi teratas adalah $y=x+6$, dan fungsi bawah adalah $y=x^(2)$. Selanjutnya kita mencari $S_(uf)$ dan $S_(lf)$ menggunakan rumus (*).

$S_(uf)=\int\limits_(-2)^(3)((x+6)dx)=\int\limits_(-2)^(3)(xdx)+\int\limits_(-2 )^(3)(6dx)=\kiri.\frac(x^(2))(2)\kanan|_(-2)^(3) + 6x|_(-2)^(3)= 32 0,5$ (satuan$^(2)$).

$S_(lf)=\int\limits_(-2)^(3)(x^(2)dx)=\left.\frac(x^(3))(3)\right|_(-2) ^(3) = \frac(35)(3)$ (satuan$^(2)$).

Mari kita substitusikan apa yang kita temukan ke dalam (**) dan dapatkan:

$S=32,5-\frac(35)(3)= \frac(125)(6)$ (satuan$^(2)$).

Tipe IV: luas suatu bangun yang dibatasi oleh suatu fungsi yang tidak memenuhi syarat non-negatif. Untuk mencari luas bangun seperti itu, Anda harus simetris terhadap sumbu $Ox$ ( dengan kata lain, letakkan “minus” di depan fungsi) tampilkan area dan, dengan menggunakan metode yang diuraikan dalam tipe I – III, temukan luas area yang ditampilkan. Area ini akan menjadi area yang dibutuhkan. Pertama, Anda mungkin harus mencari titik potong grafik fungsi.

Misalnya, mencari luas bangun yang dibatasi oleh grafik fungsi $y=x^(2)-1$ dan $y=0$.

Mari kita cari titik potong grafik fungsi:

itu. $a=-1$, dan $b=1$. Mari kita menggambar luasnya.

Mari kita tampilkan luasnya secara simetris:

$y=0 \ \Panah Kanan \ y=-0=0$

$y=x^(2)-1 \ \Panah Kanan \ y= -(x^(2)-1) = 1-x^(2)$.

Hasilnya adalah trapesium lengkung yang dibatasi oleh grafik fungsi $y=1-x^(2)$ dan $y=0$. Ini adalah masalah untuk menemukan trapesium lengkung tipe kedua. Kami sudah menyelesaikannya. Jawabannya adalah: $S= 1\frac(1)(3)$ (satuan $^(2)$). Artinya luas trapesium lengkung yang diperlukan adalah:

$S=1\frac(1)(3)$ (satuan$^(2)$).

Luas trapesium melengkung

Trapesium lengkung adalah bangun datar yang dibatasi oleh grafik yang diberikan pada ruas [ A, B] fungsi kontinu dan non-negatif F(X), ordinat yang ditarik pada titik-titik A Dan B, dan segmen sumbu Sapi antar titik A Dan B(Lihat Gambar 2).

Mari kita buktikan pernyataan berikut.

Trapesium lengkung adalah bangun persegi, luas P

Bukti. Sejak kontinu pada ruas [ A, B] fungsinya dapat diintegralkan, maka untuk bilangan positif apa pun ε Anda dapat menentukan partisi seperti itu T segmen [ A, B], Apa bedanya S - S < ε , Di mana S Dan S- masing-masing jumlah partisi atas dan bawah T. Tetapi S Dan S masing-masing sama S D Dan S Saya, Di mana S D Dan S Saya- luas bangun berundak (poligon), yang pertama berisi trapesium lengkung, dan yang kedua berisi trapesium lengkung (Gbr. 2 juga menunjukkan bangun berundak ini). Karena S D - S Saya < ε , maka berdasarkan Teorema 1, trapesium lengkung adalah persegi. Karena limit Δ → 0 jumlah atas dan bawah sama dengan S ≤ P ≤ S, lalu luasnya P trapesium lengkung dapat dicari dengan menggunakan rumus (1).

Komentar. Jika fungsinya F(X) kontinu dan non-positif pada segmen [ A, B], maka nilai integralnya sama dengan luas trapesium lengkung yang diambil tanda negatifnya, dibatasi oleh grafik fungsi F(X), ordinat di titik-titik A Dan B dan segmen sumbu Sapi antar titik A Dan B. Oleh karena itu, jika F(X) berubah tanda, maka sama dengan jumlah luas trapesium lengkung yang terletak di atas dan di bawah sumbu, diambil dengan tanda tertentu Sapi, dan luas daerah pertama diambil dengan tanda +, dan luas daerah kedua diambil dengan tanda -.

Luas sektor melengkung

Biarkan kurva L diberikan dalam sistem koordinat kutub dengan persamaan R = R(θ ), α ≤ θ ≤ β (lihat Gambar 3), dan fungsinya R(θ ) kontinu dan non-negatif pada segmen [ α , β ]. Suatu bangun datar yang dibatasi oleh suatu kurva L dan dua sinar membentuk sudut dengan sumbu kutub α Dan β , kami akan menelepon sektor lengkung.

Mari kita buktikan pernyataan berikut. Sektor lengkung adalah bangun persegi, luas P yang dapat dihitung dengan menggunakan rumus

Bukti. Pertimbangkan partisinya T segmen [ α , β ] titik α = θ 0 < θ 1 < ... < θ N = β dan untuk setiap segmen parsial [ θ Saya -1 , θ Saya] buatlah sektor melingkar yang jari-jarinya sama dengan minimum R Saya dan maksimal R Saya nilai-nilai R(θ ) pada segmen [ θ Saya -1 , θ Saya]. Hasilnya, kita memperoleh dua gambar berbentuk kipas, yang pertama terdapat pada sektor lengkung, dan yang kedua berisi sektor lengkung (gambar berbentuk kipas ini ditunjukkan pada Gambar 3). Luas bangun berbentuk kipas yang ditunjukkan masing-masing sama dengan dan. Perhatikan bahwa jumlah pertama adalah jumlah yang lebih rendah S untuk fungsi untuk partisi tertentu T segmen [ α , β ], dan jumlah kedua adalah jumlah teratas S untuk fungsi yang sama dan partisi yang sama. Karena fungsinya dapat diintegrasikan pada segmen [ α , β ], maka selisihnya bisa sekecil yang diinginkan. Misalnya untuk apapun yang tetap ε > 0 selisih ini dapat diperkecil ε /2. Sekarang mari kita tuliskan sebuah poligon ke dalam gambar berbentuk kipas bagian dalam Q Saya dengan luas S Saya, yang mana , dan kami mendeskripsikan poligon di sekitar gambar luar berbentuk kipas Q D daerah S D, untuk itu * . Jelasnya, poligon pertama tertulis di sektor lengkung, dan poligon kedua dibatasi di sekitarnya. Karena ketidaksetaraan itu benar

Definisi. Selisih F (b) – F (a) disebut integral fungsi f (x) pada interval [ a ; b ] dan dilambangkan sebagai berikut: = F (b) – F (a) – rumus Newton-Leibniz.

Arti geometris dari integral.

Luas trapesium lengkung yang dibatasi oleh grafik positif kontinu pada interval [a; b ] fungsi f (x), sumbu Sapi dan garis x=a dan x= b:

Menghitung luas menggunakan integral.

1.Luas suatu bangun yang dibatasi oleh grafik negatif kontinu pada interval [a; b ] fungsi f (x), sumbu Sapi dan garis x=a dan x= b:

2. Luas bangun yang dibatasi oleh grafik fungsi kontinu f (x) dan garis x=a, x= b:

3. Luas bangun yang dibatasi oleh grafik fungsi kontinu f(x) dan:

4. Luas bangun yang dibatasi oleh grafik fungsi kontinu f(x) dan sumbu Ox:

Soal dan tes pada topik "Integral. Perhitungan luas menggunakan integral"

• Integral

  Pelajaran: 4 Tugas: 13 Tes: 1

• Menghitung luas menggunakan integral - Antiturunan dan integral kelas 11

  Pelajaran: 1 Tugas: 10 Tes: 1

• Antiturunan - Antiturunan dan integral kelas 11

  Pelajaran: 1 Tugas: 11 Tes: 1

• Planimetri: perhitungan panjang dan luas

  Tugas: 7

• Perhitungan dan Konversi - Persiapan Ujian Negara Terpadu Matematika

  Tugas: 10

Sebelum Anda mulai menghitung luas suatu bangun yang dibatasi oleh garis-garis tertentu, cobalah menggambarkan bangun tersebut dalam sistem koordinat. Ini akan membuat penyelesaian masalah menjadi lebih mudah.

Mempelajari materi teori tentang topik ini memberi Anda kesempatan untuk menguasai konsep antiturunan dan integral, memahami hubungan antar keduanya, menguasai teknik kalkulus integral yang paling sederhana, dan belajar menerapkan integral dalam menghitung luas bangun datar yang dibatasi oleh grafik fungsi. .

Contoh.

1. Hitung integralnya

Larutan:

Menjawab: 0.

2. Carilah luas bangun yang dibatasi oleh garis

A) F(X) = 2 X – X 2 dan sumbu x

Larutan: Grafik fungsi f(x) = 2x - x 2 adalah parabola. Puncak: (1; 1).

Menjawab:(satuan persegi).

Tidak ada tanggal________

Subjek:Trapesium lengkung dan luasnya B

Tujuan Pelajaran: Pengertian trapesium lengkung dan luasnya, belajar menghitung luas trapesium lengkung.

SELAMA KELAS

1. Momen organisasi.

Menyapa siswa, memeriksa kesiapan kelas menghadapi pelajaran, mengatur perhatian siswa, mengungkapkan tujuan umum pelajaran dan rencananya.

2. Tahap pengecekan pekerjaan rumah.

Tujuan: Untuk menetapkan kebenaran, kelengkapan dan kesadaran pelaksanaan pekerjaan rumah oleh semua siswa, untuk mengidentifikasi kesenjangan dalam pengetahuan siswa dan metode kegiatan. Tentukan penyebab kesulitan dan hilangkan kesenjangan yang ditemukan.

3. Tahap pembaruan.

Tujuan: menjamin motivasi belajar anak sekolah, diikutsertakan dalam kegiatan bersama untuk menentukan tujuan pembelajaran. Perbarui pengalaman subjektif siswa.

Mari kita ingat konsep dasar dan rumusnya.

Definisi. Fungsi kamu=F(x), x (a,b), disebut antiturunan dari fungsi tersebut kamu=f(x), x (a,b), jika untuk semua orang X (a,b) kesetaraan berlaku

F (x)=f(x).

Komentar. Jika F(X) ada antiturunan untuk fungsi tersebut f(x), lalu untuk konstanta apa pun DENGAN, F(x)+C juga merupakan antiturunan untuk f(x).

Masalah menemukan semua antiturunan suatu fungsi f(x) disebut integrasi, dan himpunan semua antiturunan disebut integral tak tentu untuk fungsi tersebut f(x) Oleh dx dan ditunjuk

Properti berikut terjadi:

1 . ;

2 . Jika C= Konstan, kalau begitu
;

3 .
.

Komentar. Dalam pelajaran matematika sekolah, istilah “integral tak tentu” tidak digunakan; sebaliknya, mereka mengatakan “himpunan semua antiturunan.”

Berikut adalah tabel integral tak tentu.

Contoh 1. Temukan antiturunan untuk suatu fungsi
, melewati titik tersebut M(2;4).

Larutan. Himpunan semua antiturunan suatu fungsi
ada integral tak tentu
. Mari kita hitung menggunakan sifat integral 1 dan 2. Kita punya:

Kami menemukan bahwa himpunan semua antiturunan diberikan oleh sekumpulan fungsi kamu=F(x)+C, itu adalah kamu=x 3 – 2x+C, Di mana DENGAN– konstanta sewenang-wenang.

Mengetahui bahwa antiturunan melewati suatu titik M(2;4), substitusikan koordinatnya ke ekspresi sebelumnya dan temukan DENGAN.

4=2 3 –2 2+DENGAN  DENGAN=4–8+4; DENGAN=0.

Menjawab: F(x)=x 3 - 2X- antiturunan yang diinginkan.

4. Pembentukan konsep dan metode tindakan baru.

Tujuan: Untuk memastikan bahwa siswa memahami, memahami dan mengingat materi yang dipelajari. Memastikan siswa menguasai metode mereproduksi materi yang dipelajari, meningkatkan pemahaman filosofis tentang konsep, hukum, aturan, dan rumus yang diperoleh. Menetapkan kebenaran dan kesadaran siswa terhadap materi yang dipelajari, mengidentifikasi kesenjangan pemahaman awal, dan melakukan koreksi. Pastikan siswa menghubungkan pengalaman subjektif mereka dengan tanda-tanda pengetahuan ilmiah.

Menemukan luas bangun datar

Masalah pencarian luas bangun datar erat kaitannya dengan masalah pencarian antiturunan (integrasi). Yaitu: luas trapesium lengkung yang dibatasi oleh grafik suatu fungsikamu=f(x) (f(x)> 0) lurusx=sebuah; x=b; kamu= 0, sama dengan selisih antara nilai antiturunan fungsi tersebutkamu=f(x) di poinB DanA :

S=F(b)–F(a)

Mari kita berikan definisi integral tertentu.

TENTANG
definisi. Biarkan fungsinya kamu=f(x) didefinisikan dan dapat diintegrasikan pada interval [ a,b] biarkan saja F(x)- beberapa prototipenya. Lalu nomornya F(b)–F(a) disebut integral dari A sebelum B fungsi f(x) dan ditunjuk

.

Persamaan
disebut rumus Newton-Leibniz.

Rumus ini menghubungkan masalah mencari luas bangun datar dengan integral.

Secara umum jika gambar tersebut dibatasi oleh grafik fungsi kamu=f(x);kamu=g(x) (f(x)>g(x)) dan lurus x=sebuah;x=b, maka luasnya sama dengan:

.

Contoh 2. Pada titik manakah pada grafik fungsi tersebut kamu=x 2 + 1 Anda perlu menggambar garis singgung sehingga terpotong dari gambar yang dibentuk oleh grafik fungsi ini dan garis lurus kamu= 0, x= 0, x= 1 trapesium yang luasnya paling besar?

Larutan. Membiarkan M 0 (X 0 ,y 0 ) – titik grafik fungsi kamu=x 2 + 1, di mana garis singgung yang diperlukan ditarik.

Mari kita cari persamaan tangennya kamu=kamu 0 +f (X 0 )(x–x 0 ) .

Kita punya:

Itu sebabnya

.

Temukan luas trapesium OABC.

.

B– titik potong garis singgung dengan garis lurus x= 1 

Tugasnya dikurangi menjadi menemukan nilai fungsi terbesar

S(X)=–x 2 +x+ 1 di segmen tersebut. Kami akan menemukannya S (X)=– 2x+ 1. Temukan titik kritis dari kondisi tersebut S (X)= 0  x=.

Kita melihat bahwa fungsi tersebut mencapai nilai terbesarnya pada x=. Kami akan menemukannya
.

Menjawab: garis singgungnya harus ditarik pada titik tersebut
.

Perhatikan bahwa masalah mencari integral berdasarkan makna geometrisnya sering dijumpai. Mari kita tunjukkan dengan sebuah contoh bagaimana masalah ini diselesaikan.

Contoh 4. Dengan menggunakan arti geometri integral, hitunglah

A )
; B)
.

Larutan.

A)
– sama dengan luas trapesium lengkung yang dibatasi oleh garis.

P mari kita bertransformasi

– bagian atas lingkaran dengan bagian tengahnya R(1;0) dan radius R= 1.

Itu sebabnya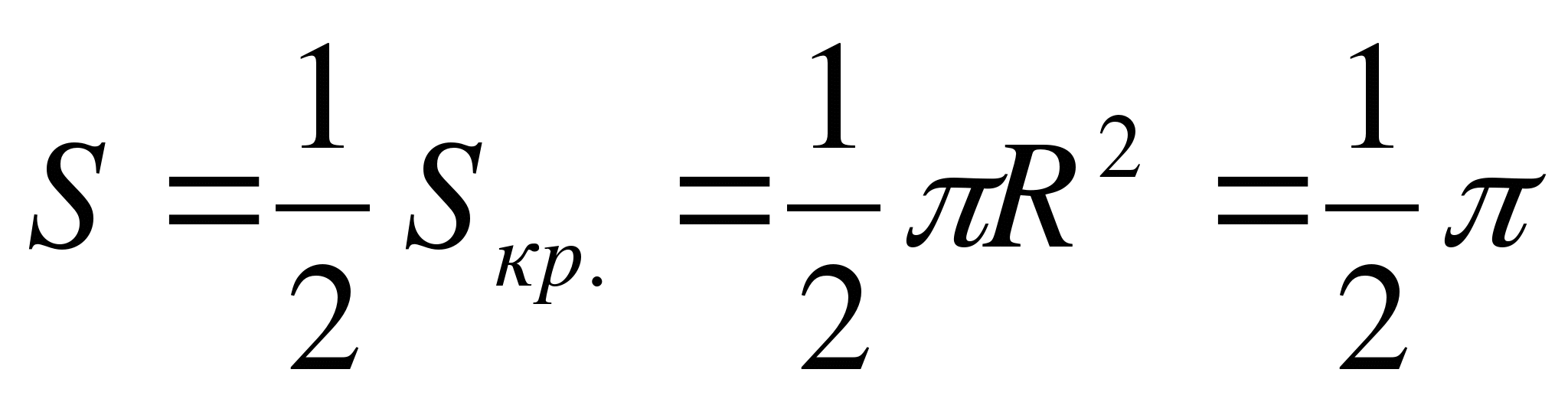
.

Menjawab:
.

b) Dengan argumen serupa, mari kita buatlah luas yang dibatasi oleh grafik .2 – 2x+ 2, bersinggungan dengannya di titik-titik A
, B(4;2)

kamu=–9X- 59, parabola kamu= 3X 2 +kapak+ 1, jika diketahui garis singgung parabola di titik tersebut x=– 2 dengan sumbu Sapi ukuran sudut arctg 6.

Menemukan A, jika diketahui luas trapesium lengkung yang dibatasi oleh garis kamu= 3X 3 + 2x, x=sebuah, kamu= 0 sama dengan satu.

Temukan luas terkecil suatu bangun datar yang dibatasi oleh parabola kamu=x 2 + 2X- 3 dan lurus kamu=kx+ 1.

6. Tahap informasi pekerjaan rumah.

Tujuan: Agar siswa memahami tujuan, isi dan cara menyelesaikan pekerjaan rumah No.18, 19,20,21 ganjil

7. Menyimpulkan pelajaran.

Tujuan: Untuk memberikan penilaian kualitatif terhadap hasil kerja kelas dan individu siswa.