مفهوم ذوزنقه منحنی. موضوع: ذوزنقه منحنی و مساحت آن. شکل گیری مفاهیم و روش های جدید عمل

شکلی که توسط نمودار یک تابع غیرمنفی $f(x)$ در قسمت $$ و خطوط $y=0، \ x=a$ و $x=b$ محدود شده باشد ذوزنقه منحنی نامیده می شود.

مساحت ذوزنقه منحنی متناظر با فرمول محاسبه می شود:

$S=\int\limits_(a)^(b)(f(x)dx).$ (*)

ما مسائل را به صورت مشروط برای یافتن مساحت ذوزنقه منحنی به انواع 4 دلاری تقسیم می کنیم. بیایید هر نوع را با جزئیات بیشتری بررسی کنیم.

نوع I: ذوزنقه خمیده به صراحت مشخص شده است.سپس بلافاصله فرمول (*) را اعمال کنید.

به عنوان مثال، مساحت یک ذوزنقه منحنی را پیدا کنید که با نمودار تابع $y=4-(x-2)^(2)$ و خطوط $y=0، \ x=1$ و $x محدود شده است. = 3 دلار

بیایید این ذوزنقه منحنی را ترسیم کنیم.

با استفاده از فرمول (*)، مساحت این ذوزنقه منحنی را پیدا می کنیم.

$S=\int\limits_(1)^(3)(\left(4-(x-2)^(2)\right)dx)=\int\limits_(1)^(3)(4dx)- \int\limits_(1)^(3)((x-2)^(2)dx)=4x|_(1)^(3) - \left.\frac((x-2)^(3) )(3)\right|_(1)^(3)=$

$=4(3-1)-\frac(1)(3)\left((3-2)^(3)-(1-2)^(3)\راست)=4 \cdot 2 - \frac (1)(3)\left((1)^(3)-(-1)^(3)\راست) = 8 – \frac(1)(3)(1+1) =$

$=8-\frac(2)(3)=7\frac(1)(3)$ (واحد$^(2)$).

نوع دوم: ذوزنقه منحنی به طور ضمنی مشخص شده است.در این مورد، خطوط مستقیم $x=a، \ x=b$ معمولاً مشخص نمی شوند یا تا حدی مشخص می شوند. در این حالت باید نقاط تقاطع توابع $y=f(x)$ و $y=0$ را پیدا کنید. این نقاط نقاط $a$ و $b$ خواهند بود.

برای مثال، مساحت یک شکل را که توسط نمودارهای توابع $y=1-x^(2)$ و $y=0$ محدود شده است، پیدا کنید.

بیایید نقاط تقاطع را پیدا کنیم. برای این کار، سمت راست توابع را برابر می کنیم.

بنابراین، $a=-1$ و $b=1$. بیایید این ذوزنقه منحنی را ترسیم کنیم.

بیایید مساحت این ذوزنقه منحنی را پیدا کنیم.

$S=\int\limits_(-1)^(1)(\left(1-x^(2)\right)dx)=\int\limits_(-1)^(1)(1dx)-\int \limits_(-1)^(1)(x^(2)dx)=x|_(-1)^(1) - \ چپ.\frac(x^(3))(3)\راست|_ (-1)^(1)=$

$=(1-(-1))-\frac(1)(3)\left(1^(3)-(-1)^(3)\راست)=2 – \frac(1)(3) \left(1+1\right) = 2 – \frac(2)(3) = 1\frac(1)(3)$ (واحد$^(2)$).

نوع III: مساحت یک شکل محدود شده توسط تقاطع دو تابع غیر منفی پیوسته.این شکل یک ذوزنقه منحنی نخواهد بود، به این معنی که نمی توانید مساحت آن را با استفاده از فرمول (*) محاسبه کنید. چگونه بودن؟به نظر می رسد که مساحت این شکل را می توان به عنوان تفاوت بین مناطق ذوزنقه های منحنی محدود شده توسط تابع بالا و $y=0$ ($S_(uf)$) و تابع پایین و $y یافت. =0$ ($S_(lf)$)، که در آن نقش $x=a، \ x=b$ توسط مختصات $x$ نقاط تقاطع این توابع، یعنی.

$S=S_(uf)-S_(lf)$. (**)

مهمترین چیز هنگام محاسبه چنین مناطقی این است که با انتخاب توابع بالا و پایین "از دست ندهید".

به عنوان مثال، مساحت یک شکل را که با توابع $y=x^(2)$ و $y=x+6$ محدود شده است، پیدا کنید.

بیایید نقاط تقاطع این نمودارها را پیدا کنیم:

طبق قضیه ویتا،

$x_(1)=-2،\x_(2)=3.$

یعنی $a=-2،\b=3$. بیایید یک شکل بکشیم:

بنابراین، تابع بالا $y=x+6$ و تابع پایین $y=x^(2)$ است. سپس با استفاده از فرمول (*) $S_(uf)$ و $S_(lf)$ را پیدا می کنیم.

$S_(uf)=\int\limits_(-2)^(3)((x+6)dx)=\int\limits_(-2)^(3)(xdx)+\int\limits_(-2 )^(3)(6dx)=\چپ.\frac(x^(2))(2)\راست|_(-2)^(3) + 6x|_(-2)^(3)= 32 0.5$ (واحد$^(2)$).

$S_(lf)=\int\limits_(-2)^(3)(x^(2)dx)=\چپ.\frac(x^(3))(3)\راست|_(-2) ^(3) = \frac(35)(3)$ (واحد$^(2)$).

بیایید آنچه را که پیدا کردیم را با (**) جایگزین کنیم و دریافت کنیم:

$S=32.5-\frac(35)(3)= \frac(125)(6)$ (واحد$^(2)$).

نوع IV: مساحت یک شکل محدود شده توسط تابع(هایی) که شرایط غیر منفی را برآورده نمی کند.برای پیدا کردن مساحت چنین شکلی، باید در مورد محور $Ox$ متقارن باشید ( به عبارت دیگر،"منهای" را در جلوی توابع قرار دهید) ناحیه را نمایش دهید و با استفاده از روش های ذکر شده در انواع I - III ، مساحت ناحیه نمایش داده شده را پیدا کنید. این منطقه منطقه مورد نیاز خواهد بود. ابتدا، ممکن است مجبور شوید نقاط تقاطع نمودارهای تابع را پیدا کنید.

به عنوان مثال، مساحت یک شکل را که توسط نمودارهای توابع $y=x^(2)-1$ و $y=0$ محدود شده است، پیدا کنید.

بیایید نقاط تقاطع نمودارهای تابع را پیدا کنیم:

آن ها $a=-1$ و $b=1$. بیایید منطقه را ترسیم کنیم.

بیایید منطقه را به صورت متقارن نمایش دهیم:

$y=0 \ \پیکان راست \ y=-0=0$

$y=x^(2)-1 \ \پیکان راست \ y= -(x^(2)-1) = 1-x^(2)$.

نتیجه یک ذوزنقه منحنی است که توسط نمودار تابع $y=1-x^(2)$ و $y=0$ محدود شده است. این یک مشکل برای یافتن ذوزنقه منحنی نوع دوم است. ما قبلا آن را حل کرده ایم. پاسخ این بود: $S= 1\frac(1)(3)$ (واحد $^(2)$). این بدان معنی است که مساحت ذوزنقه منحنی مورد نیاز برابر است با:

$S=1\frac(1)(3)$ (واحد$^(2)$).

مساحت ذوزنقه منحنی

ذوزنقه منحنیشکلی است که توسط نموداری که در قسمت [ آ, ب] تابع پیوسته و غیر منفی f(ایکس) مختصات رسم شده در نقاط آو ب، و بخش محور گاو نربین نقاط آو ب(شکل 2 را ببینید).

اجازه دهید جمله زیر را ثابت کنیم.

ذوزنقه منحنی شکل مربع، مساحت است پ

اثبات. از آنجایی که پیوسته در بخش [ آ, ب] تابع قابل ادغام است، سپس برای هر عدد مثبت ε شما می توانید چنین پارتیشنی را مشخص کنید تیبخش [ آ, ب]، تفاوت در چیست اس - س < ε ، جایی که اسو س- به ترتیب مجموع بالا و پایین پارتیشن تی. ولی اسو سبه ترتیب برابر هستند اس دو اس من، جایی که اس دو اس من- نواحی شکل های پلکانی (چند ضلعی)، که اولی شامل یک ذوزنقه منحنی است، و دومی در یک ذوزنقه منحنی شکل (شکل 2 نیز این شکل های پلکانی را نشان می دهد). زیرا اس د - اس من < ε بنابراین، بر اساس قضیه 1، ذوزنقه منحنی مربعی است. از آنجایی که حد Δ → 0 مجموع بالا و پایین برابر است با س ≤ پ ≤ اس، سپس منطقه پذوزنقه منحنی را می توان با استفاده از فرمول (1) پیدا کرد.

اظهار نظر. اگر تابع f(ایکس) پیوسته و غیر مثبت در بخش [ آ, ب]، سپس مقدار انتگرال برابر است با مساحت ذوزنقه منحنی گرفته شده با علامت منفی، محدود شده توسط نمودار تابع. f(ایکس) ترتیب در نقاط آو بو بخش محور گاو نربین نقاط آو ب. بنابراین، اگر f(ایکس) تغییر علامت می دهد، سپس برابر است با مجموع مساحت ذوزنقه های منحنی واقع در بالا و پایین محور که با علامت معین گرفته شده است. گاو نرو نواحی اولی با علامت + و دومی با علامت - گرفته می شود.

مساحت یک بخش منحنی

اجازه دهید منحنی Lدر سیستم مختصات قطبی توسط معادله داده می شود r = r(θ ), α ≤ θ ≤ β (شکل 3 را ببینید)، و تابع r(θ ) پیوسته و غیر منفی در بخش [ α , β ]. یک شکل صاف که توسط یک منحنی محدود شده است Lو دو پرتو با محور قطبی زاویه می سازند α و β ، تماس خواهیم گرفت بخش منحنی.

اجازه دهید جمله زیر را ثابت کنیم. یک بخش منحنی یک شکل مربع، مساحت است پکه با استفاده از فرمول قابل محاسبه است

اثبات. پارتیشن را در نظر بگیرید تیبخش [ α , β ] نقطه ها α = θ 0 < θ 1 < ... < θ n = β و برای هر بخش جزئی [ θ من -1 , θ من] بخش های دایره ای را بسازید که شعاع آنها برابر با حداقل باشد r منو حداکثر آر منارزش های r(θ ) در بخش [ θ من -1 , θ من]. در نتیجه، دو شکل فن شکل به دست می‌آوریم که اولین آنها در بخش منحنی قرار دارد و دومی شامل بخش منحنی است (این شکل‌های فن شکل در شکل 3 نشان داده شده‌اند). مساحت و مساحت شکل های فن شکل نشان داده شده به ترتیب برابر و برابر است. توجه داشته باشید که اولین مورد از این مبالغ، مجموع پایین تر است سبرای یک تابع برای یک پارتیشن مشخص تیبخش [ α , β ]، و جمع دوم مجموع بالایی است اسبرای یک تابع و همان پارتیشن. از آنجایی که تابع در بخش [ α , β ]، سپس تفاوت می تواند به اندازه دلخواه کوچک باشد. به عنوان مثال، برای هر ثابت ε > 0 این تفاوت را می توان کوچکتر کرد ε /2. اکنون اجازه دهید یک چند ضلعی را در شکل پنکه ای شکل داخلی بنویسیم س منبا مساحت اس من، برای آن، و ما یک چند ضلعی در اطراف شکل فن شکل خارجی توصیف می کنیم س دحوزه اس د، برای کدام * . بدیهی است که اولین مورد از این چند ضلعی در یک بخش منحنی و دومی در اطراف آن محصور شده است. از آنجایی که نابرابری ها معتبر هستند

تعریف.تفاوت F (b) – F (a) را انتگرال تابع f (x) در بازه [a ; b ] و به صورت زیر نشان داده می شود: = F (b) – F (a) – فرمول نیوتن-لایب نیتس.

معنای هندسی انتگرال.

مساحت یک ذوزنقه منحنی که با یک نمودار مثبت پیوسته در بازه [a; b ] توابع f (x)، محور Ox و خطوط x=a و x=b:

محاسبه مساحت ها با استفاده از انتگرال

1. مساحت یک شکل محدود شده توسط یک نمودار منفی پیوسته در بازه [a; b ] توابع f (x)، محور Ox و خطوط x=a و x=b:

2. مساحت شکل محدود شده توسط نمودارهای توابع پیوسته f (x) و خطوط x=a, x= b:

3. مساحت شکل محدود شده توسط نمودارهای توابع پیوسته f (x) و:

4. مساحت شکل محدود شده توسط نمودارهای توابع پیوسته f (x) و محور Ox:

مسائل و تست های مبحث "انتگرال. محاسبه مساحت ها با استفاده از انتگرال"

• انتگرال

  درس: 4 تکلیف: 13 تست: 1

• محاسبه مساحت ها با استفاده از انتگرال - ضد مشتق و گرید انتگرال 11

  درس: 1 تکلیف: 10 تست: 1

• ضد مشتق - ضد مشتق و گرید انتگرال 11

  درس: 1 تکلیف: 11 تست: 1

• Planimetry: محاسبه طول و مساحت

  وظایف: 7

• محاسبات و تبدیل - آمادگی برای آزمون دولتی واحد در ریاضیات آزمون دولتی واحد در ریاضیات

  وظایف: 10

قبل از شروع محاسبه مساحت یک شکل محدود شده با خطوط داده شده، سعی کنید این شکل را در یک سیستم مختصات به تصویر بکشید. این کار حل مشکل را بسیار آسان تر می کند.

مطالعه مطالب نظری در مورد این موضوع به شما این فرصت را می دهد که بر مفاهیم ضد مشتق و انتگرال تسلط پیدا کنید، ارتباط بین آنها را درک کنید، بر ساده ترین تکنیک حساب انتگرال مسلط شوید و یاد بگیرید که انتگرال را برای محاسبه مساحت اعداد محدود شده توسط نمودارهای توابع به کار ببرید. .

مثال ها.

1. انتگرال را محاسبه کنید

راه حل:

پاسخ: 0.

2. مساحت شکل محدود شده با خطوط را پیدا کنید

آ) f(ایکس) = 2 ایکس – ایکس 2 و محور x

راه حل:نمودار تابع f(x) = 2x - x 2 یک سهمی است. راس: (1؛ 1).

پاسخ:(واحد مربع).

بدون تاریخ________

موضوع:ذوزنقه منحنی و مساحت آن ب

اهداف درس: یک ذوزنقه منحنی و مساحت آن را تعریف کنید، یاد بگیرید که مساحت یک ذوزنقه منحنی را محاسبه کنید.

در طول کلاس ها

1. لحظه سازمانی.

سلام کردن به دانش آموزان، بررسی آمادگی کلاس برای درس، سازماندهی توجه دانش آموزان، آشکار ساختن اهداف کلی درس و طرح آن.

2. مرحله بررسی تکالیف.

اهداف: ایجاد صحت، کامل بودن و آگاهی از انجام تکالیف توسط همه دانش آموزان، شناسایی شکاف ها در دانش و روش های فعالیت دانش آموزان. علل مشکلات را تعیین کنید و شکاف های پیدا شده را از بین ببرید.

3. مرحله به روز رسانی.

اهداف: اطمینان از انگیزه یادگیری دانش آموزان، مشارکت در فعالیت های مشترک برای تعیین اهداف درس. تجربه ذهنی دانش آموزان را به روز کنید.

بیایید مفاهیم و فرمول های اساسی را به خاطر بسپاریم.

تعریف.تابع y=f(x)، x (الف، ب)ضد مشتق تابع نامیده می شود y=f(x)، x (الف، ب)اگر برای همه ایکس (الف، ب)برابری برقرار است

اف (x)=f(x).

اظهار نظر.اگر f(ایکس)یک ضد مشتق برای تابع وجود دارد f(x)، سپس برای هر ثابت با, F(x)+Cهمچنین یک ضد مشتق برای f(x).

مشکل یافتن همه ضد مشتقات یک تابع f(x)انتگرال نامیده می شود و مجموعه تمام ضد مشتقات انتگرال نامعین برای تابع نامیده می شود. f(x)توسط dxو تعیین شده است

خواص زیر انجام می شود:

1. ;

2. اگر C=پس کنست
;

3.
.

اظهار نظر.در دروس ریاضیات مدرسه، اصطلاح "انتگرال نامعین" استفاده نمی شود، بلکه می گویند "مجموعه همه ضد مشتقات".

در اینجا جدولی از انتگرال های نامعین آمده است.

مثال 1.یک پاد مشتق برای یک تابع پیدا کنید
، از نقطه عبور می کند م(2;4).

راه حل.مجموعه ای از تمام ضد مشتقات یک تابع
یک انتگرال نامعین وجود دارد
. بیایید آن را با استفاده از خواص انتگرال 1 و 2 محاسبه کنیم. ما داریم:

ما دریافتیم که مجموعه تمام ضد مشتقات توسط یک خانواده از توابع داده می شود y=F(x)+C، به این معنا که y=x 3 – 2x+C، جایی که با- ثابت دلخواه

دانستن اینکه ضد مشتق از نقطه عبور می کند م(2;4)، مختصات آن را جایگزین عبارت قبلی کرده و پیدا کنید با.

4=2 3 –2 2+با  با=4–8+4; با=0.

پاسخ: F(x)=x 3 - 2ایکس- پاد مشتق مورد نظر.

4. شکل گیری مفاهیم و روش های جدید عمل.

اهداف: اطمینان از اینکه دانش آموزان مطالب مورد مطالعه را درک، درک و به خاطر بسپارند. اطمینان حاصل کنید که دانش‌آموزان بر روش‌های بازتولید مطالب مورد مطالعه تسلط دارند، درک فلسفی مفاهیم، ​​قوانین، قوانین و فرمول‌های در حال کسب را ارتقا می‌دهند. ایجاد صحت و آگاهی از مطالب مورد مطالعه توسط دانش آموزان، شناسایی شکاف ها در درک اولیه و انجام اصلاحات. اطمینان حاصل کنید که دانش آموزان تجربه ذهنی خود را با نشانه های دانش علمی مرتبط می کنند.

پیدا کردن مساحت شکل های هواپیما

مشکل یافتن مساحت یک شکل صفحه ارتباط نزدیکی با مشکل یافتن پاد مشتقات (ادغام) دارد. یعنی: مساحت ذوزنقه منحنی که توسط نمودار یک تابع محدود شده استy=f(x) (f(x)> 0) مستقیمx=a; x=b; y= 0، برابر با تفاوت بین مقادیر ضد مشتق برای تابعy=f(x) در نقاطب وآ :

S=F(b)–F(a)

اجازه دهید تعریف یک انتگرال معین را ارائه دهیم.

در باره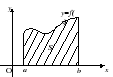
عزماجازه دهید تابع y=f(x)تعریف شده و قابل ادغام در بازه [ الف، ب] رهایش کن F(x)- برخی از نمونه های اولیه آن سپس شماره F(b)–F(a)به نام انتگرال از آقبل از بکارکرد f(x)و تعیین شده است

.

برابری
فرمول نیوتن-لایب نیتس نامیده می شود.

این فرمول مسئله یافتن مساحت یک شکل صفحه را با یک انتگرال مرتبط می کند.

به طور کلی، اگر شکل توسط نمودارهای تابع محدود شود y=f(x);y=g(x) (f(x)>g(x)) و مستقیم x=a;x=b، سپس مساحت آن برابر است با:

.

مثال 2.در کدام نقطه از نمودار تابع y=x 2 + 1 باید یک مماس رسم کنید تا از شکلی که توسط نمودار این تابع و خطوط مستقیم تشکیل شده است جدا شود. y= 0، x= 0، x= 1 ذوزنقه با بیشترین مساحت؟

راه حل.اجازه دهید م 0 (ایکس 0 ، y 0 ) – نقطه نمودار تابع y=x 2 + 1 که در آن مماس مورد نیاز رسم شده است.

بیایید معادله مماس را پیدا کنیم y=y 0 +f (ایکس 0 ) (x–x 0 ) .

ما داریم:

از همین رو

.

مساحت ذوزنقه را پیدا کنید OABC.

.

ب- نقطه تلاقی مماس با خط مستقیم x= 1 

کار به یافتن بزرگترین مقدار تابع کاهش یافت

اس(ایکس)=–x 2 +x+ 1 در بخش پیدا خواهیم کرد اس (ایکس)=– 2x+ 1. نقطه بحرانی را از شرط پیدا کنید اس (ایکس)= 0  x=.

می بینیم که تابع به بیشترین مقدار خود در at می رسد x=. پیدا خواهیم کرد
.

پاسخ:مماس باید در نقطه رسم شود
.

توجه داشته باشید که مشکل یافتن انتگرال بر اساس معنای هندسی آن اغلب با مشکل مواجه می شود. اجازه دهید با یک مثال نشان دهیم که چگونه این مشکل حل می شود.

مثال 4.با استفاده از معنای هندسی انتگرال، محاسبه کنید

آ )
; ب)
.

راه حل.

آ)
- برابر با مساحت ذوزنقه منحنی که با خطوط محدود شده است.

پ تبدیل کنیم

– نیمه بالایی دایره با مرکز آر(1;0) و شعاع R= 1.

از همین رو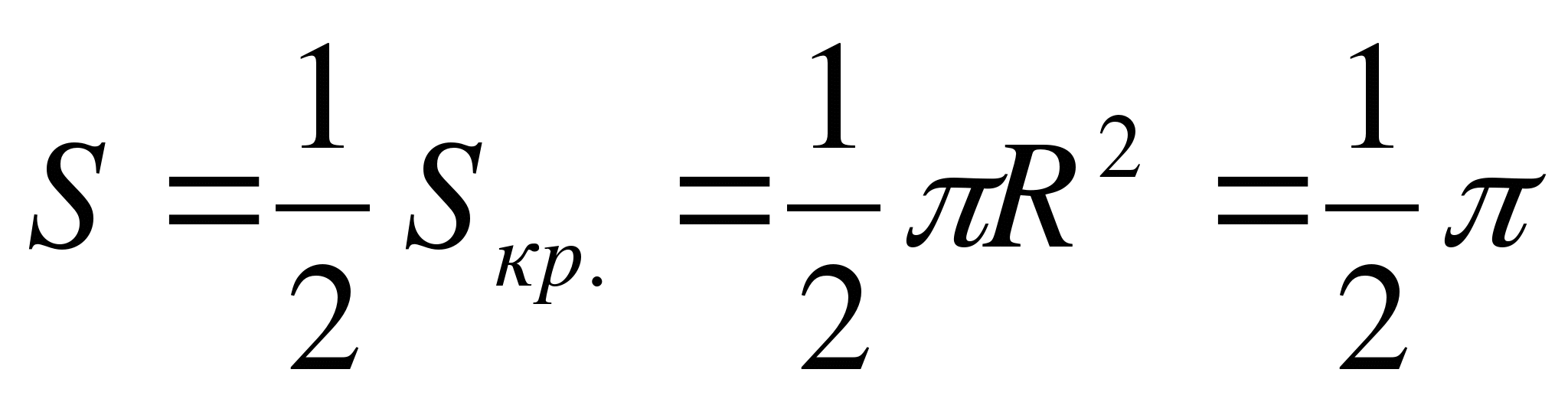
.

پاسخ:
.

ب) با استدلال مشابه، بیایید یک منطقه محدود شده توسط نمودارهای .2 بسازیم – 2x+ 2، مماس بر آن در نقاط آ
, ب(4;2)

y=–9ایکس- 59، سهمی y= 3ایکس 2 + تبر + 1، اگر مشخص شود که مماس بر سهمی در نقطه است x=– 2 با محور است گاو نراندازه زاویه arctg 6.

پیدا کردن آ، اگر مشخص شود که مساحت یک ذوزنقه منحنی با خطوط محدود شده است y= 3ایکس 3 + 2x، x=a، y= 0 برابر است با یک

کوچکترین مساحت یک شکل محدود به سهمی را پیدا کنید y=x 2 + 2ایکس- 3 و مستقیم y=kx+ 1.

6.مرحله اطلاعات تکلیف.

اهداف: اطمینان از اینکه دانش آموزان هدف، محتوا و روش انجام تکالیف را درک می کنند. شماره 18، 19،20،21 فرد

7. جمع بندی درس.

هدف: ارائه یک ارزیابی کیفی از کار کلاس و تک تک دانش آموزان.