Konceptet med en krökt trapets. Ämne: Krökt trapets och dess område. Bildande av nya koncept och handlingsmetoder

En figur som avgränsas av grafen för en kontinuerlig icke-negativ funktion $f(x)$ på segmentet $$ och linjerna $y=0, \ x=a$ och $x=b$ kallas en kurvlinjär trapets.

Arean av den motsvarande krökta trapetsen beräknas med formeln:

$S=\int\limits_(a)^(b)(f(x)dx).$ (*)

Vi kommer villkorligt att dela upp problem för att hitta området för en kurvlinjär trapets i $4$-typer. Låt oss titta på varje typ mer detaljerat.

Typ I: en böjd trapets anges uttryckligen. Använd sedan omedelbart formeln (*).

Hitta till exempel arean av en krökt trapets som avgränsas av grafen för funktionen $y=4-(x-2)^(2)$ och linjerna $y=0, \ x=1$ och $x =3$.

Låt oss rita denna böjda trapets.

Med formeln (*) hittar vi arean av denna krökta trapets.

$S=\int\limits_(1)^(3)(\left(4-(x-2)^(2)\right)dx)=\int\limits_(1)^(3)(4dx)- \int\limits_(1)^(3)((x-2)^(2)dx)=4x|_(1)^(3) – \left.\frac((x-2)^(3) )(3)\höger|_(1)^(3)=$

$=4(3-1)-\frac(1)(3)\left((3-2)^(3)-(1-2)^(3)\right)=4 \cdot 2 – \frac (1)(3)\vänster((1)^(3)-(-1)^(3)\höger) = 8 – \frac(1)(3)(1+1) =$

$=8-\frac(2)(3)=7\frac(1)(3)$ (enheter$^(2)$).

Typ II: den krökta trapetsen anges implicit. I det här fallet är de raka linjerna $x=a, \ x=b$ vanligtvis inte specificerade eller delvis specificerade. I det här fallet måste du hitta skärningspunkterna för funktionerna $y=f(x)$ och $y=0$. Dessa poäng kommer att vara poäng $a$ och $b$.

Hitta till exempel arean av en figur som avgränsas av graferna för funktionerna $y=1-x^(2)$ och $y=0$.

Låt oss hitta skärningspunkterna. För att göra detta likställer vi funktionernas högra sida.

Alltså $a=-1$ och $b=1$. Låt oss rita denna böjda trapets.

Låt oss hitta området för denna böjda trapets.

$S=\int\limits_(-1)^(1)(\left(1-x^(2)\right)dx)=\int\limits_(-1)^(1)(1dx)-\int \limits_(-1)^(1)(x^(2)dx)=x|_(-1)^(1) – \left.\frac(x^(3))(3)\right|_ (-1)^(1)=$

$=(1-(-1))-\frac(1)(3)\left(1^(3)-(-1)^(3)\right)=2 – \frac(1)(3) \left(1+1\right) = 2 – \frac(2)(3) = 1\frac(1)(3)$ (enheter$^(2)$).

Typ III: arean av en figur som begränsas av skärningspunkten mellan två kontinuerliga icke-negativa funktioner. Denna figur kommer inte att vara en böjd trapets, vilket betyder att du inte kan beräkna dess area med formeln (*). Hur man är? Det visar sig att arean av denna figur kan hittas som skillnaden mellan områdena av kurvlinjära trapetser som begränsas av den övre funktionen och $y=0$ ($S_(uf)$), och den nedre funktionen och $y =0$ ($S_(lf)$), där rollen för $x=a, \ x=b$ spelas av $x$-koordinaterna för skärningspunkterna för dessa funktioner, dvs.

$S=S_(uf)-S_(lf)$. (**)

Det viktigaste när man beräknar sådana områden är att inte "missa" med valet av de övre och nedre funktionerna.

Hitta till exempel arean av en figur som avgränsas av funktionerna $y=x^(2)$ och $y=x+6$.

Låt oss hitta skärningspunkterna för dessa grafer:

Enligt Vietas teorem,

$x_(1)=-2,\x_(2)=3.$

Det vill säga $a=-2,\b=3$. Låt oss rita en figur:

Den översta funktionen är alltså $y=x+6$, och den nedre funktionen är $y=x^(2)$. Därefter hittar vi $S_(uf)$ och $S_(lf)$ med hjälp av formel (*).

$S_(uf)=\int\limits_(-2)^(3)((x+6)dx)=\int\limits_(-2)^(3)(xdx)+\int\limits_(-2) )^(3)(6dx)=\vänster.\frac(x^(2))(2)\höger|_(-2)^(3) + 6x|_(-2)^(3)= 32 .5$ (enheter$^(2)$).

$S_(lf)=\int\limits_(-2)^(3)(x^(2)dx)=\vänster.\frac(x^(3))(3)\höger|_(-2) ^(3) = \frac(35)(3)$ (enheter$^(2)$).

Låt oss ersätta det vi hittade med (**) och få:

$S=32.5-\frac(35)(3)= \frac(125)(6)$ (enheter$^(2)$).

Typ IV: arean av en figur som begränsas av en funktion(er) som inte uppfyller icke-negativitetsvillkoret. För att hitta arean för en sådan figur måste du vara symmetrisk kring $Ox$-axeln ( med andra ord, sätt "minus" framför funktionerna) visa området och, med hjälp av metoderna som beskrivs i typ I – III, hitta området för det visade området. Detta område kommer att vara det område som krävs. Först kan du behöva hitta skärningspunkterna för funktionsgraferna.

Hitta till exempel arean av en figur som avgränsas av graferna för funktionerna $y=x^(2)-1$ och $y=0$.

Låt oss hitta skärningspunkterna för funktionsgraferna:

de där. $a=-1$ och $b=1$. Låt oss rita området.

Låt oss visa området symmetriskt:

$y=0 \ \Högerpil \ y=-0=0$

$y=x^(2)-1 \ \Högerpil \ y= -(x^(2)-1) = 1-x^(2)$.

Resultatet är en kurvlinjär trapets som begränsas av grafen för funktionen $y=1-x^(2)$ och $y=0$. Detta är ett problem att hitta en krökt trapets av den andra typen. Vi har redan löst det. Svaret var: $S= 1\frac(1)(3)$ (enheter $^(2)$). Detta betyder att arean av den erforderliga krökta trapetsen är lika med:

$S=1\frac(1)(3)$ (enheter$^(2)$).

Area av en krökt trapets

Krökt trapetsär en figur som avgränsas av en graf som ges på segmentet [ a, b] kontinuerlig och icke-negativ funktion f(x), ordinator ritade vid punkter a Och b, och axelsegment Oxe mellan punkter a Och b(se fig. 2).

Låt oss bevisa följande påstående.

En böjd trapets är en kvadratisk figur, area P

Bevis. Eftersom kontinuerligt på segmentet [ a, b] funktionen är integrerbar, sedan för ett positivt tal ε du kan ange en sådan partition T segmentet [ a, b], vad är skillnaden S - s < ε , Var S Och s- den övre och den nedre summan av partitionen, respektive T. Men S Och sär likvärdiga respektive S d Och S i, Var S d Och S i- områden med stegformade figurer (polygoner), av vilka den första innehåller en krökt trapets, och den andra finns i en krökt trapets (fig. 2 visar också dessa stegformade figurer). Därför att S d - S i < ε , då, i kraft av sats 1, är den kurvlinjära trapetsen kvadratisk. Eftersom gränsen för Δ → 0 för de övre och nedre summorna är lika med s ≤ P ≤ S, sedan området P krökt trapets kan hittas med formel (1).

Kommentar. Om funktionen f(x) är kontinuerlig och icke-positiv på segmentet [ a, b], då är värdet på integralen lika med arean av den krökta trapetsen taget med ett negativt tecken, begränsat av funktionens graf f(x), ordinater vid punkter a Och b och axelsegment Oxe mellan punkter a Och b. Därför, om f(x) byter tecken, då är det lika med summan av arean av kurvlinjära trapetser som ligger ovanför och under axeln taget med ett visst tecken Oxe, och områdena för det förra tas med +-tecknet och för det senare med -tecknet.

Area av en krökt sektor

Låt kurvan L ges i det polära koordinatsystemet av ekvationen r = r(θ ), α ≤ θ ≤ β (se fig. 3), och funktionen r(θ ) är kontinuerlig och icke-negativ på segmentet [ α , β ]. En platt figur avgränsad av en kurva L och två strålar som bildar vinklar med polaxeln α Och β , vi ringer kurvlinjär sektor.

Låt oss bevisa följande påstående. En kurvlinjär sektor är en kvadratisk figur, area P som kan beräknas med hjälp av formeln

Bevis. Tänk på partitionen T segmentet [ α , β ] prickar α = θ 0 < θ 1 < ... < θ n = β och för varje delsegment [ θ i -1 , θ i] konstruera cirkulära sektorer vars radier är lika med minimum r i och maximalt R i värden r(θ ) på segmentet [ θ i -1 , θ i]. Som ett resultat får vi två solfjäderformade figurer, varav den första finns i den kurvlinjära sektorn och den andra innehåller den kurvlinjära sektorn (dessa solfjäderformade figurer visas i fig. 3). Ytorna för och av de angivna solfjäderformade figurerna är lika med respektive. Observera att den första av dessa summor är den lägre summan s för en funktion för en specificerad partition T segmentet [ α , β ], och den andra summan är den översta summan S för samma funktion och samma partition. Eftersom funktionen är integrerbar på segmentet [ α , β ], så kan skillnaden vara så liten som önskas. Till exempel för alla fasta ε > 0 denna skillnad kan göras mindre ε /2. Låt oss nu skriva in en polygon i den inre solfjäderformade figuren F i med område S i, för vilket , och vi beskriver en polygon runt den yttre solfjäderformade figuren F d område S d, för vilka * . Uppenbarligen är den första av dessa polygoner inskriven i en kurvlinjär sektor, och den andra är omskriven runt den. Eftersom ojämlikheterna är sanna

Definition. Skillnaden F (b) – F (a) kallas integralen av funktionen f (x) på intervallet [ a ; b ] och betecknas enligt följande: = F (b) – F (a) – Newton-Leibniz formel.

Integralens geometriska betydelse.

Arean av en krökt trapets som begränsas av en kontinuerlig positiv graf på intervallet [a; b ] funktioner f (x), Ox-axeln och linjerna x=a och x= b:

Beräkna ytor med hjälp av en integral.

1. Arean av en figur som begränsas av en kontinuerlig negativ graf på intervallet [a; b ] funktioner f (x), Ox-axeln och linjerna x=a och x= b:

2. Arean av figuren som begränsas av graferna för kontinuerliga funktioner f (x) och linjerna x=a, x= b:

3. Arean av figuren som begränsas av graferna för kontinuerliga funktioner f (x) och:

4. Arean av figuren som begränsas av graferna för kontinuerliga funktioner f (x) och Ox-axeln:

Problem och tester på ämnet "Integral. Beräkning av arealer med hjälp av integralen"

• Väsentlig

  Lektioner: 4 uppgifter: 13 prov: 1

• Beräkna ytor med integraler - Antiderivat och integral grad 11

  Lektioner: 1 inlämningsuppgifter: 10 prov: 1

• Antiderivat - Antiderivat och integral grad 11

  Lektioner: 1 inlämningsuppgifter: 11 prov: 1

• Planimetri: beräkning av längder och ytor

  Arbetsuppgifter: 7

• Beräkningar och omvandlingar - Förberedelse för Unified State Examination in Mathematics Unified State Examination in Mathematics

  Arbetsuppgifter: 10

Innan du börjar beräkna arean av en figur som avgränsas av givna linjer, försök att avbilda denna figur i ett koordinatsystem. Detta kommer att göra det mycket lättare att lösa problemet.

Att studera teoretiska material om detta ämne ger dig möjlighet att behärska begreppen antiderivat och integral, förstå sambandet mellan dem, behärska den enklaste tekniken för integralkalkyl och lära dig att tillämpa integralen för att beräkna områdena av figurer som begränsas av grafer över funktioner .

Exempel.

1. Beräkna integralen

Lösning:

Svar: 0.

2. Hitta arean av figuren som avgränsas av linjerna

a) f(x) = 2 X – X 2 och x-axeln

Lösning: Grafen för funktionen f(x) = 2x - x 2 är en parabel. Vertex: (1; 1).

Svar:(kvm enheter).

Inget datum________

Ämne:Krökt trapets och dess område b

Lektionens mål: Definiera en böjd trapets och dess area, lär dig att beräkna arean av en böjd trapets.

UNDER KLASSERNA

1. Organisatoriskt ögonblick.

Att hälsa på eleverna, kontrollera klassens redo för lektionen, organisera elevernas uppmärksamhet, avslöja lektionens allmänna mål och dess plan.

2. Läxkontrollstadiet.

Mål: Att fastställa riktigheten, fullständigheten och medvetenheten om hur läxor utförs av alla elever, att identifiera luckor i elevernas kunskaper och metoder för aktivitet. Bestäm orsakerna till svårigheter och eliminera eventuella luckor som finns.

3. Uppdateringsstadium.

Mål: säkerställa motivationen för skolbarns lärande, inkludering i gemensamma aktiviteter för att fastställa målen för lektionen. Uppdatera elevernas subjektiva upplevelse.

Låt oss komma ihåg de grundläggande begreppen och formlerna.

Definition. Fungera y=f(x), x (a,b), kallas antiderivatan av funktionen y=f(x), x (a,b), om för alla x (a,b) jämställdhet gäller

F (x)=f(x).

Kommentar. Om f(x) det finns en antiderivata för funktionen f(x), sedan för någon konstant MED, F(x)+Cär också ett antiderivat för f(x).

Problemet med att hitta alla antiderivator av en funktion f(x) kallas integration, och mängden av alla antiderivator kallas den obestämda integralen för funktionen f(x) Förbi dx och är utsedd

Följande fastigheter äger rum:

1 . ;

2 . Om C= Konst alltså
;

3.
.

Kommentar. I skolans matematikkurser används inte termen "obestämd integral" utan istället säger de "uppsättningen av alla antiderivator."

Här är en tabell med obestämda integraler.

Exempel 1. Hitta en antiderivata för en funktion
, passerar genom punkten M(2;4).

Lösning. Uppsättningen av alla antiderivator av en funktion
det finns en obestämd integral
. Låt oss beräkna det med hjälp av egenskaperna för integralen 1 och 2. Vi har:

Vi fann att uppsättningen av alla antiderivat ges av en familj av funktioner y=F(x)+C, det är y=x 3 – 2x+C, Var MED– godtycklig konstant.

Att veta att antiderivatan passerar genom punkten M(2;4), ersätt dess koordinater med föregående uttryck och hitta MED.

4=2 3 –2 2+MED  MED=4–8+4; MED=0.

Svar: F(x)=x 3 - 2x- det önskade antiderivatet.

4. Bildande av nya koncept och handlingsmetoder.

Mål: Att säkerställa att eleverna uppfattar, förstår och kommer ihåg materialet som studeras. Se till att eleverna behärskar metoderna för att reproducera det studerade materialet, främja filosofisk förståelse av de begrepp, lagar, regler och formler som tillägnas. Att fastställa korrektheten och medvetenheten om det studerade materialet av studenter, att identifiera luckor i primär förståelse och att utföra korrigeringar. Se till att eleverna korrelerar sin subjektiva upplevelse med tecken på vetenskaplig kunskap.

Hitta områdena för plana figurer

Problemet med att hitta arean av en plan figur är nära relaterat till problemet med att hitta antiderivat (integration). Nämligen: arean av en kurvlinjär trapets som begränsas av grafen för en funktiony=f(x) (f(x)> 0) raktx=a; x=b; y= 0, lika med skillnaden mellan värdena på antiderivatan för funktioneny=f(x) på punkterb Ocha :

S=F(b)–F(a)

Låt oss ge definitionen av en bestämd integral.

HANDLA OM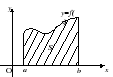
definition. Låt funktionen y=f(x) definierad och integrerbar på intervallet [ a,b] släpp det F(x)- några av dess prototyper. Sedan numret F(b)–F(a) kallas integralen av A innan b funktioner f(x) och är utsedd

.

Jämlikhet
kallas Newton–Leibniz-formeln.

Denna formel kopplar ihop problemet med att hitta arean av en plan figur med en integral.

I allmänhet, om figuren begränsas av funktionsdiagram y=f(x);y=g(x) (f(x)>g(x)) och rak x=a;x=b, då är dess yta lika med:

.

Exempel 2. Vid vilken punkt i grafen för funktionen y=x 2 + 1 måste du rita en tangent så att den skär av från figuren som bildas av grafen för denna funktion och raka linjer y= 0, x= 0, x= 1 trapets med störst yta?

Lösning. Låta M 0 (x 0 ,y 0 ) – punkt på funktionsgrafen y=x 2 + 1, där den erforderliga tangenten är ritad.

Låt oss hitta tangentekvationen y=y 0 +f (x 0 )(x–x 0 ) .

Vi har:

Det är därför

.

Hitta arean för trapetsen OABC.

.

B– skärningspunkten mellan tangenten och den räta linjen x= 1 

Uppgiften reducerades till att hitta det största värdet av funktionen

S(x)=–x 2 +x+ 1 på segmentet. Vi hittar S (x)=– 2x+ 1. Hitta den kritiska punkten från tillståndet S (x)= 0  x=.

Vi ser att funktionen når sitt största värde vid x=. Vi hittar
.

Svar: tangenten måste dras vid punkten
.

Observera att problemet med att hitta en integral baserat på dess geometriska betydelse ofta stöter på. Låt oss visa med ett exempel hur detta problem löses.

Exempel 4. Beräkna med hjälp av integralens geometriska betydelse

A )
; b)
.

Lösning.

A)
– lika med arean av en krökt trapets som avgränsas av linjer.

P låt oss förvandla

– den övre halvan av cirkeln med mitten R(1;0) och radie R= 1.

Det är därför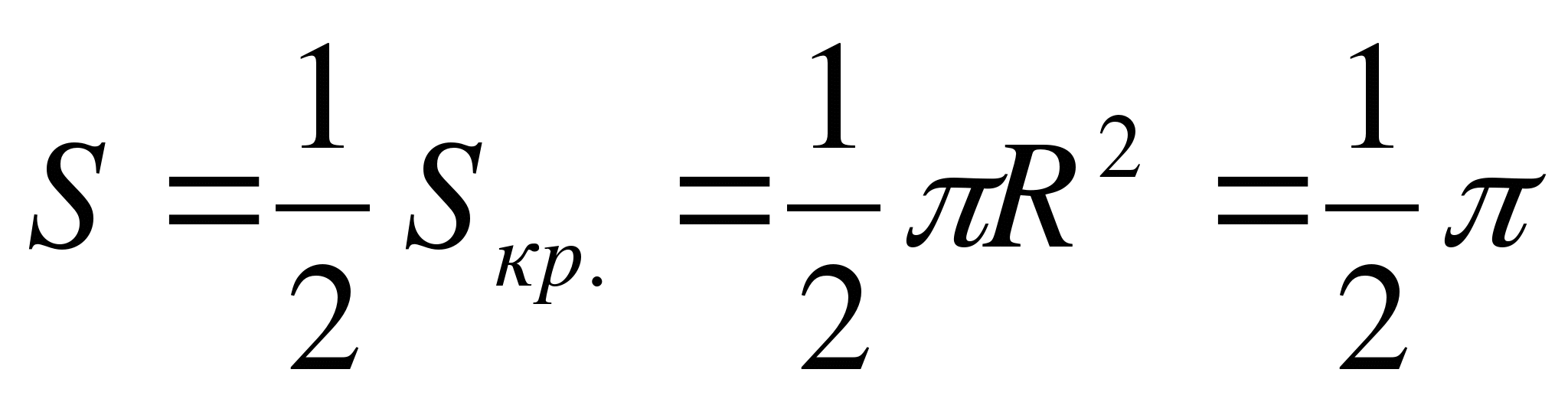
.

Svar:
.

b) Med liknande argument, låt oss konstruera ett område som begränsas av grafer .2 – 2x+ 2, tangent till den vid punkter A
, B(4;2)

y=–9x– 59, parabel y= 3x 2 +ax+ 1, om det är känt att tangenten till parabeln vid punkten x=– 2 är med axel Oxe vinkelstorlek arctg 6.

Hitta A, om det är känt att området av en krökt trapets avgränsas av linjer y= 3x 3 + 2x, x=a, y= 0 är lika med en.

Hitta den minsta ytan av en figur som avgränsas av en parabel y=x 2 + 2x– 3 och rak y=kx+ 1.

6. Läxinformationsstadiet.

Mål: Att säkerställa att eleverna förstår syftet, innehållet och metoderna för att göra läxor. Nr 18, 19,20,21 udda

7. Sammanfattning av lektionen.

Mål: Att ge en kvalitativ bedömning av klassens och enskilda elevers arbete.