Муруй трапецын тухай ойлголт. Сэдэв: Муруй шугаман трапец ба түүний талбай. Үйл ажиллагааны шинэ ойлголт, арга барилыг бий болгох

$$ хэрчим ба $y=0, \ x=a$, $x=b$ шулуунууд дээрх $f(x)$ тасралтгүй сөрөг бус функцийн графикаар хязгаарлагдсан дүрсийг муруй шугаман трапец гэнэ.

Харгалзах муруй шугаман трапецын талбайг дараахь томъёогоор тооцоолно.

$S=\int\limits_(a)^(b)(f(x)dx).$ (*)

Бид муруй шугаман трапецын талбайг олохын тулд асуудлыг нөхцлөөр хуваана $4$ төрөлд. Төрөл бүрийг илүү нарийвчлан авч үзье.

I төрөл: муруй трапецийг тодорхой зааж өгсөн.Дараа нь нэн даруй томъёог (*) хэрэглэнэ.

Жишээлбэл, $y=4-(x-2)^(2)$ функцийн график болон $y=0, \ x=1$, $x шугамуудаар хязгаарлагдсан муруйн трапецын талбайг ол. =3 доллар.

Энэ муруй трапецийг зурцгаая.

Томъёог (*) ашиглан бид энэ муруйн трапецын талбайг олно.

$S=\int\limits_(1)^(3)(\left(4-(x-2)^(2)\right)dx)=\int\limits_(1)^(3)(4dx)- \int\limits_(1)^(3)((x-2)^(2)dx)=4x|_(1)^(3) – \left.\frac((x-2)^(3) )(3)\баруун|_(1)^(3)=$

$=4(3-1)-\frac(1)(3)\зүүн((3-2)^(3)-(1-2)^(3)\баруун)=4 \cdot 2 – \frac (1)(3)\зүүн((1)^(3)-(-1)^(3)\баруун) = 8 – \frac(1)(3)(1+1) =$

$=8-\frac(2)(3)=7\frac(1)(3)$ (нэгж$^(2)$).

II төрөл: муруй трапецийг далд хэлбэрээр зааж өгсөн.Энэ тохиолдолд $x=a, \ x=b$ шулуун шугамууд ихэвчлэн тодорхойлогдоогүй эсвэл хэсэгчлэн тодорхойлогддоггүй. Энэ тохиолдолд $y=f(x)$ ба $y=0$ функцүүдийн огтлолцох цэгүүдийг олох хэрэгтэй. Эдгээр цэгүүд нь $a$ ба $b$ цэгүүд болно.

Жишээлбэл, $y=1-x^(2)$ ба $y=0$ функцуудын графикаар хязгаарлагдсан зургийн талбайг ол.

Уулзалтын цэгүүдийг олцгооё. Үүнийг хийхийн тулд бид функцүүдийн баруун талыг тэгшитгэдэг.

Тиймээс $a=-1$ ба $b=1$. Энэ муруй трапецийг зурцгаая.

Энэ муруй трапецын талбайг олцгооё.

$S=\int\limits_(-1)^(1)(\зүүн(1-x^(2)\баруун)dx)=\int\limits_(-1)^(1)(1dx)-\int \хязгаар_(-1)^(1)(x^(2)dx)=x|_(-1)^(1) – \left.\frac(x^(3))(3)\баруун|_ (-1)^(1)=$

$=(1-(-1))-\frac(1)(3)\зүүн(1^(3)-(-1)^(3)\баруун)=2 – \frac(1)(3) \left(1+1\right) = 2 – \frac(2)(3) = 1\frac(1)(3)$ (нэгж$^(2)$).

III төрөл: хоёр тасралтгүй сөрөг бус функцийн огтлолцолоор хязгаарлагдсан зургийн талбай.Энэ зураг нь муруй трапец биш бөгөөд энэ нь (*) томъёог ашиглан түүний талбайг тооцоолох боломжгүй гэсэн үг юм. Яаж байх вэ?Энэ зургийн талбайг дээд функц ба $y=0$ ($S_(uf)$) ба доод функц ба $y-ээр хязгаарлагдсан муруй шугаман трапецын талбайн хоорондох зөрүүгээр олж болно. =0$ ($S_(lf)$), энд $x=a, \ x=b$-ын үүргийг эдгээр функцүүдийн огтлолцох цэгүүдийн $x$ координат гүйцэтгэдэг, i.e.

$S=S_(uf)-S_(lf)$. (**)

Ийм талбайг тооцоолохдоо хамгийн чухал зүйл бол дээд ба доод функцийг сонгохдоо "алдагдах"гүй байх явдал юм.

Жишээлбэл, $y=x^(2)$ ба $y=x+6$ функцээр хязгаарлагдсан зургийн талбайг ол.

Эдгээр графикуудын огтлолцох цэгүүдийг олцгооё.

Виетийн теоремын дагуу.

$x_(1)=-2,\ x_(2)=3.$

Энэ нь $a=-2,\b=3$ гэсэн үг. Зураг зуръя:

Тиймээс дээд функц нь $y=x+6$, доод функц нь $y=x^(2)$ байна. Дараа нь бид (*) томъёог ашиглан $S_(uf)$ болон $S_(lf)$-г олно.

$S_(uf)=\int\limits_(-2)^(3)((x+6)dx)=\int\limits_(-2)^(3)(xdx)+\int\limits_(-2) )^(3)(6dx)=\left.\frac(x^(2))(2)\баруун|_(-2)^(3) + 6x|_(-2)^(3)= 32 .5$ (нэгж$^(2)$).

$S_(lf)=\int\limits_(-2)^(3)(x^(2)dx)=\left.\frac(x^(3))(3)\баруун|_(-2) ^(3) = \frac(35)(3)$ (нэгж$^(2)$).

Олсон зүйлээ (**) гэж орлуулаад дараахийг авъя:

$ S = 32.5- \ frac (35) (3) = \ frac (125) (6) $ (нэгж $ ^ (2) $).

IV төрөл: сөрөг бус нөхцөлийг хангаагүй функц(ууд)-аар хязгаарлагдсан зургийн талбай.Ийм дүрсийн талбайг олохын тулд та $Ox $ тэнхлэгт тэгш хэмтэй байх хэрэгтэй ( Өөрөөр хэлбэл,функцүүдийн өмнө "хасах" тэмдэг тавь) талбарыг харуулах ба I - III төрөлд заасан аргуудыг ашиглан харуулсан хэсгийн талбайг ол. Энэ талбай нь шаардлагатай талбай байх болно. Эхлээд та функцийн графикуудын огтлолцох цэгүүдийг олох хэрэгтэй.

Жишээлбэл, $y=x^(2)-1$ ба $y=0$ функцуудын графикаар хязгаарлагдсан зургийн талбайг ол.

Функцийн графикуудын огтлолцох цэгүүдийг олцгооё.

тэдгээр. $a=-1$, $b=1$. Талбайг зурцгаая.

Талбайг тэгш хэмтэйгээр харуулъя:

$y=0 \ \Баруун сум \ y=-0=0$

$y=x^(2)-1 \ \Баруун сум \ y= -(x^(2)-1) = 1-x^(2)$.

Үүний үр дүнд $y=1-x^(2)$ ба $y=0$ функцийн графикаар хязгаарлагдсан муруй шугаман трапец байна. Энэ нь хоёр дахь төрлийн муруй трапецийг олох асуудал юм. Бид үүнийг аль хэдийн шийдсэн. Хариулт нь: $S= 1\frac(1)(3)$ (нэгж $^(2)$). Энэ нь шаардлагатай муруй шугаман трапецын талбай нь дараахь хэмжээтэй тэнцүү байна гэсэн үг юм.

$S=1\frac(1)(3)$ (нэгж$^(2)$).

Муруй трапецын талбай

Муруй шугаман трапецсегмент дээр өгөгдсөн графикаар хязгаарлагдсан дүрс юм [ а, б] тасралтгүй ба сөрөг бус функц е(x), цэгүүдэд зурсан ординатууд аТэгээд б, ба тэнхлэгийн сегмент Үхэрцэгүүдийн хооронд аТэгээд б(2-р зургийг үз).

Дараах мэдэгдлийг баталцгаая.

Муруй трапец бол дөрвөлжин дүрс, талбай юм П

Баталгаа. Сегмент дээр үргэлжилсэн тул [ а, б] функц нь интегралдах боломжтой, дараа нь дурын эерэг тооны хувьд ε Та ийм хуваалтыг зааж өгч болно Тсегмент [ а, б], ялгаа нь юу вэ С - с < ε , Хаана СТэгээд с- хуваалтын дээд ба доод нийлбэрүүд Т. Гэхдээ СТэгээд стус тус тэнцүү байна С гТэгээд С би, Хаана С гТэгээд С би- шаталсан дүрсүүдийн (олон өнцөгт) хэсгүүдийн эхнийх нь муруйн трапец, хоёр дахь нь муруйн трапец хэлбэрээр агуулагддаг (Зураг 2-т эдгээр шаталсан дүрсийг мөн харуулав). Учир нь С г - С би < ε , тэгвэл 1-р теоремын дагуу муруйн трапец дөрвөлжин хэлбэртэй байна. Дээд ба доод нийлбэрийн Δ → 0-ийн хязгаар нь тэнцүү байна с ≤ П ≤ С, дараа нь талбай Пмуруй трапецийг (1) томъёог ашиглан олж болно.

Сэтгэгдэл. Хэрэв функц е(x) сегмент дээр тасралтгүй ба эерэг биш байна [ а, б], тэгвэл интегралын утга нь функцийн графикаар хязгаарлагдсан сөрөг тэмдгээр авсан муруйн трапецын талбайтай тэнцүү байна. е(x), цэг дээрх ординатууд аТэгээд бба тэнхлэгийн сегмент Үхэрцэгүүдийн хооронд аТэгээд б. Тиймээс, хэрэв е(x) тэмдэг өөрчлөгдвөл тодорхой тэмдгээр авсан тэнхлэгээс дээш ба доор байрлах муруйн трапецын талбайн нийлбэртэй тэнцүү байна. Үхэр, мөн эхнийх нь талбайг + тэмдгээр, сүүлийнх нь - тэмдгээр авдаг.

Муруй салбарын талбай

Муруй байг Лтуйлын координатын системд тэгшитгэлээр өгөгдсөн r = r(θ ), α ≤ θ ≤ β (3-р зургийг үз), функц r(θ ) сегмент дээр тасралтгүй ба сөрөг бус байна [ α , β ]. Муруйгаар хязгаарлагдсан хавтгай дүрс Лба туйлын тэнхлэгтэй өнцөг үүсгэсэн хоёр цацраг α Тэгээд β , бид залгах болно муруйн салбар.

Дараах мэдэгдлийг баталцгаая. Муруй шугаман сектор нь дөрвөлжин дүрс, талбай юм Птомъёог ашиглан тооцоолж болно

Баталгаа. Хуваалтыг авч үзье Тсегмент [ α , β ] цэгүүд α = θ 0 < θ 1 < ... < θ n = β мөн хэсэгчилсэн сегмент бүрийн хувьд [ θ би -1 , θ би] радиус нь хамгийн багатай тэнцүү дугуй секторуудыг байгуулна r биба дээд тал нь Р биүнэт зүйлс r(θ ) сегмент дээр [ θ би -1 , θ би]. Үүний үр дүнд бид хоёр сэнс хэлбэртэй дүрсийг олж авдаг бөгөөд тэдгээрийн эхнийх нь муруйн секторт, хоёр дахь нь муруйн салбарыг агуулдаг (эдгээр сэнс хэлбэртэй дүрсийг 3-р зурагт үзүүлэв). Заасан сэнс хэлбэртэй дүрсүүдийн талбайнууд нь тэнцүү байна. Эдгээр нийлбэрүүдийн эхнийх нь доод нийлбэр гэдгийг анхаарна уу сзаасан хуваалтын функцийн хувьд Тсегмент [ α , β ], хоёр дахь нийлбэр нь дээд нийлбэр юм Сижил функц, ижил хуваалтын хувьд. Функц нь [ сегмент дээр интегралдах боломжтой тул [ α , β ], тэгвэл ялгаа нь хүссэн хэмжээгээр бага байж болно. Жишээ нь, ямар ч тогтмол ε > 0 энэ ялгааг багасгаж болно ε /2. Одоо дотоод сэнс хэлбэртэй дүрсэнд олон өнцөгт дүрс бичье Q биталбайтай С би, үүний төлөө бид гадаад сэнс хэлбэртэй дүрсийг тойрсон олон өнцөгтийг дүрсэлдэг Q гталбай С г, Үүний төлөө * . Мэдээжийн хэрэг, эдгээр олон өнцөгтүүдийн эхнийх нь муруй шугаман хэсэгт, хоёр дахь нь эргэн тойронд нь хүрээлэгдсэн байдаг. Тэгш бус байдал нь хүчинтэй учраас

Тодорхойлолт. F (b) – F (a) ялгааг f (x) функцийн интеграл гэж нэрлэдэг [ a ; b ] ба дараах байдлаар тэмдэглэнэ: = F (b) – F (a) – Ньютон-Лейбницийн томъёо.

Интегралын геометрийн утга.

[a; b ] функц f (x), Ox тэнхлэг ба x=a ба x= b шулуунууд:

Интеграл ашиглан талбайг тооцоолох.

1. [a; интервал дээр тасралтгүй сөрөг графикаар хязгаарлагдсан зургийн талбай; b ] функц f (x), Ox тэнхлэг ба x=a ба x= b шулуунууд:

2. Үргэлжилсэн функцуудын график f (x) ба x=a, x= b шугамаар хязгаарлагдсан зургийн талбай:

3. Үргэлжилсэн функцүүдийн графикаар хязгаарлагдсан зургийн талбай f (x) ба:

4. Үргэлжилсэн функцуудын f (x) ба Ox тэнхлэгийн графикаар хязгаарлагдсан зургийн талбай:

"Интеграл. Интеграл ашиглан талбайн тооцоо" сэдвийн бодлого, тест.

• Интеграл

  Хичээл: 4 Даалгавар: 13 Тест: 1

• Интеграл ашиглан талбайг тооцоолох - Эсрэг дериватив ба интеграл 11-р зэрэг

  Хичээл: 1 Даалгавар: 10 Тест: 1

• Эсрэг дериватив - Эсрэг дериватив ба интеграл 11-р зэрэг

  Хичээл: 1 Даалгавар: 11 Тест: 1

• Планиметри: урт ба талбайн тооцоо

  Даалгавар: 7

• Тооцоолол ба хөрвүүлэлт - Математикийн улсын нэгдсэн шалгалтад бэлтгэх Математикийн улсын нэгдсэн шалгалтанд бэлтгэх

  Даалгавар: 10

Өгөгдсөн шугамаар хүрээлэгдсэн дүрсийн талбайг тооцоолж эхлэхээсээ өмнө энэ зургийг координатын системд дүрсэлж үзээрэй. Энэ нь асуудлыг шийдвэрлэхэд илүү хялбар болно.

Энэ сэдвээр онолын материалыг судлах нь эсрэг дериватив ба интеграл гэсэн ойлголтыг эзэмших, тэдгээрийн хоорондын уялдаа холбоог ойлгох, интеграл тооцооллын хамгийн энгийн аргыг эзэмших, функцийн графикаар хязгаарлагдсан тоонуудын талбайг тооцоолоход интегралыг ашиглаж сурах боломжийг олгоно. .

Жишээ.

1. Интегралыг тооцоол

Шийдэл:

Хариулт: 0.

2. Зургаар хязгаарлагдсан зургийн талбайг ол

а) е(x) = 2 X – X 2 ба x тэнхлэг

Шийдэл: f(x) = 2x - x 2 функцийн график нь парабол юм. Орой: (1; 1).

Хариулт:(кв. нэгж).

№___ Огноо________

Сэдэв:Муруй шугаман трапец ба түүний талбай б

Хичээлийн зорилго: Муруй трапец болон түүний талбайг тодорхойлж, муруй трапецын талбайг тооцоолж сур.

ХИЧЭЭЛИЙН ҮЕД

1. Зохион байгуулалтын мөч.

Сурагчидтай мэндлэх, ангийн хичээлд бэлэн байдлыг шалгах, сурагчдын анхаарлыг зохион байгуулах, хичээлийн ерөнхий зорилго, төлөвлөгөөг илчлэх.

2. Гэрийн даалгавар шалгах үе шат.

Зорилго: Бүх сурагчдын гэрийн даалгаврын гүйцэтгэлийн үнэн зөв, бүрэн гүйцэд, ухамсартай байдлыг тогтоох, оюутнуудын мэдлэг, үйл ажиллагааны арга барилын дутагдлыг илрүүлэх. Хүндрэлийн шалтгааныг тодорхойлж, олдсон цоорхойг арилгах.

3. Шинэчлэх үе шат.

Зорилтууд: сургуулийн сурагчдын суралцах сэдлийг хангах, хичээлийн зорилгыг тодорхойлох хамтарсан үйл ажиллагаанд хамруулах. Оюутнуудын субъектив туршлагыг шинэчлэх.

Үндсэн ойлголт, томъёог санацгаая.

Тодорхойлолт.Чиг үүрэг у=е(x), x (а, б),функцийн эсрэг дериватив гэж нэрлэдэг y=f(x), x (а, б),хэрэв хүн бүрт x (а, б)тэгш байдал хадгалагдана

Ф (x)=f(x).

Сэтгэгдэл.Хэрэв е(x)функцийн эсрэг дериватив байдаг f(x), дараа нь ямар ч тогтмол ХАМТ, F(x)+Cнь мөн эсрэг дериватив юм f(x).

Функцийн бүх эсрэг деривативуудыг олох асуудал f(x)интеграл гэж нэрлэдэг ба бүх эсрэг деривативуудын олонлогийг функцийн тодорхойгүй интеграл гэнэ. f(x) By dxболон томилогдсон

Дараах шинж чанарууд явагдана.

1. ;

2. Хэрэв C= Const, тэгвэл
;

3.
.

Сэтгэгдэл.Сургуулийн математикийн хичээлд "тодорхойгүй интеграл" гэсэн нэр томъёог ашигладаггүй бөгөөд үүний оронд "бүх эсрэг деривативуудын багц" гэж хэлдэг.

Энд тодорхойгүй интегралын хүснэгт байна.

Жишээ 1.Функцийн эсрэг деривативыг ол
, цэгээр дамжин өнгөрөх М(2;4).

Шийдэл.Функцийн бүх эсрэг деривативуудын багц
тодорхойгүй интеграл байдаг
. 1 ба 2 интегралын шинж чанарыг ашиглан тооцоолъё. Бидэнд байгаа:

Бүх эсрэг деривативуудын багцыг функцүүдийн гэр бүлээр өгөгдсөн болохыг бид олж мэдсэн y=F(x)+C, тэр бол y=x 3 – 2x+C, Хаана ХАМТ- дурын тогтмол.

Эсрэг дериватив нь цэгээр дамждаг гэдгийг мэдэх М(2;4), түүний координатыг өмнөх илэрхийлэлд орлуулж ол ХАМТ.

4=2 3 –2 2+ХАМТ  ХАМТ=4–8+4; ХАМТ=0.

Хариулт: F(x)=x 3 - 2x- хүссэн антидериватив.

4. Үйл ажиллагааны шинэ үзэл баримтлал, арга барилыг бий болгох.

Зорилго: Оюутнууд судалж буй материалыг хүлээн авах, ойлгох, санах чадварыг баталгаажуулах. Оюутнууд судалж буй материалыг хуулбарлах аргыг эзэмшсэн байх, олж авсан ойлголт, хууль тогтоомж, дүрэм, томъёоны философийн ойлголтыг сурталчлах. Суралцагчдын судалсан материалын үнэн зөв, ухамсартай байдлыг тогтоох, анхан шатны ойлголтын дутагдлыг илрүүлэх, залруулга хийх. Оюутнууд өөрсдийн субьектив туршлагаа шинжлэх ухааны мэдлэгийн шинж тэмдгүүдтэй уялдуулахыг баталгаажуулах.

Онгоцны дүрсүүдийн талбайг олох

Хавтгай дүрсийн талбайг олох асуудал нь эсрэг дериватив (интеграл) олох асуудалтай нягт холбоотой юм. Тухайлбал: функцийн графикаар хязгаарлагдсан муруйн трапецын талбайy=f(x) (f(x)> 0) шулуунx=a; x=b; у= 0 нь функцийн эсрэг деривативын утгуудын зөрүүтэй тэнцүү байнаy=f(x) цэгүүдэдб Тэгээда :

S=F(b)–F(a)

Тодорхой интегралын тодорхойлолтыг өгье.

ТУХАЙ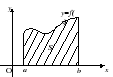
тодорхойлолт.Функцийг зөвшөөр y=f(x)интервал дээр тодорхойлогдсон ба интегралдах [ а,б] орхи F(x)- түүний зарим прототипүүд. Дараа нь тоо F(b)–F(a)-ийн интеграл гэж нэрлэдэг Аөмнө бфункцууд f(x)болон томилогдсон

.

Тэгш байдал
Ньютон-Лейбницийн томьёо гэж нэрлэдэг.

Энэ томьёо нь хавтгай дүрсийн талбайг олох асуудлыг интегралтай холбодог.

Ерөнхийдөө хэрэв зураг нь функцын графикаар хязгаарлагддаг бол y=f(x);y=g(x) (f(x)>g(x)) ба шулуун x=a;x=b, тэгвэл түүний талбай тэнцүү байна:

.

Жишээ 2.Функцийн графикийн аль цэгт y=x 2 + 1 та энэ функцын график болон шулуун шугамаас үүссэн дүрсээс таслахын тулд шүргэгч зурах хэрэгтэй. у= 0, x= 0, x=Хамгийн том талбайтай 1 трапец байна уу?

Шийдэл.Болъё М 0 (х 0 ,y 0 ) – функцийн графикийн цэг y=x 2 + 1, шаардлагатай шүргэгчийг зурсан.

Шүргэдэг тэгшитгэлийг олцгооё y=y 0 +f (х 0 )(x–x 0 ) .

Бидэнд байгаа:

Тийм ч учраас

.

Трапецын талбайг ол OABC.

.

Б– шулуун шугамтай шүргэгч огтлолцох цэг x= 1 

Даалгаврыг функцийн хамгийн том утгыг олох хүртэл багасгасан

С(x)=–x 2 +x+сегмент дээр 1. Бид олох болно С (x)=– 2x+ 1. Нөхцөлөөс эгзэгтэй цэгийг ол С (x)= 0  x=.

Функц нь хамгийн их утгадаа хүрч байгааг бид харж байна x=. Бид олох болно
.

Хариулт:цэг дээр шүргэгчийг зурах ёстой
.

Интегралыг геометрийн утгаар нь олох асуудал байнга тулгардаг гэдгийг анхаарна уу. Энэ асуудал хэрхэн шийдэгдэж байгааг жишээгээр харуулъя.

Жишээ 4.Интегралын геометрийн утгыг ашиглан тооцоол

А )
; б)
.

Шийдэл.

A)
- шугамаар хязгаарлагдсан муруйн трапецын талбайтай тэнцүү.

П хувиргацгаая

– төвтэй тойргийн дээд тал Р(1;0) ба радиус R = 1.

Тийм ч учраас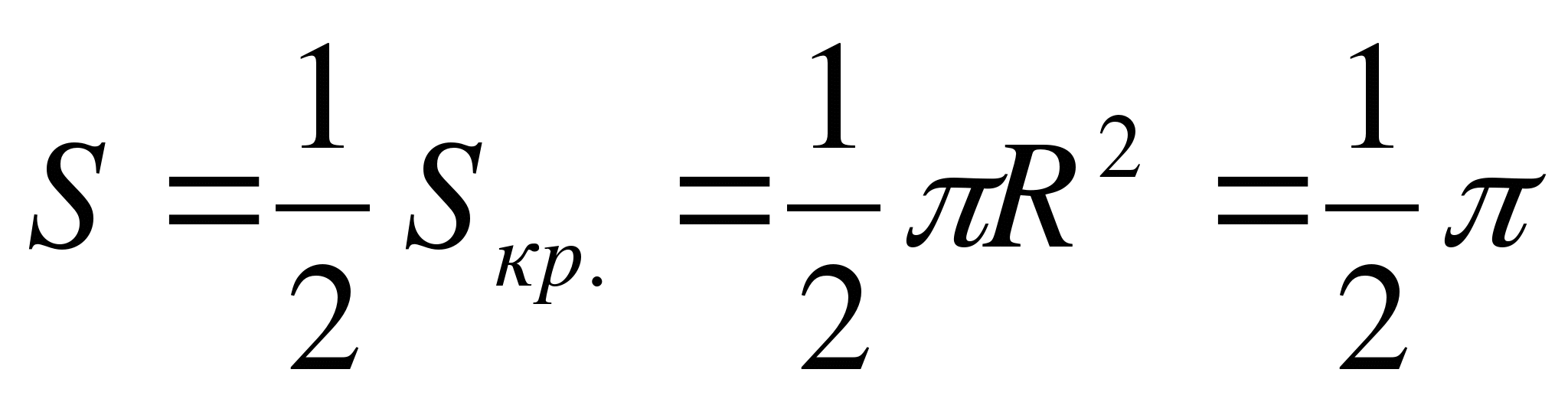
.

Хариулт:
.

b) Үүнтэй адил маргаж, .2 графикаар хязгаарлагдсан талбайг байгуулъя – 2x+ 2, цэгүүдэд шүргэгч А
, Б(4;2)

у=–9x– 59, парабол у= 3x 2 +сүх+ 1, хэрэв энэ нь мэдэгдэж байгаа бол параболын шүргэгч цэг дээр x=– 2 нь тэнхлэгтэй Үхэрөнцгийн хэмжээ arctg 6.

Хай А, хэрэв муруй трапецын талбай нь шугамаар хязгаарлагдах нь мэдэгдэж байгаа бол у= 3x 3 + 2x, x=a, y= 0 нь нэгтэй тэнцүү.

Параболоор хүрээлэгдсэн дүрсийн хамгийн жижиг талбайг ол y=x 2 + 2x– 3 ба шулуун y=kx+ 1.

6.Гэрийн даалгавар мэдээлэл өгөх үе шат.

Зорилго: Оюутнуудад гэрийн даалгавраа гүйцэтгэх зорилго, агуулга, арга зүйг ойлгуулах No18, 19,20,21 сондгой

7. Хичээлийг дүгнэх.

Зорилго: Ангийн болон бие даасан оюутнуудын ажлын чанарын үнэлгээг өгөх.