Kreivės trapecijos samprata. Tema: Kreivinė trapecija ir jos plotas. Naujų koncepcijų ir veikimo metodų formavimas

Figūra, apribota ištisinės neneigiamos funkcijos $f(x)$ atkarpoje $$ ir tiesių $y=0, \ x=a$ ir $x=b$ grafiku, vadinama kreivine trapecija.

Atitinkamos kreivinės trapecijos plotas apskaičiuojamas pagal formulę:

$S=\int\limits_(a)^(b)(f(x)dx).$ (*)

Norėdami rasti kreivinės trapecijos plotą, problemas sąlygiškai padalinsime į $4 $ tipus. Pažvelkime į kiekvieną tipą išsamiau.

I tipas: lenkta trapecija yra aiškiai nurodyta. Tada nedelsdami pritaikykite formulę (*).

Pavyzdžiui, raskite kreivinės trapecijos plotą, kurį riboja funkcijos $y=4-(x-2)^(2)$ grafikas ir linijos $y=0, \ x=1$ ir $x. = 3 USD.

Nubraižykime šią išlenktą trapeciją.

Naudodami formulę (*) randame šios kreivinės trapecijos plotą.

$S=\int\limits_(1)^(3)(\left(4-(x-2)^(2)\right)dx)=\int\limits_(1)^(3)(4dx)- \int\limits_(1)^(3)((x-2)^(2)dx)=4x|_(1)^(3) – \left.\frac((x-2)^(3) )(3)\right|_(1)^(3)=$

$=4(3-1)-\frac(1)(3)\left((3-2)^(3)-(1-2)^(3)\right)=4 \cdot 2 – \frac (1)(3)\kairė((1)^(3)-(-1)^(3)\dešinė) = 8 – \frac(1)(3)(1+1) =$

$=8-\frac(2)(3)=7\frac(1)(3)$ (vnt.$^(2)$).

II tipas: lenkta trapecija nurodoma netiesiogiai.Šiuo atveju tiesės $x=a, \ x=b$ dažniausiai nenurodomos arba nurodomos iš dalies. Tokiu atveju reikia rasti funkcijų $y=f(x)$ ir $y=0$ susikirtimo taškus. Šie taškai bus $a$ ir $b$ taškai.

Pavyzdžiui, raskite figūros plotą, kurį riboja funkcijų $y=1-x^(2)$ ir $y=0$ grafikai.

Raskime susikirtimo taškus. Norėdami tai padaryti, sulyginame dešiniąsias funkcijų puses.

Taigi $a=-1$ ir $b=1$. Nubraižykime šią išlenktą trapeciją.

Raskime šios lenktos trapecijos plotą.

$S=\int\limits_(-1)^(1)(\left(1-x^(2)\right)dx)=\int\limits_(-1)^(1)(1dx)-\int \limits_(-1)^(1)(x^(2)dx)=x|_(-1)^(1) – \left.\frac(x^(3))(3)\right|_ (-1)^(1)=$

$=(1-(-1))-\frac(1)(3)\left(1^(3)-(-1)^(3)\right)=2 – \frac(1)(3) \left(1+1\right) = 2 – \frac(2)(3) = 1\frac(1)(3)$ (vnt.$^(2)$).

III tipas: figūros plotas, apribotas dviejų ištisinių neneigiamų funkcijų susikirtimo.Ši figūra nebus išlenkta trapecija, o tai reiškia, kad negalite apskaičiuoti jos ploto pagal formulę (*). Kaip būti? Pasirodo, šios figūros plotą galima rasti kaip skirtumą tarp kreivių trapecijos plotų, apribotų viršutinės funkcijos ir $y=0$ ($S_(uf)$), ir apatinės funkcijos bei $y. =0$ ($S_(lf)$), kur $x=a, \ x=b$ vaidmenį atlieka šių funkcijų susikirtimo taškų $x$ koordinatės, t.y.

$S=S_(uf)-S_(lf)$. (**)

Skaičiuojant tokias sritis svarbiausia „nepraleisti“ pasirenkant viršutinę ir apatinę funkcijas.

Pavyzdžiui, raskite figūros plotą, kurį riboja funkcijos $y=x^(2)$ ir $y=x+6$.

Raskime šių grafikų susikirtimo taškus:

Pagal Vietos teoremą,

$x_(1)=-2,\x_(2)=3.$

Tai yra $a=-2,\b=3$. Nubraižykime figūrą:

Taigi viršutinė funkcija yra $y=x+6$, o apatinė – $y=x^(2)$. Tada randame $S_(uf)$ ir $S_(lf)$, naudodami formulę (*).

$S_(uf)=\int\limits_(-2)^(3)((x+6)dx)=\int\limits_(-2)^(3)(xdx)+\int\limits_(-2 )^(3)(6dx)=\kairė.\frac(x^(2))(2)\right|_(-2)^(3) + 6x|_(-2)^(3)= 32 .5$ (vnt.$^(2)$).

$S_(lf)=\int\limits_(-2)^(3)(x^(2)dx)=\left.\frac(x^(3))(3)\right|_(-2) ^(3) = \frac(35)(3)$ (vnt.$^(2)$).

Pakeiskime tai, ką radome, į (**) ir gaukime:

$S=32.5-\frac(35)(3)= \frac(125)(6)$ (vnt.$^(2)$).

IV tipas: figūros, apribotos funkcijos (-ų), kuri neatitinka neneigiamumo sąlygos, plotas. Norėdami rasti tokios figūros plotą, turite būti simetriški $Ox$ ašies atžvilgiu ( kitaip tariant, prieš funkcijas įdėkite „minusus“) parodykite plotą ir, naudodami I – III tipuose aprašytus metodus, raskite rodomos srities plotą. Ši sritis bus reikalinga. Pirmiausia gali tekti rasti funkcijų grafikų susikirtimo taškus.

Pavyzdžiui, raskite figūros plotą, kurį riboja funkcijų $y=x^(2)-1$ ir $y=0$ grafikai.

Raskime funkcijų grafikų susikirtimo taškus:

tie. $a=-1$ ir $b=1$. Nubraižykime plotą.

Pavaizduokime sritį simetriškai:

$y=0 \ \Rightarrow \ y=-0=0$

$y=x^(2)-1 \ \Rightrow \ y= -(x^(2)-1) = 1-x^(2)$.

Rezultatas yra kreivinė trapecija, kurią riboja funkcijos $y=1-x^(2)$ ir $y=0$ grafikas. Tai yra problema ieškant antrojo tipo išlenktos trapecijos. Jau išsprendėme. Atsakymas buvo toks: $S= 1\frac(1)(3)$ (vienetai $^(2)$). Tai reiškia, kad reikiamos kreivinės trapecijos plotas yra lygus:

$S=1\frac(1)(3)$ (vnt.$^(2)$).

Išlenktos trapecijos plotas

Kreivinė trapecija yra figūra, apribota grafiku, pateiktu atkarpoje [ a, b] nuolatinė ir neneigiama funkcija f(x), taškais nubrėžtos ordinatės a Ir b, ir ašies segmentas Jautis tarp taškų a Ir b(žr. 2 pav.).

Įrodykime tokį teiginį.

Lenkta trapecija yra kvadratinė figūra, plotas P

Įrodymas. Nuo nuolatinio segmento [ a, b] funkcija yra integruojama, tada bet kuriam teigiamam skaičiui ε galite nurodyti tokį skirsnį T segmentas [ a, b], koks skirtumas S - s < ε , Kur S Ir s- atitinkamai viršutinė ir apatinė skaidinio sumos T. Bet S Ir s yra atitinkamai vienodi S d Ir S i, Kur S d Ir S i- laiptuotų figūrų (daugiakampių) plotai, iš kurių pirmasis yra kreivinėje trapecijoje, o antrasis yra kreivinėje trapecijoje (2 pav. taip pat pavaizduotos šios laiptuotos figūros). Nes S d - S i < ε , tada, remiantis 1 teorema, kreivinė trapecija yra kvadratinė. Kadangi viršutinės ir apatinės sumų Δ → 0 riba yra lygi s ≤ P ≤ S, tada sritis P išlenktą trapeciją galima rasti naudojant (1) formulę.

komentuoti. Jei funkcija f(x) yra tęstinis ir ne teigiamas segmente [ a, b], tada integralo reikšmė lygi kreivinės trapecijos plotui, paimtam su neigiamu ženklu, apribotam funkcijos grafiku f(x), ordinatės taškuose a Ir b ir ašies segmentas Jautis tarp taškų a Ir b. Todėl, jei f(x) pakeičia ženklą, tada jis yra lygus kreivinių trapecijų, esančių aukščiau ir žemiau ašies, paimtos tam tikru ženklu, plotų sumai Jautis, o pirmųjų plotai imami su + ženklu, o antrųjų su - ženklu.

Išlenkto sektoriaus plotas

Tegul kreivė L poliarinėje koordinačių sistemoje pateikiama lygtimi r = r(θ ), α ≤ θ ≤ β (žr. 3 pav.), ir funkcija r(θ ) yra tęstinis ir neneigiamas segmente [ α , β ]. Plokščia figūra, apribota kreive L ir du spinduliai, sudarantys kampus su poliarine ašimi α Ir β , mes paskambinsime kreivinis sektorius.

Įrodykime tokį teiginį. Kreivinis sektorius yra kvadratinė figūra, plotas P kurią galima apskaičiuoti naudojant formulę

Įrodymas. Apsvarstykite skaidinį T segmentas [ α , β ] taškais α = θ 0 < θ 1 < ... < θ n = β ir kiekvienam daliniam segmentui [ θ i -1 , θ i] sudaryti apskritimo sektorius, kurių spindulys lygus mažiausiam r i ir maksimaliai R i vertybes r(θ ) segmente [ θ i -1 , θ i]. Dėl to gauname dvi vėduoklės formos figūras, iš kurių pirmoji yra kreiviniame sektoriuje, o antrojoje – kreivės sektorius (šios vėduoklės formos figūros parodytos 3 pav.). Nurodytų vėduoklės formos figūrų plotai yra lygūs ir atitinkamai. Atkreipkite dėmesį, kad pirmoji iš šių sumų yra mažesnė suma s nurodytos skaidinio funkcijai T segmentas [ α , β ], o antroji suma yra didžiausia suma S tai pačiai funkcijai ir tam pačiam skirsniui. Kadangi funkcija yra integruota į segmentą [ α , β ], tada skirtumas gali būti toks mažas, kiek norisi. Pavyzdžiui, bet kokiam fiksuotam ε > 0 šį skirtumą galima sumažinti ε /2. Dabar į vidinę vėduoklės formos figūrą įbrėžkime daugiakampį K i su plotu S i, kuriam , ir aprašome daugiakampį aplink išorinę vėduoklės formos figūrą K d plotas S d, kuriam * . Akivaizdu, kad pirmasis iš šių daugiakampių yra įbrėžtas į kreivinį sektorių, o antrasis – aplink jį. Kadangi nelygybės yra teisingos

Apibrėžimas. Skirtumas F (b) – F (a) vadinamas funkcijos f (x) integralu intervale [ a ; b ] ir žymimas taip: = F (b) – F (a) – Niutono-Leibnizo formulė.

Geometrinė integralo reikšmė.

Kreivinės trapecijos plotas, apribotas nuolatiniu teigiamu grafiku intervale [a; b ] funkcijos f (x), Ox ašis ir linijos x=a ir x= b:

Plotų skaičiavimas naudojant integralą.

1. Figūros plotas, apribotas ištisiniu neigiamu grafiku intervale [a; b ] funkcijos f (x), Ox ašis ir linijos x=a ir x= b:

2. Figūros plotas, apribotas ištisinių funkcijų f (x) grafikais ir tiesėmis x=a, x= b:

3. Figūros plotas, apribotas ištisinių funkcijų f (x) grafikais ir:

4. Figūros plotas, apribotas ištisinių funkcijų f (x) grafikais ir Ox ašimi:

Uždaviniai ir testai tema "Integralis. Plotų skaičiavimas naudojant integralą"

• Integralinis

  Pamokos: 4 Užduotys: 13 Testai: 1

• Plotų skaičiavimas naudojant integralus - Antiderivative ir integralinis 11 laipsnis

  Pamokos: 1 Užduotys: 10 Testų: 1

• Antidarinis - Antiderivative ir integralinis 11 laipsnis

  Pamokos: 1 Užduotys: 11 Testų: 1

• Planimetrija: ilgių ir plotų skaičiavimas

  Užduotys: 7

• Skaičiavimai ir perskaičiavimai - Pasirengimas vieningam valstybiniam matematikos egzaminui Vieningas valstybinis matematikos egzaminas

  Užduotys: 10

Prieš pradėdami skaičiuoti figūros plotą, kurį riboja nurodytos linijos, pabandykite pavaizduoti šią figūrą koordinačių sistemoje. Tai padės daug lengviau išspręsti problemą.

Teorinės medžiagos šia tema studijavimas suteikia galimybę įsisavinti antidarinės ir integralo sąvokas, suprasti ryšį tarp jų, įsisavinti paprasčiausią integralo skaičiavimo techniką ir išmokti integralą pritaikyti skaičiuojant figūrų plotus, kuriuos riboja funkcijų grafikai. .

Pavyzdžiai.

1. Apskaičiuokite integralą

Sprendimas:

Atsakymas: 0.

2. Raskite figūros plotą, kurį riboja linijos

a) f(x) = 2 X – X 2 ir x ašis

Sprendimas: Funkcijos f(x) = 2x - x 2 grafikas yra parabolė. Viršūnė: (1; 1).

Atsakymas:(kv. vnt.).

Nr.___ Data________

Tema:Kreivinė trapecija ir jos plotas b

Pamokos tikslai: Apibrėžkite lenktą trapeciją ir jos plotą, išmokite apskaičiuoti lenktos trapecijos plotą.

UŽSIĖMIMŲ LAIKOTARPIU

1. Organizacinis momentas.

Mokinių sveikinimas, klasės pasirengimo pamokai tikrinimas, mokinių dėmesio organizavimas, bendrųjų pamokos tikslų ir jos plano atskleidimas.

2. Namų darbų tikrinimo etapas.

Tikslai: Nustatyti visų mokinių namų darbų atlikimo teisingumą, išsamumą ir sąmoningumą, nustatyti mokinių žinių ir veiklos metodų spragas. Nustatykite sunkumų priežastis ir pašalinkite visas rastas spragas.

3. Atnaujinimo etapas.

Tikslai: moksleivių mokymosi motyvacijos užtikrinimas, įtraukimas į bendrą veiklą, siekiant nustatyti pamokos tikslus. Atnaujinkite subjektyvią studentų patirtį.

Prisiminkime pagrindines sąvokas ir formules.

Apibrėžimas. Funkcija y=f(x), x (a, b), vadinamas funkcijos antidariniu y=f(x), x (a, b), jei visiems x (a, b) galioja lygybė

F (x) = f (x).

komentuoti. Jeigu f(x) funkcijai yra antidarinys f(x), tada bet kuriai konstantai SU, F(x)+C taip pat yra antiderivatinis vaistas f(x).

Visų funkcijos antidarinių suradimo problema f(x) vadinama integracija, o visų antidarinių aibė – neapibrėžtuoju funkcijos integralu f(x) Autorius dx ir yra paskirtas

Atsiranda šios savybės:

1 . ;

2. Jeigu C= Tada Const
;

3 .
.

komentuoti. Mokykliniuose matematikos kursuose terminas „neapibrėžtas integralas“ nevartojamas, vietoj to sakoma „visų antiderivatų rinkinys“.

Čia yra neapibrėžtų integralų lentelė.

1 pavyzdys. Raskite funkcijos antidarinį
, einantis per tašką M(2;4).

Sprendimas. Visų funkcijos antidarinių rinkinys
yra neapibrėžtas integralas
. Apskaičiuokime jį naudodami integralo 1 ir 2 savybes. Mes turime:

Mes nustatėme, kad visų antidarinių rinkinį suteikia funkcijų šeima y=F(x)+C, tai yra y=x 3 – 2x+C, Kur SU– savavališka konstanta.

Žinant, kad antidarinys eina per tašką M(2;4), pakeiskite jo koordinates į ankstesnę išraišką ir suraskite SU.

4=2 3 –2 2+SU  SU=4–8+4; SU=0.

Atsakymas: F(x)=x 3 - 2x- norimą antidarinį.

4. Naujų koncepcijų ir veiksmų metodų formavimas.

Tikslai: Užtikrinti, kad mokiniai suvoktų, suprastų ir įsimintų studijuojamą medžiagą. Užtikrinti, kad mokiniai įsisavintų studijuojamos medžiagos atkūrimo būdus, skatintų filosofinį įsisavinamų sąvokų, dėsnių, taisyklių, formulių supratimą. Nustatyti studentų studijuojamos medžiagos teisingumą ir supratimą, nustatyti pirminio supratimo spragas ir atlikti pataisymus. Įsitikinkite, kad studentai savo subjektyvią patirtį susieja su mokslo žinių ženklais.

Plokštumos figūrų plotų radimas

Plokštumos figūros ploto radimo problema yra glaudžiai susijusi su antidarinių (integracijos) paieškos problema. Būtent: kreivinės trapecijos plotas, kurį riboja funkcijos grafikasy=f(x) (f(x)> 0) tiesusx=a; x=b; y= 0, lygus skirtumui tarp funkcijos antidarinės verčiųy=f(x) taškuoseb Ira :

S=F(b)–F(a)

Pateiksime apibrėžtojo integralo apibrėžimą.

APIE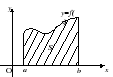
apibrėžimas. Tegul funkcija y=f(x) apibrėžtas ir integruojamas intervale [ a, b] Paleisk F(x)- kai kurie jo prototipai. Tada skaičius F(b)–F(a) vadinamas integralu A prieš b funkcijas f(x) ir yra paskirtas

.

Lygybė
vadinama Niutono-Leibnizo formule.

Ši formulė sujungia plokštumos figūros ploto radimo problemą su integralu.

Apskritai, jei figūrą riboja funkcijų grafikai y=f(x);y=g(x) (f(x)>g(x)) ir tiesiai x=a;x=b, tada jo plotas lygus:

.

2 pavyzdys. Kuriame funkcijos grafiko taške y=x 2 + 1 reikia nubrėžti liestinę, kad ji nukirstų nuo figūros, sudarytos iš šios funkcijos grafiko ir tiesių linijų y= 0, x= 0, x= 1 trapecija, kurios plotas didžiausias?

Sprendimas. Leisti M 0 (x 0 ,y 0 ) – funkcijos grafiko taškas y=x 2 + 1, kuriame nubrėžta reikiama liestinė.

Raskime liestinės lygtį y=y 0 +f (x 0 )(x–x 0 ) .

Mes turime:

Štai kodėl

.

Raskite trapecijos plotą OABC.

.

B– liestinės ir tiesės susikirtimo taškas x= 1 

Užduotis buvo sumažinta iki didžiausios funkcijos reikšmės radimo

S(x)=–x 2 +x+ 1 segmente. Mes rasime S (x)=– 2x+ 1. Raskite kritinį tašką iš būklės S (x)= 0  x=.

Matome, kad funkcija pasiekia didžiausią vertę x=. Mes rasime
.

Atsakymas: taške turi būti nubrėžta liestinė
.

Atkreipkite dėmesį, kad dažnai susiduriama su integralo radimo pagal jo geometrinę reikšmę problema. Parodykime pavyzdžiu, kaip ši problema išspręsta.

4 pavyzdys. Naudodamiesi integralo geometrine reikšme, apskaičiuokite

A )
; b)
.

Sprendimas.

A)
– lygus kreivinės trapecijos, apribotos linijomis, plotui.

P transformuokime

– viršutinė apskritimo pusė su centru R(1;0) ir spindulys R= 1.

Štai kodėl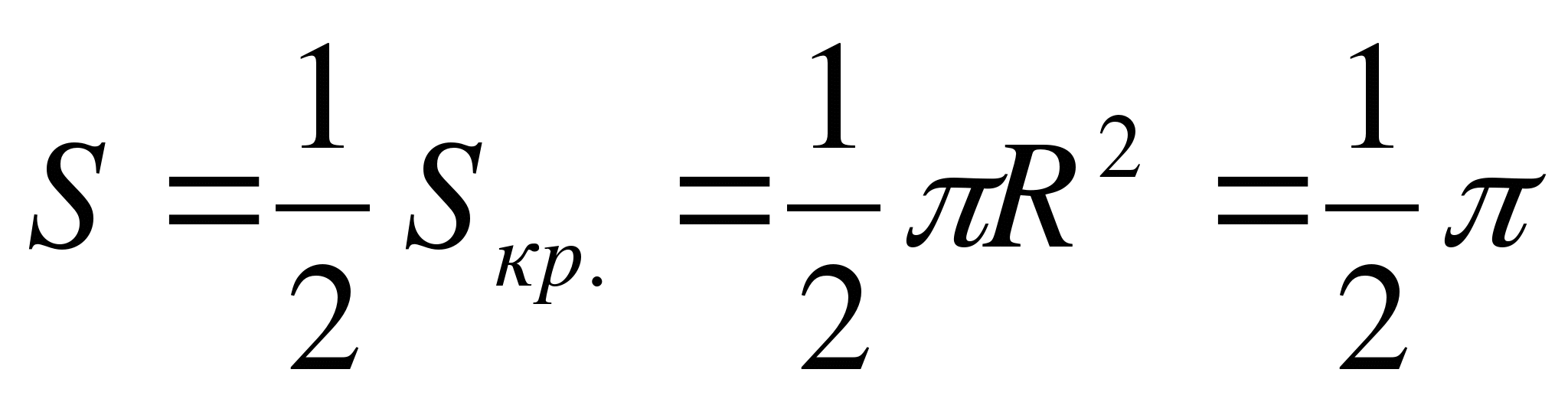
.

Atsakymas:
.

b) Argumentuodami panašiai, sukurkime plotą, apribotą grafikais .2 – 2x+ 2, jo liestinė taškuose A
, B(4;2)

y=–9x- 59, parabolė y= 3x 2 +kirvis+ 1, jei žinoma, kad parabolės liestinė taške x=– 2 yra su ašimi Jautis kampo dydis arctg 6.

Rasti A, jei žinoma, kad kreivinės trapecijos, apribotos linijomis, plotas y= 3x 3 + 2x, x=a, y= 0 yra lygus vienetui.

Raskite mažiausią figūros plotą, kurį riboja parabolė y=x 2 + 2x- 3 ir tiesiai y=kx+ 1.

6.Namų darbų informacijos etapas.

Tikslai: Užtikrinti, kad mokiniai suprastų namų darbų paskirtį, turinį ir atlikimo būdus Nr.18, 19,20,21 nelyginis

7. Pamokos apibendrinimas.

Tikslas: Kokybiškai įvertinti klasės ir atskirų mokinių darbą.