The concept of a curved trapezoid. Topic: Curvilinear trapezoid and its area. Formation of new concepts and methods of action

A figure bounded by the graph of a continuous non-negative function $f(x)$ on the segment $$ and the lines $y=0, \ x=a$ and $x=b$ is called a curvilinear trapezoid.

The area of ​​the corresponding curvilinear trapezoid is calculated by the formula:

$S=\int\limits_(a)^(b)(f(x)dx).$ (*)

We will conditionally divide problems to find the area of ​​a curvilinear trapezoid into $4$ types. Let's look at each type in more detail.

Type I: a curved trapezoid is specified explicitly. Then immediately apply the formula (*).

For example, find the area of ​​a curvilinear trapezoid bounded by the graph of the function $y=4-(x-2)^(2)$ and the lines $y=0, \ x=1$ and $x=3$.

Let's draw this curved trapezoid.

Using formula (*), we find the area of ​​this curvilinear trapezoid.

$S=\int\limits_(1)^(3)(\left(4-(x-2)^(2)\right)dx)=\int\limits_(1)^(3)(4dx)- \int\limits_(1)^(3)((x-2)^(2)dx)=4x|_(1)^(3) – \left.\frac((x-2)^(3) )(3)\right|_(1)^(3)=$

$=4(3-1)-\frac(1)(3)\left((3-2)^(3)-(1-2)^(3)\right)=4 \cdot 2 – \frac (1)(3)\left((1)^(3)-(-1)^(3)\right) = 8 – \frac(1)(3)(1+1) =$

$=8-\frac(2)(3)=7\frac(1)(3)$ (units$^(2)$).

Type II: the curved trapezoid is specified implicitly. In this case, the straight lines $x=a, \ x=b$ are usually not specified or partially specified. In this case, you need to find the intersection points of the functions $y=f(x)$ and $y=0$. These points will be points $a$ and $b$.

For example, find the area of ​​a figure bounded by the graphs of the functions $y=1-x^(2)$ and $y=0$.

Let's find the intersection points. To do this, we equate the right-hand sides of the functions.

Thus, $a=-1$ and $b=1$. Let's draw this curved trapezoid.

Let's find the area of ​​this curved trapezoid.

$S=\int\limits_(-1)^(1)(\left(1-x^(2)\right)dx)=\int\limits_(-1)^(1)(1dx)-\int \limits_(-1)^(1)(x^(2)dx)=x|_(-1)^(1) – \left.\frac(x^(3))(3)\right|_ (-1)^(1)=$

$=(1-(-1))-\frac(1)(3)\left(1^(3)-(-1)^(3)\right)=2 – \frac(1)(3) \left(1+1\right) = 2 – \frac(2)(3) = 1\frac(1)(3)$ (units$^(2)$).

Type III: the area of ​​a figure limited by the intersection of two continuous non-negative functions. This figure will not be a curved trapezoid, which means you cannot calculate its area using formula (*). How to be? It turns out that the area of ​​this figure can be found as the difference between the areas of curvilinear trapezoids bounded by the upper function and $y=0$ ($S_(uf)$), and the lower function and $y=0$ ($S_(lf)$), where the role of $x=a, \ x=b$ is played by the $x$ coordinates of the points of intersection of these functions, i.e.

$S=S_(uf)-S_(lf)$. (**)

The most important thing when calculating such areas is not to “miss” with the choice of the upper and lower functions.

For example, find the area of ​​a figure bounded by the functions $y=x^(2)$ and $y=x+6$.

Let's find the intersection points of these graphs:

According to Vieta's theorem,

$x_(1)=-2,\ x_(2)=3.$

That is, $a=-2,\b=3$. Let's draw a figure:

Thus, the top function is $y=x+6$, and the bottom function is $y=x^(2)$. Next, we find $S_(uf)$ and $S_(lf)$ using formula (*).

$S_(uf)=\int\limits_(-2)^(3)((x+6)dx)=\int\limits_(-2)^(3)(xdx)+\int\limits_(-2 )^(3)(6dx)=\left.\frac(x^(2))(2)\right|_(-2)^(3) + 6x|_(-2)^(3)= 32 .5$ (units$^(2)$).

$S_(lf)=\int\limits_(-2)^(3)(x^(2)dx)=\left.\frac(x^(3))(3)\right|_(-2) ^(3) = \frac(35)(3)$ (units$^(2)$).

Let's substitute what we found into (**) and get:

$S=32.5-\frac(35)(3)= \frac(125)(6)$ (units$^(2)$).

Type IV: the area of ​​a figure bounded by a function(s) that does not satisfy the non-negativity condition. In order to find the area of ​​such a figure, you need to be symmetrical about the $Ox$ axis ( in other words, put “minuses” in front of the functions) display the area and, using the methods outlined in types I – III, find the area of ​​the displayed area. This area will be the required area. First, you may have to find the intersection points of the function graphs.

For example, find the area of ​​a figure bounded by the graphs of the functions $y=x^(2)-1$ and $y=0$.

Let's find the intersection points of the function graphs:

those. $a=-1$, and $b=1$. Let's draw the area.

Let's display the area symmetrically:

$y=0 \ \Rightarrow \ y=-0=0$

$y=x^(2)-1 \ \Rightarrow \ y= -(x^(2)-1) = 1-x^(2)$.

The result is a curvilinear trapezoid bounded by the graph of the function $y=1-x^(2)$ and $y=0$. This is a problem to find a curved trapezoid of the second type. We have already solved it. The answer was: $S= 1\frac(1)(3)$ (units $^(2)$). This means that the area of ​​the required curvilinear trapezoid is equal to:

$S=1\frac(1)(3)$ (units$^(2)$).

Area of ​​a curved trapezoid

Curvilinear trapezoid is a figure bounded by a graph given on the segment [ a, b] continuous and non-negative function f(x), ordinates drawn at points a And b, and axis segment Ox between points a And b(see Fig. 2).

Let us prove the following statement.

A curved trapezoid is a squared figure, area P

Proof. Since continuous on the segment [ a, b] the function is integrable, then for any positive number ε you can specify such a partition T segment [ a, b], what is the difference S - s < ε , Where S And s- the upper and lower sums of the partition, respectively T. But S And s are equal respectively S d And S i, Where S d And S i- areas of stepped figures (polygons), the first of which contains a curvilinear trapezoid, and the second is contained in a curvilinear trapezoid (Fig. 2 also shows these stepped figures). Because S d - S i < ε , then, by virtue of Theorem 1, the curvilinear trapezoid is squarable. Since the limit for Δ → 0 of the upper and lower sums is equal to s ≤ P ≤ S, then the area P curved trapezoid can be found using formula (1).

Comment. If the function f(x) is continuous and non-positive on the segment [ a, b], then the value of the integral is equal to the area of ​​the curvilinear trapezoid taken with a negative sign, limited by the graph of the function f(x), ordinates at points a And b and axis segment Ox between points a And b. Therefore, if f(x) changes sign, then it is equal to the sum of the areas of curvilinear trapezoids located above and below the axis taken with a certain sign Ox, and the areas of the former are taken with the + sign, and of the latter with the - sign.

Area of ​​a curved sector

Let the curve L is given in the polar coordinate system by the equation r = r(θ ), α ≤ θ ≤ β (see Fig. 3), and the function r(θ ) is continuous and non-negative on the segment [ α , β ]. A flat figure bounded by a curve L and two rays making angles with the polar axis α And β , we will call curvilinear sector.

Let us prove the following statement. A curvilinear sector is a squared figure, area P which can be calculated using the formula

Proof. Consider the partition T segment [ α , β ] dots α = θ 0 < θ 1 < ... < θ n = β and for each partial segment [ θ i -1 , θ i] construct circular sectors whose radii are equal to the minimum r i and maximum R i values r(θ ) on the segment [ θ i -1 , θ i]. As a result, we obtain two fan-shaped figures, the first of which is contained in the curvilinear sector, and the second contains the curvilinear sector (these fan-shaped figures are shown in Fig. 3). The areas of and of the indicated fan-shaped figures are equal to and respectively. Note that the first of these sums is the lower sum s for a function for a specified partition T segment [ α , β ], and the second sum is the top sum S for the same function and the same partition. Since the function is integrable on the segment [ α , β ], then the difference can be as small as desired. For example, for any fixed ε > 0 this difference can be made smaller ε /2. Let us now inscribe a polygon into the inner fan-shaped figure Q i with area S i, for which , and we describe a polygon around the external fan-shaped figure Q d area S d, for which * . Obviously, the first of these polygons is inscribed in a curvilinear sector, and the second is circumscribed around it. Since the inequalities are true

Definition. The difference F (b) – F (a) is called the integral of the function f (x) on the interval [ a ; b ] and is denoted as follows: = F (b) – F (a) – Newton-Leibniz formula.

Geometric meaning of the integral.

The area of ​​a curvilinear trapezoid bounded by a continuous positive graph on the interval [a; b ] functions f (x), the Ox axis and the lines x=a and x= b:

Calculating areas using an integral.

1.The area of ​​a figure limited by a continuous negative graph on the interval [a; b ] functions f (x), the Ox axis and the lines x=a and x= b:

2. The area of ​​the figure limited by the graphs of continuous functions f (x) and the lines x=a, x= b:

3. The area of ​​the figure limited by the graphs of continuous functions f (x) and:

4. The area of ​​the figure limited by the graphs of continuous functions f (x) and the Ox axis:

Problems and tests on the topic "Integral. Calculation of areas using the integral"

• Integral

  Lessons: 4 Assignments: 13 Tests: 1

• Calculating areas using integrals - Antiderivative and integral grade 11

  Lessons: 1 Assignments: 10 Tests: 1

• Antiderivative - Antiderivative and integral grade 11

  Lessons: 1 Assignments: 11 Tests: 1

• Planimetry: calculation of lengths and areas

  Tasks: 7

• Calculations and Conversions - Preparation for the Unified State Examination in Mathematics Unified State Examination in Mathematics

  Tasks: 10

Before you start calculating the area of ​​a figure bounded by given lines, try to depict this figure in a coordinate system. This will make solving the problem much easier.

Studying theoretical materials on this topic gives you the opportunity to master the concepts of antiderivative and integral, understand the connection between them, master the simplest technique of integral calculus, and learn to apply the integral to calculating the areas of figures limited by graphs of functions.

Examples.

1. Calculate the integral

Solution:

Answer: 0.

2. Find the area of ​​the figure bounded by the lines

a) f(x) = 2 X – X 2 and x-axis

Solution: The graph of the function f(x) = 2x - x 2 is a parabola. Vertex: (1; 1).

Answer:(sq. units).

No.___ Date________

Subject:Curvilinear trapezoid and its area b

Lesson Objectives: Define a curved trapezoid and its area, learn to calculate the area of ​​a curved trapezoid.

DURING THE CLASSES

1. Organizational moment.

Greeting students, checking the class's readiness for the lesson, organizing students' attention, revealing the general goals of the lesson and its plan.

2. Homework checking stage.

Objectives: To establish the correctness, completeness and awareness of the performance of homework by all students, to identify gaps in students’ knowledge and methods of activity. Determine the causes of difficulties and eliminate any gaps found.

3. Update stage.

Objectives: ensuring the motivation of schoolchildren’s learning, inclusion in joint activities to determine the goals of the lesson. Update the subjective experience of students.

Let's remember the basic concepts and formulas.

Definition. Function y=f(x), x (a,b), is called the antiderivative of the function y=f(x), x (a,b), if for everyone x (a,b) equality holds

F (x)=f(x).

Comment. If f(x) there is an antiderivative for the function f(x), then for any constant WITH, F(x)+C is also an antiderivative for f(x).

The problem of finding all antiderivatives of a function f(x) is called integration, and the set of all antiderivatives is called the indefinite integral for the function f(x) By dx and is designated

The following properties take place:

1 . ;

2 . If C= Const, then
;

3 .
.

Comment. In school mathematics courses, the term “indefinite integral” is not used; instead, they say “the set of all antiderivatives.”

Here is a table of indefinite integrals.

Example 1. Find an antiderivative for a function
, passing through the point M(2;4).

Solution. The set of all antiderivatives of a function
there is an indefinite integral
. Let's calculate it using the properties of the integral 1 and 2. We have:

We found that the set of all antiderivatives is given by a family of functions y=F(x)+C, that is y=x 3 – 2x+C, Where WITH– arbitrary constant.

Knowing that the antiderivative passes through the point M(2;4), substitute its coordinates into the previous expression and find WITH.

4=2 3 –2 2+WITH  WITH=4–8+4; WITH=0.

Answer: F(x)=x 3 - 2x- the desired antiderivative.

4. Formation of new concepts and methods of action.

Objectives: To ensure that students perceive, comprehend and remember the material being studied. Ensure that students master the methods of reproducing the studied material, promote philosophical understanding of the concepts, laws, rules, and formulas being acquired. To establish the correctness and awareness of the studied material by students, to identify gaps in primary understanding, and to carry out corrections. Ensure that students correlate their subjective experience with signs of scientific knowledge.

Finding the areas of plane figures

The problem of finding the area of ​​a plane figure is closely related to the problem of finding antiderivatives (integration). Namely: the area of ​​a curvilinear trapezoid limited by the graph of a functiony=f(x) (f(x)> 0) straightx=a; x=b; y= 0, equal to the difference between the values ​​of the antiderivative for the functiony=f(x) at pointsb Anda :

S=F(b)–F(a)

Let us give the definition of a definite integral.

ABOUT
definition. Let the function y=f(x) defined and integrable on the interval [ a,b] let it go F(x)- some of its prototypes. Then the number F(b)–F(a) called the integral of A before b functions f(x) and is designated

.

Equality
called the Newton–Leibniz formula.

This formula connects the problem of finding the area of ​​a plane figure with an integral.

In general, if the figure is limited by function graphs y=f(x);y=g(x) (f(x)>g(x)) and straight x=a;x=b, then its area is equal to:

.

Example 2. At what point in the graph of the function y=x 2 + 1 you need to draw a tangent so that it cuts off from the figure formed by the graph of this function and straight lines y= 0, x= 0, x= 1 trapezoid with the largest area?

Solution. Let M 0 (x 0 ,y 0 ) – point of the function graph y=x 2 + 1, in which the required tangent is drawn.

Let's find the tangent equation y=y 0 +f (x 0 )(x–x 0 ) .

We have:

That's why

.

Find the area of ​​the trapezoid OABC.

.

B– point of intersection of the tangent with the straight line x= 1 

The task was reduced to finding the largest value of the function

S(x)=–x 2 +x+ 1 on the segment. We'll find S (x)=– 2x+ 1. Find the critical point from the condition S (x)= 0  x=.

We see that the function reaches its greatest value at x=. We'll find
.

Answer: the tangent must be drawn at the point
.

Note that the problem of finding an integral based on its geometric meaning is often encountered. Let us show with an example how this problem is solved.

Example 4. Using the geometric meaning of the integral, calculate

A )
; b)
.

Solution.

A)
– equal to the area of ​​a curvilinear trapezoid bounded by lines.

P let's transform

– the upper half of the circle with the center R(1;0) and radius R= 1.

That's why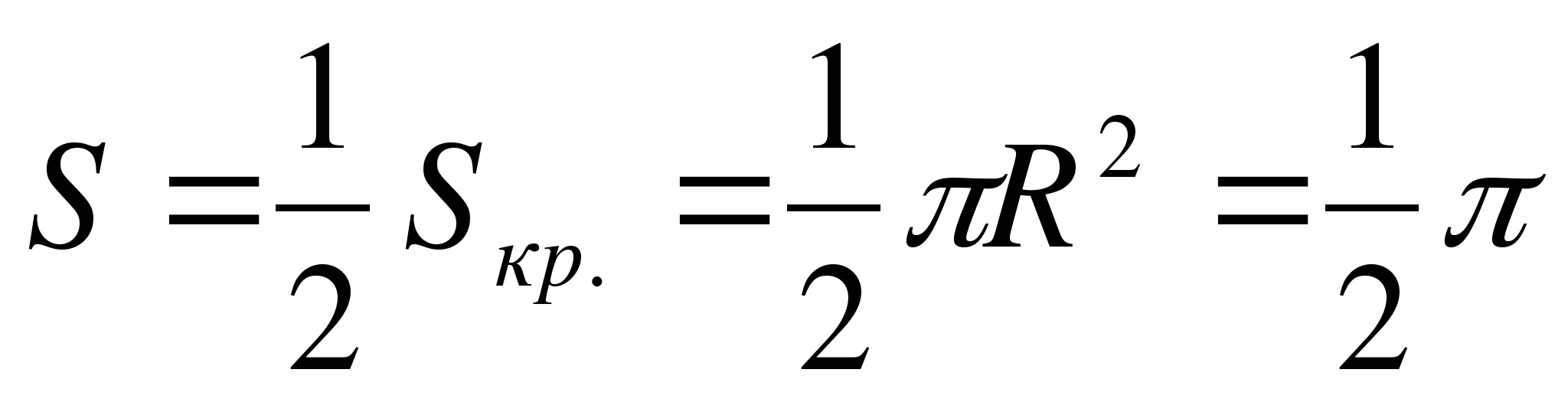
.

Answer:
.

b) Arguing similarly, let’s construct an area limited by graphs .2 – 2x+ 2, tangent to it at points A
, B(4;2)

y=–9x– 59, parabola y= 3x 2 +ax+ 1, if it is known that the tangent to the parabola at the point x=– 2 is with axis Ox angle size arctg 6.

Find A, if it is known that the area of ​​a curvilinear trapezoid bounded by lines y= 3x 3 + 2x, x=a, y= 0 is equal to one.

Find the smallest area of ​​a figure bounded by a parabola y=x 2 + 2x– 3 and straight y=kx+ 1.

6.Homework information stage.

Objectives: To ensure that students understand the purpose, content and methods of completing homework. No. 18, 19,20,21 odd

7. Summing up the lesson.

Objective: To provide a qualitative assessment of the work of the class and individual students.