வளைந்த ட்ரேப்சாய்டின் கருத்து. தலைப்பு: கர்விலினியர் ட்ரேப்சாய்டு மற்றும் அதன் பகுதி. புதிய கருத்துக்கள் மற்றும் செயல் முறைகளின் உருவாக்கம்

$$ பிரிவின் $f(x)$ மற்றும் $y=0, \ x=a$ மற்றும் $x=b$ ஆகிய கோடுகளின் தொடர்ச்சியான எதிர்மறை அல்லாத செயல்பாட்டின் வரைபடத்தால் வரையறுக்கப்பட்ட ஒரு உருவம் வளைவு ட்ரேப்சாய்டு எனப்படும்.

தொடர்புடைய வளைவு ட்ரேப்சாய்டின் பரப்பளவு சூத்திரத்தால் கணக்கிடப்படுகிறது:

$S=\int\limits_(a)^(b)(f(x)dx).$ (*)

வளைந்த ட்ரேப்சாய்டின் பகுதியை $4$ வகைகளாகக் கண்டறிவதற்கான சிக்கல்களை நிபந்தனையுடன் பிரிப்போம். ஒவ்வொரு வகையையும் இன்னும் விரிவாகப் பார்ப்போம்.

வகை I: வளைந்த ட்ரேப்சாய்டு வெளிப்படையாகக் குறிப்பிடப்படுகிறது.பின்னர் உடனடியாக சூத்திரத்தைப் பயன்படுத்தவும் (*).

எடுத்துக்காட்டாக, $y=4-(x-2)^(2)$ செயல்பாட்டின் வரைபடம் மற்றும் $y=0, \ x=1$ மற்றும் $x ஆகிய கோடுகளால் எல்லைப்படுத்தப்பட்ட வளைந்த ட்ரேப்சாய்டின் பகுதியைக் கண்டறியவும். =3$.

இந்த வளைந்த ட்ரேப்சாய்டை வரைவோம்.

சூத்திரத்தைப் பயன்படுத்தி (*), இந்த வளைவு ட்ரேப்சாய்டின் பகுதியைக் காண்கிறோம்.

$S=\int\limits_(1)^(3)(\left(4-(x-2)^(2)\right)dx)=\int\limits_(1)^(3)(4dx)- \int\limits_(1)^(3)((x-2)^(2)dx)=4x|_(1)^(3) – \left.\frac((x-2)^(3) )(3)\வலது|_(1)^(3)=$

$=4(3-1)-\frac(1)(3)\இடது((3-2)^(3)-(1-2)^(3)\வலது)=4 \cdot 2 – \frac (1)(3)\இடது((1)^(3)-(-1)^(3)\வலது) = 8 – \frac(1)(3)(1+1) =$

$=8-\frac(2)(3)=7\frac(1)(3)$ (அலகுகள்$^(2)$).

வகை II: வளைந்த ட்ரேப்சாய்டு மறைமுகமாக குறிப்பிடப்படுகிறது.இந்த வழக்கில், நேர்கோடுகள் $x=a, \ x=b$ பொதுவாக குறிப்பிடப்படவில்லை அல்லது பகுதியளவில் குறிப்பிடப்படவில்லை. இந்த வழக்கில், $y=f(x)$ மற்றும் $y=0$ செயல்பாடுகளின் குறுக்குவெட்டு புள்ளிகளை நீங்கள் கண்டுபிடிக்க வேண்டும். இந்த புள்ளிகள் $a$ மற்றும் $b$ புள்ளிகளாக இருக்கும்.

எடுத்துக்காட்டாக, $y=1-x^(2)$ மற்றும் $y=0$ ஆகிய சார்புகளின் வரைபடங்களால் வரையறுக்கப்பட்ட ஒரு உருவத்தின் பகுதியைக் கண்டறியவும்.

குறுக்குவெட்டு புள்ளிகளைக் கண்டுபிடிப்போம். இதைச் செய்ய, செயல்பாடுகளின் வலது பக்கங்களை சமன் செய்கிறோம்.

எனவே, $a=-1$ மற்றும் $b=1$. இந்த வளைந்த ட்ரேப்சாய்டை வரைவோம்.

இந்த வளைந்த ட்ரேப்சாய்டின் பகுதியைக் கண்டுபிடிப்போம்.

$S=\int\limits_(-1)^(1)(\left(1-x^(2)\right)dx)=\int\limits_(-1)^(1)(1dx)-\int \limits_(-1)^(1)(x^(2)dx)=x|_(-1)^(1) – \இடது.\frac(x^(3))(3)\வலது|_ (-1)^(1)=$

$=(1-(-1))-\frac(1)(3)\இடது(1^(3)-(-1)^(3)\வலது)=2 – \frac(1)(3) \இடது(1+1\வலது) = 2 – \frac(2)(3) = 1\frac(1)(3)$ (அலகுகள்$^(2)$).

வகை III: இரண்டு தொடர்ச்சியான எதிர்மறையான செயல்பாடுகளின் குறுக்குவெட்டு மூலம் வரையறுக்கப்பட்ட உருவத்தின் பரப்பளவு.இந்த எண்ணிக்கை ஒரு வளைந்த ட்ரெப்சாய்டாக இருக்காது, அதாவது சூத்திரத்தை (*) பயன்படுத்தி அதன் பகுதியை கணக்கிட முடியாது. எப்படி இருக்க வேண்டும்?இந்த உருவத்தின் பரப்பளவு மேல் செயல்பாடு மற்றும் $y=0$ ($S_(uf)$) மற்றும் கீழ் செயல்பாடு மற்றும் $y ஆகியவற்றால் கட்டுப்படுத்தப்பட்ட வளைவு ட்ரெப்சாய்டுகளின் பகுதிகளுக்கு இடையே உள்ள வேறுபாட்டைக் காணலாம். =0$ ($S_(lf)$), இதில் $x=a, \ x=b$ பங்கு இந்த செயல்பாடுகளின் குறுக்குவெட்டு புள்ளிகளின் $x$ ஆயத்தொலைவுகளால் விளையாடப்படுகிறது, அதாவது.

$S=S_(uf)-S_(lf)$. (**)

அத்தகைய பகுதிகளை கணக்கிடும் போது மிக முக்கியமான விஷயம், மேல் மற்றும் கீழ் செயல்பாடுகளின் தேர்வுடன் "மிஸ்" செய்யக்கூடாது.

எடுத்துக்காட்டாக, $y=x^(2)$ மற்றும் $y=x+6$ ஆகிய செயல்பாடுகளால் வரையறுக்கப்பட்ட உருவத்தின் பகுதியைக் கண்டறியவும்.

இந்த வரைபடங்களின் குறுக்குவெட்டு புள்ளிகளைக் கண்டுபிடிப்போம்:

வியட்டாவின் தேற்றத்தின்படி,

$x_(1)=-2,\ x_(2)=3.$

அதாவது, $a=-2,\b=3$. ஒரு உருவத்தை வரைவோம்:

எனவே, மேல் செயல்பாடு $y=x+6$, மற்றும் கீழ் செயல்பாடு $y=x^(2)$. அடுத்து, சூத்திரம் (*) ஐப் பயன்படுத்தி $S_(uf)$ மற்றும் $S_(lf)$ ஆகியவற்றைக் காண்கிறோம்.

$S_(uf)=\int\limits_(-2)^(3)((x+6)dx)=\int\limits_(-2)^(3)(xdx)+\int\limits_(-2 )^(3)(6dx)=\இடது.\frac(x^(2))(2)\வலது|_(-2)^(3) + 6x|_(-2)^(3)= 32 .5$ (அலகுகள்$^(2)$).

$S_(lf)=\int\limits_(-2)^(3)(x^(2)dx)=\இடது.\frac(x^(3))(3)\வலது|_(-2) ^(3) = \frac(35)(3)$ (அலகுகள்$^(2)$).

நாம் கண்டுபிடித்ததை (**) மாற்றுவோம்:

$S=32.5-\frac(35)(3)= \frac(125)(6)$ (அலகுகள்$^(2)$).

வகை IV: எதிர்மறை அல்லாத நிலையைத் திருப்திப்படுத்தாத ஒரு செயல்பாடு(கள்) மூலம் வரையறுக்கப்பட்ட உருவத்தின் பரப்பளவு.அத்தகைய உருவத்தின் பரப்பளவைக் கண்டறிய, நீங்கள் $Ox$ அச்சில் சமச்சீராக இருக்க வேண்டும் ( வேறு வார்த்தைகளில் கூறுவதானால்,செயல்பாடுகளுக்கு முன்னால் "மைனஸ்கள்" வைக்கவும்) பகுதியைக் காட்டவும், I - III வகைகளில் கோடிட்டுக் காட்டப்பட்டுள்ள முறைகளைப் பயன்படுத்தி, காட்டப்படும் பகுதியின் பகுதியைக் கண்டறியவும். இந்த பகுதி தேவையான பகுதியாக இருக்கும். முதலில், நீங்கள் செயல்பாட்டு வரைபடங்களின் குறுக்குவெட்டு புள்ளிகளைக் கண்டறிய வேண்டும்.

எடுத்துக்காட்டாக, $y=x^(2)-1$ மற்றும் $y=0$ ஆகிய சார்புகளின் வரைபடங்களால் வரையறுக்கப்பட்ட ஒரு உருவத்தின் பகுதியைக் கண்டறியவும்.

செயல்பாட்டு வரைபடங்களின் குறுக்குவெட்டு புள்ளிகளைக் கண்டுபிடிப்போம்:

அந்த. $a=-1$, மற்றும் $b=1$. பகுதியை வரைவோம்.

பகுதியை சமச்சீராகக் காண்பிப்போம்:

$y=0 \ \Rightarrow \ y=-0=0$

$y=x^(2)-1 \\Rightarrow \ y= -(x^(2)-1) = 1-x^(2)$.

இதன் விளைவாக $y=1-x^(2)$ மற்றும் $y=0$ செயல்பாட்டின் வரைபடத்தால் கட்டுப்படுத்தப்பட்ட ஒரு வளைவு ட்ரேப்சாய்டு ஆகும். இரண்டாவது வகையின் வளைந்த ட்ரேப்சாய்டைக் கண்டுபிடிப்பதில் இது ஒரு சிக்கல். நாங்கள் ஏற்கனவே அதை தீர்த்துவிட்டோம். பதில்: $S= 1\frac(1)(3)$ (அலகுகள் $^(2)$). இதன் பொருள் தேவையான வளைவு ட்ரேப்சாய்டின் பரப்பளவு இதற்கு சமம்:

$S=1\frac(1)(3)$ (அலகுகள்$^(2)$).

வளைந்த ட்ரேப்சாய்டின் பகுதி

வளைவு ட்ரேப்சாய்டுபிரிவில் கொடுக்கப்பட்ட வரைபடத்தால் வரையறுக்கப்பட்ட ஒரு உருவம் [ அ, பி] தொடர்ச்சியான மற்றும் எதிர்மறை அல்லாத செயல்பாடு f(எக்ஸ்), புள்ளிகளில் வரையப்பட்ட ஆர்டினேட்டுகள் அமற்றும் பி, மற்றும் அச்சு பிரிவு எருதுபுள்ளிகளுக்கு இடையில் அமற்றும் பி(படம் 2 ஐப் பார்க்கவும்).

பின்வரும் அறிக்கையை நிரூபிப்போம்.

வளைந்த ட்ரேப்சாய்டு என்பது ஒரு சதுர உருவம், பகுதி பி

ஆதாரம். பிரிவில் தொடர்ந்து இருந்து [ அ, பி] செயல்பாடு ஒருங்கிணைக்கக்கூடியது, பின்னர் எந்த நேர்மறை எண்ணுக்கும் ε அத்தகைய பகிர்வை நீங்கள் குறிப்பிடலாம் டிபிரிவு [ அ, பி], என்ன வேறுபாடு உள்ளது எஸ் - கள் < ε , எங்கே எஸ்மற்றும் கள்- பகிர்வின் மேல் மற்றும் கீழ் தொகைகள் முறையே டி. ஆனாலும் எஸ்மற்றும் கள்முறையே சமமாக இருக்கும் எஸ் ஈமற்றும் எஸ் நான், எங்கே எஸ் ஈமற்றும் எஸ் நான்- படிநிலை உருவங்களின் பகுதிகள் (பலகோணங்கள்), அவற்றில் முதலாவது ஒரு வளைவு ட்ரேப்சாய்டைக் கொண்டுள்ளது, இரண்டாவது ஒரு வளைவு ட்ரேப்சாய்டில் உள்ளது (படம். 2 இந்த படிநிலை புள்ளிவிவரங்களையும் காட்டுகிறது). ஏனெனில் எஸ் ஈ - எஸ் நான் < ε , பின்னர், தேற்றம் 1 இன் அடிப்படையில், வளைவு ட்ரேப்சாய்டு சதுரமானது. மேல் மற்றும் கீழ் தொகைகளின் Δ → 0 வரம்பு சமமாக இருப்பதால் கள் ≤ பி ≤ எஸ், பின்னர் பகுதி பிவளைந்த ட்ரேப்சாய்டை சூத்திரம் (1) பயன்படுத்தி காணலாம்.

கருத்து. செயல்பாடு என்றால் f(எக்ஸ்) பிரிவில் தொடர்ச்சியாகவும் நேர்மறையாகவும் இல்லை [ அ, பி], பின்னர் ஒருங்கிணைப்பின் மதிப்பு எதிர்மறை அடையாளத்துடன் எடுக்கப்பட்ட வளைவு ட்ரெப்சாய்டின் பகுதிக்கு சமமாக இருக்கும், இது செயல்பாட்டின் வரைபடத்தால் வரையறுக்கப்படுகிறது. f(எக்ஸ்), புள்ளிகளில் ஒழுங்குபடுத்துகிறது அமற்றும் பிமற்றும் அச்சு பிரிவு எருதுபுள்ளிகளுக்கு இடையில் அமற்றும் பி. எனவே, என்றால் f(எக்ஸ்) அடையாளத்தை மாற்றுகிறது, பின்னர் அது ஒரு குறிப்பிட்ட அடையாளத்துடன் எடுக்கப்பட்ட அச்சுக்கு மேலேயும் கீழேயும் அமைந்துள்ள வளைவு ட்ரெப்சாய்டுகளின் பகுதிகளின் கூட்டுத்தொகைக்கு சமம் எருது, மற்றும் முந்தைய பகுதிகள் + குறியுடனும், பிந்தையது - அடையாளத்துடனும் எடுக்கப்படுகின்றன.

வளைந்த துறையின் பகுதி

வளைவை விடுங்கள் எல்சமன்பாட்டின் மூலம் துருவ ஒருங்கிணைப்பு அமைப்பில் கொடுக்கப்பட்டுள்ளது ஆர் = ஆர்(θ ), α ≤ θ ≤ β (படம் 3 ஐப் பார்க்கவும்), மற்றும் செயல்பாடு ஆர்(θ ) தொடர்ச்சியானது மற்றும் பிரிவில் எதிர்மறையானது [ α , β ]. ஒரு வளைவால் கட்டப்பட்ட ஒரு தட்டையான உருவம் எல்மற்றும் துருவ அச்சுடன் கோணங்களை உருவாக்கும் இரண்டு கதிர்கள் α மற்றும் β , நாங்கள் அழைப்போம் வளைவுத் துறை.

பின்வரும் அறிக்கையை நிரூபிப்போம். ஒரு வளைவுத் துறை என்பது ஒரு சதுர உருவம், பகுதி பிசூத்திரத்தைப் பயன்படுத்தி கணக்கிட முடியும்

ஆதாரம். பகிர்வைக் கவனியுங்கள் டிபிரிவு [ α , β ] புள்ளிகள் α = θ 0 < θ 1 < ... < θ n = β மற்றும் ஒவ்வொரு பகுதி பிரிவுக்கும் [ θ நான் -1 , θ நான்] ஆரங்கள் குறைந்தபட்சத்திற்கு சமமாக இருக்கும் வட்டப் பிரிவுகளை உருவாக்கவும் ஆர் நான்மற்றும் அதிகபட்சம் ஆர் நான்மதிப்புகள் ஆர்(θ ) பிரிவில் [ θ நான் -1 , θ நான்]. இதன் விளைவாக, இரண்டு விசிறி வடிவ உருவங்களைப் பெறுகிறோம், அவற்றில் முதலாவது வளைவுத் துறையில் உள்ளது, இரண்டாவது வளைவுத் துறையைக் கொண்டுள்ளது (இந்த விசிறி வடிவ புள்ளிவிவரங்கள் படம் 3 இல் காட்டப்பட்டுள்ளன). சுட்டிக்காட்டப்பட்ட விசிறி வடிவ உருவங்களின் பகுதிகள் மற்றும் முறையே சமமாக இருக்கும். இந்த தொகைகளில் முதல் தொகை குறைந்த தொகை என்பதை நினைவில் கொள்க கள்ஒரு குறிப்பிட்ட பகிர்வுக்கான செயல்பாட்டிற்கு டிபிரிவு [ α , β ], மற்றும் இரண்டாவது தொகை மேல் தொகை எஸ்அதே செயல்பாடு மற்றும் அதே பகிர்வுக்கு. செயல்பாடு ஒருங்கிணைக்கக்கூடியதாக இருப்பதால் [ α , β ], பின்னர் வேறுபாடு விரும்பிய அளவுக்கு சிறியதாக இருக்கலாம். உதாரணமாக, எந்த நிலையானது ε > 0 இந்த வித்தியாசத்தை சிறியதாக மாற்றலாம் ε /2. இப்போது உள் விசிறி வடிவ உருவத்தில் பலகோணத்தை பதிப்போம் கே நான்பரப்பளவு கொண்டது எஸ் நான், அதற்காக , மற்றும் வெளிப்புற விசிறி வடிவ உருவத்தைச் சுற்றி ஒரு பலகோணத்தை விவரிக்கிறோம் கே ஈபகுதி எஸ் ஈ, இதற்கு * . வெளிப்படையாக, இந்த பலகோணங்களில் முதலாவது ஒரு வளைவுத் துறையில் பொறிக்கப்பட்டுள்ளது, இரண்டாவது அதைச் சுற்றி வளைக்கப்பட்டுள்ளது. ஏற்றத்தாழ்வுகள் செல்லுபடியாகும் என்பதால்

வரையறை. F (b) - F (a) என்ற வித்தியாசம் f (x) செயல்பாட்டின் ஒருங்கிணைப்பு என்று அழைக்கப்படுகிறது [ a ; b ] மற்றும் பின்வருமாறு குறிக்கப்படுகிறது: = F (b) - F (a) - Newton-Leibniz சூத்திரம்.

ஒருங்கிணைப்பின் வடிவியல் பொருள்.

இடைவெளியில் ஒரு தொடர்ச்சியான நேர்மறை வரைபடத்தால் கட்டுப்படுத்தப்பட்ட ஒரு வளைவு ட்ரேப்சாய்டின் பகுதி [a; b ] செயல்பாடுகள் f (x), ஆக்ஸ் அச்சு மற்றும் கோடுகள் x=a மற்றும் x= b:

ஒருங்கிணைந்த பகுதியைப் பயன்படுத்தி பகுதிகளைக் கணக்கிடுதல்.

1. இடைவெளியில் ஒரு தொடர்ச்சியான எதிர்மறை வரைபடத்தால் வரையறுக்கப்பட்ட உருவத்தின் பரப்பளவு [a; b ] செயல்பாடுகள் f (x), ஆக்ஸ் அச்சு மற்றும் கோடுகள் x=a மற்றும் x= b:

2. தொடர்ச்சியான செயல்பாடுகள் f (x) மற்றும் வரிகள் x=a, x= b ஆகியவற்றின் வரைபடங்களால் வரையறுக்கப்பட்ட உருவத்தின் பரப்பளவு:

3. தொடர்ச்சியான செயல்பாடுகளின் வரைபடங்களால் வரையறுக்கப்பட்ட உருவத்தின் பரப்பளவு f (x) மற்றும்:

4. தொடர்ச்சியான செயல்பாடுகள் f (x) மற்றும் ஆக்ஸ் அச்சின் வரைபடங்களால் வரையறுக்கப்பட்ட உருவத்தின் பரப்பளவு:

"ஒருங்கிணைப்பு. ஒருங்கிணைந்த பகுதியைப் பயன்படுத்தி பகுதிகளின் கணக்கீடு" என்ற தலைப்பில் சிக்கல்கள் மற்றும் சோதனைகள்

• ஒருங்கிணைந்த

  பாடங்கள்: 4 பணிகள்: 13 தேர்வுகள்: 1

• ஒருங்கிணைப்புகளைப் பயன்படுத்தி பகுதிகளைக் கணக்கிடுதல் - ஆண்டிடெரிவேட்டிவ் மற்றும் ஒருங்கிணைந்த தரம் 11

  பாடங்கள்: 1 பணிகள்: 10 தேர்வுகள்: 1

• ஆண்டிடெரிவேட்டிவ் - ஆண்டிடெரிவேட்டிவ் மற்றும் ஒருங்கிணைந்த தரம் 11

  பாடங்கள்: 1 பணிகள்: 11 தேர்வுகள்: 1

• பிளானிமெட்ரி: நீளம் மற்றும் பகுதிகளின் கணக்கீடு

  பணிகள்: 7

• கணக்கீடுகள் மற்றும் மாற்றங்கள் - கணிதத்தில் ஒருங்கிணைந்த மாநிலத் தேர்வுக்கான தயாரிப்பு, கணிதத்தில் ஒருங்கிணைந்த மாநிலத் தேர்வு

  பணிகள்: 10

கொடுக்கப்பட்ட கோடுகளால் வரையறுக்கப்பட்ட ஒரு உருவத்தின் பகுதியைக் கணக்கிடத் தொடங்குவதற்கு முன், இந்த உருவத்தை ஒரு ஒருங்கிணைப்பு அமைப்பில் சித்தரிக்க முயற்சிக்கவும். இது சிக்கலைத் தீர்ப்பதை மிகவும் எளிதாக்கும்.

இந்த தலைப்பில் கோட்பாட்டுப் பொருட்களைப் படிப்பது, ஆண்டிடெரிவேட்டிவ் மற்றும் இன்டெகிரால் என்ற கருத்துகளில் தேர்ச்சி பெறவும், அவற்றுக்கிடையேயான தொடர்பைப் புரிந்து கொள்ளவும், ஒருங்கிணைந்த கால்குலஸின் எளிய நுட்பத்தை மாஸ்டர் செய்யவும், மேலும் செயல்பாடுகளின் வரைபடங்களால் வரையறுக்கப்பட்ட புள்ளிவிவரங்களின் பகுதிகளைக் கணக்கிடுவதற்கு ஒருங்கிணைப்பைப் பயன்படுத்த கற்றுக்கொள்ளவும் உங்களுக்கு வாய்ப்பளிக்கிறது. .

எடுத்துக்காட்டுகள்.

1. ஒருங்கிணைந்த கணக்கீடு

தீர்வு:

பதில்: 0.

2. கோடுகளால் கட்டப்பட்ட உருவத்தின் பகுதியைக் கண்டறியவும்

a) f(எக்ஸ்) = 2 எக்ஸ் – எக்ஸ் 2 மற்றும் x-அச்சு

தீர்வு: f(x) = 2x - x 2 செயல்பாட்டின் வரைபடம் ஒரு பரவளையமாகும். உச்சி: (1; 1).

பதில்:(சதுர அலகுகள்).

எண்.___ தேதி________

பொருள்:கர்விலினியர் ட்ரேப்சாய்டு மற்றும் அதன் பகுதி பி

பாடம் நோக்கங்கள்: வளைந்த ட்ரேப்சாய்டு மற்றும் அதன் பகுதியை வரையறுக்கவும், வளைந்த ட்ரேப்சாய்டின் பகுதியை கணக்கிட கற்றுக்கொள்ளுங்கள்.

வகுப்புகளின் போது

1. நிறுவன தருணம்.

மாணவர்களை வாழ்த்துதல், பாடத்திற்கான வகுப்பின் தயார்நிலையை சரிபார்த்தல், மாணவர்களின் கவனத்தை ஒழுங்கமைத்தல், பாடத்தின் பொதுவான குறிக்கோள்கள் மற்றும் அதன் திட்டத்தை வெளிப்படுத்துதல்.

2. வீட்டுப்பாடம் சரிபார்க்கும் நிலை.

குறிக்கோள்கள்: அனைத்து மாணவர்களாலும் வீட்டுப்பாடத்தின் செயல்திறன் பற்றிய சரியான, முழுமை மற்றும் விழிப்புணர்வை நிறுவுதல், மாணவர்களின் அறிவு மற்றும் செயல்பாட்டு முறைகளில் உள்ள இடைவெளிகளைக் கண்டறிதல். சிரமங்களுக்கான காரணங்களைத் தீர்மானித்தல் மற்றும் கண்டறியப்பட்ட இடைவெளிகளை அகற்றவும்.

3. புதுப்பிப்பு நிலை.

குறிக்கோள்கள்: பள்ளி மாணவர்களின் கற்றலின் ஊக்கத்தை உறுதி செய்தல், பாடத்தின் இலக்குகளை தீர்மானிக்க கூட்டு நடவடிக்கைகளில் சேர்ப்பது. மாணவர்களின் அகநிலை அனுபவத்தைப் புதுப்பிக்கவும்.

அடிப்படை கருத்துகள் மற்றும் சூத்திரங்களை நினைவில் கொள்வோம்.

வரையறை.செயல்பாடு y=f(x), x (a,b),செயல்பாட்டின் ஆண்டிடெரிவேட்டிவ் என்று அழைக்கப்படுகிறது y=f(x), x (a,b),அனைவருக்கும் என்றால் எக்ஸ் (a,b)சமத்துவம் உள்ளது

எஃப் (x)=f(x).

கருத்து.என்றால் f(எக்ஸ்)செயல்பாட்டிற்கு ஒரு ஆன்டிடெரிவேடிவ் உள்ளது f(x), பின்னர் எந்த மாறிலிக்கும் உடன், F(x)+Cஎன்பதற்கான ஒரு எதிர்ப்பொருளாகவும் உள்ளது f(x)

ஒரு செயல்பாட்டின் அனைத்து ஆன்டிடெரிவேடிவ்களையும் கண்டுபிடிப்பதில் சிக்கல் f(x)ஒருங்கிணைப்பு என்று அழைக்கப்படுகிறது, மேலும் அனைத்து ஆண்டிடெரிவேடிவ்களின் தொகுப்பு செயல்பாட்டிற்கான காலவரையற்ற ஒருங்கிணைப்பு என்று அழைக்கப்படுகிறது. f(x)மூலம் dxமற்றும் நியமிக்கப்பட்டுள்ளது

பின்வரும் பண்புகள் நடைபெறுகின்றன:

1 ;

2 என்றால் C=கான்ஸ்ட், பின்னர்
;

3
.

கருத்து.பள்ளிக் கணிதப் பாடங்களில், "காலவரையற்ற ஒருங்கிணைப்பு" என்ற சொல் பயன்படுத்தப்படுவதில்லை; மாறாக, "அனைத்து ஆண்டிடெரிவேடிவ்களின் தொகுப்பு" என்று கூறுகின்றனர்.

இங்கே காலவரையற்ற ஒருங்கிணைப்புகளின் அட்டவணை உள்ளது.

எடுத்துக்காட்டு 1.ஒரு செயல்பாட்டிற்கான ஆன்டிடெரிவேட்டிவ் ஒன்றைக் கண்டறியவும்
, புள்ளி வழியாக செல்கிறது எம்(2;4).

தீர்வு.ஒரு செயல்பாட்டின் அனைத்து ஆண்டிடெரிவேடிவ்களின் தொகுப்பு
ஒரு காலவரையற்ற ஒருங்கிணைப்பு உள்ளது
. ஒருங்கிணைந்த 1 மற்றும் 2 பண்புகளைப் பயன்படுத்தி அதைக் கணக்கிடுவோம். எங்களிடம் உள்ளது:

அனைத்து ஆண்டிடெரிவேடிவ்களின் தொகுப்பும் செயல்பாடுகளின் குடும்பத்தால் வழங்கப்படுகிறது என்பதைக் கண்டறிந்தோம் y=F(x)+C, அது y=x 3 – 2x+C, எங்கே உடன்- தன்னிச்சையான மாறிலி.

ஆன்டிடெரிவேட்டிவ் புள்ளி வழியாக செல்கிறது என்பதை அறிவது எம்(2;4), அதன் ஒருங்கிணைப்புகளை முந்தைய வெளிப்பாட்டிற்கு மாற்றியமைத்து கண்டுபிடிக்கவும் உடன்.

4=2 3 –2 2+உடன்  உடன்=4–8+4; உடன்=0.

பதில்: F(x)=x 3 - 2எக்ஸ்- விரும்பிய ஆன்டிடெரிவேடிவ்.

4. புதிய கருத்துக்கள் மற்றும் செயல் முறைகளின் உருவாக்கம்.

குறிக்கோள்கள்: மாணவர்கள் படிக்கும் பொருளை உணர்ந்து, புரிந்துகொள்வது மற்றும் நினைவில் வைத்திருப்பதை உறுதி செய்தல். படித்த பொருளை மீண்டும் உருவாக்கும் முறைகளில் மாணவர்கள் தேர்ச்சி பெறுவதை உறுதிசெய்து, பெறப்படும் கருத்துக்கள், சட்டங்கள், விதிகள் மற்றும் சூத்திரங்கள் பற்றிய தத்துவ புரிதலை ஊக்குவிக்கவும். மாணவர்களால் ஆய்வு செய்யப்பட்ட பொருளின் சரியான தன்மை மற்றும் விழிப்புணர்வை நிறுவுதல், முதன்மை புரிதலில் உள்ள இடைவெளிகளைக் கண்டறிதல் மற்றும் திருத்தங்களைச் செய்தல். மாணவர்கள் தங்கள் அகநிலை அனுபவத்தை அறிவியல் அறிவின் அறிகுறிகளுடன் தொடர்புபடுத்துவதை உறுதி செய்யவும்.

விமான உருவங்களின் பகுதிகளைக் கண்டறிதல்

ஒரு விமான உருவத்தின் பகுதியைக் கண்டறிவதில் உள்ள சிக்கல், ஆண்டிடெரிவேடிவ்களை (ஒருங்கிணைப்பு) கண்டுபிடிப்பதில் உள்ள சிக்கலுடன் நெருக்கமாக தொடர்புடையது. அதாவது: ஒரு செயல்பாட்டின் வரைபடத்தால் வரையறுக்கப்பட்ட வளைவு ட்ரேப்சாய்டின் பகுதிy=f(x) (f(x)> 0) நேராகx=a; x=b; y= 0, செயல்பாட்டிற்கான ஆண்டிடெரிவேட்டிவ் மதிப்புகளுக்கு இடையிலான வேறுபாட்டிற்கு சமம்y=f(x) புள்ளிகளில்பி மற்றும்அ :

S=F(b)–F(a)

ஒரு திட்டவட்டமான ஒருங்கிணைப்பின் வரையறையை வழங்குவோம்.

பற்றி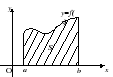
வரையறை.செயல்படட்டும் y=f(x)வரையறுக்கப்பட்ட மற்றும் ஒருங்கிணைக்கக்கூடிய இடைவெளியில் [ a,b] போகட்டும் F(x)- அதன் சில முன்மாதிரிகள். பின்னர் எண் F(b)–F(a)இன் ஒருங்கிணைப்பு என்று அழைக்கப்படுகிறது ஏமுன் பிசெயல்பாடுகள் f(x)மற்றும் நியமிக்கப்பட்டுள்ளது

.

சமத்துவம்
நியூட்டன்-லீப்னிஸ் சூத்திரம் என்று அழைக்கப்படுகிறது.

இந்த சூத்திரம் ஒரு விமான உருவத்தின் பரப்பளவைக் கண்டறிவதில் உள்ள சிக்கலை ஒரு ஒருங்கிணைப்புடன் இணைக்கிறது.

பொதுவாக, செயல்பாடு வரைபடங்களால் எண்ணிக்கை வரையறுக்கப்பட்டிருந்தால் y=f(x);y=g(x) (f(x)>g(x)) மற்றும் நேராக x=a;x=b, அதன் பரப்பளவு இதற்கு சமம்:

.

எடுத்துக்காட்டு 2.செயல்பாட்டின் வரைபடத்தில் எந்த புள்ளியில் y=x 2 + 1 நீங்கள் ஒரு தொடுகோடு வரைய வேண்டும், இதனால் இந்த செயல்பாட்டின் வரைபடம் மற்றும் நேர் கோடுகளால் உருவாக்கப்பட்ட உருவத்திலிருந்து அது துண்டிக்கப்படும் y= 0, x= 0, x=மிகப்பெரிய பரப்பளவைக் கொண்ட 1 ட்ரெப்சாய்டு?

தீர்வு.விடுங்கள் எம் 0 (எக்ஸ் 0 ,ஒய் 0 ) - செயல்பாட்டு வரைபடத்தின் புள்ளி y=x 2 + 1, இதில் தேவையான தொடுகோடு வரையப்பட்டது.

தொடுகோடு சமன்பாட்டைக் கண்டுபிடிப்போம் y=y 0 +f (எக்ஸ் 0 )(x–x 0 ) .

எங்களிடம் உள்ளது:

அதனால் தான்

.

ட்ரேப்சாய்டின் பகுதியைக் கண்டறியவும் OABC.

.

பி– நேர்கோட்டுடன் தொடுகோடு வெட்டும் புள்ளி x= 1 

செயல்பாட்டின் மிகப்பெரிய மதிப்பைக் கண்டறியும் பணி குறைக்கப்பட்டது

எஸ்(எக்ஸ்)=–x 2 +x+பிரிவில் 1. நாம் கண்டுபிடிப்போம் எஸ் (எக்ஸ்)=– 2x+ 1. நிபந்தனையிலிருந்து முக்கியமான புள்ளியைக் கண்டறியவும் எஸ் (எக்ஸ்)= 0  x=.

செயல்பாடு அதன் மிகப்பெரிய மதிப்பை அடைவதைக் காண்கிறோம் x=. நாம் கண்டுபிடிப்போம்
.

பதில்:தொடுகோடு புள்ளியில் வரையப்பட வேண்டும்
.

அதன் வடிவியல் அர்த்தத்தின் அடிப்படையில் ஒரு ஒருங்கிணைப்பைக் கண்டுபிடிப்பதில் சிக்கல் அடிக்கடி நிகழ்கிறது என்பதை நினைவில் கொள்க. இந்த பிரச்சனை எவ்வாறு தீர்க்கப்படுகிறது என்பதை ஒரு எடுத்துக்காட்டுடன் காண்பிப்போம்.

எடுத்துக்காட்டு 4.ஒருங்கிணைப்பின் வடிவியல் பொருளைப் பயன்படுத்தி, கணக்கிடுங்கள்

ஏ )
; b)
.

தீர்வு.

A)
- கோடுகளால் கட்டுப்படுத்தப்பட்ட வளைந்த ட்ரேப்சாய்டின் பரப்பளவிற்கு சமம்.

பி மாற்றுவோம்

- மையத்துடன் வட்டத்தின் மேல் பாதி ஆர்(1;0) மற்றும் ஆரம் ஆர்= 1.

அதனால் தான்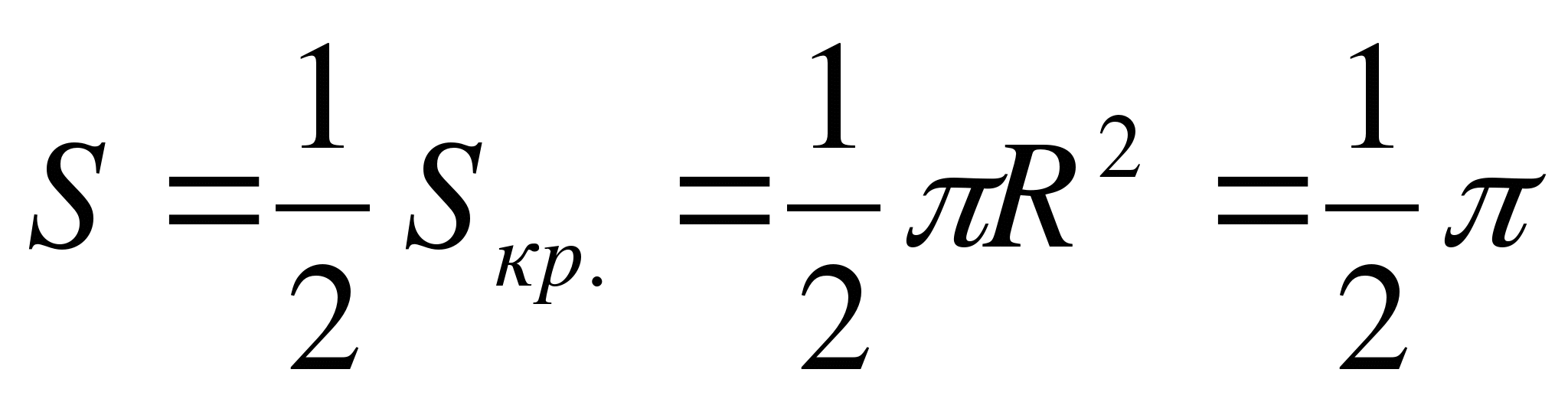
.

பதில்:
.

b) இதேபோல் வாதிடுகையில், வரைபடங்களால் வரையறுக்கப்பட்ட பகுதியை உருவாக்குவோம் .2 – 2x+ 2, புள்ளிகளில் அதன் தொடுகோடு ஏ
, பி(4;2)

y=–9எக்ஸ்- 59, பரவளையம் y= 3எக்ஸ் 2 +கோடாரி+ 1, புள்ளியில் உள்ள பரவளையத்தின் தொடுகோடு என்று தெரிந்தால் x=– 2 அச்சுடன் உள்ளது எருதுகோண அளவு arctg 6.

கண்டுபிடி ஏ, ஒரு வளைவு ட்ரேப்சாய்டின் பரப்பளவு கோடுகளால் கட்டப்பட்டுள்ளது என்பது தெரிந்தால் y= 3எக்ஸ் 3 + 2x, x=a, y= 0 என்பது ஒன்றுக்கு சமம்.

பரவளையத்தால் கட்டுப்படுத்தப்பட்ட உருவத்தின் மிகச்சிறிய பகுதியைக் கண்டறியவும் y=x 2 + 2எக்ஸ்- 3 மற்றும் நேராக y=kx+ 1.

6. வீட்டுப்பாட தகவல் நிலை.

குறிக்கோள்கள்: வீட்டுப்பாடத்தை முடிப்பதற்கான நோக்கம், உள்ளடக்கம் மற்றும் முறைகளை மாணவர்கள் புரிந்துகொள்வதை உறுதிசெய்ய. எண். 18, 19,20,21 ஒற்றைப்படை

7. பாடத்தை சுருக்கவும்.

குறிக்கோள்: வகுப்பு மற்றும் தனிப்பட்ட மாணவர்களின் பணியின் தரமான மதிப்பீட்டை வழங்குதல்.