مفهوم شبه منحرف منحني. الموضوع: شبه منحرف منحني الخطوط ومساحته. تكوين مفاهيم وأساليب عمل جديدة

الشكل الذي يحده الرسم البياني للدالة المستمرة غير السالبة $f(x)$ على القطعة $$ والخطوط $y=0، \ x=a$ و $x=b$ يسمى شبه منحرف منحني الخطوط.

يتم حساب مساحة شبه المنحرف المنحني المقابل بواسطة الصيغة:

$S=\int\limits_(a)^(b)(f(x)dx).$ (*)

سنقوم بتقسيم المسائل بشكل مشروط للعثور على مساحة شبه منحرف منحني الأضلاع إلى أنواع $4$. دعونا ننظر إلى كل نوع بمزيد من التفصيل.

النوع الأول: شبه منحرف منحني محدد بشكل صريح.ثم قم بتطبيق الصيغة (*) على الفور.

على سبيل المثال، ابحث عن مساحة شبه منحرف منحني يحدها الرسم البياني للدالة $y=4-(x-2)^(2)$ والخطوط $y=0, \ x=1$ و$x =3$.

دعونا نرسم هذا شبه المنحرف المنحني.

باستخدام الصيغة (*)، نجد مساحة شبه المنحرف المنحني هذا.

$S=\int\limits_(1)^(3)(\left(4-(x-2)^(2)\right)dx)=\int\limits_(1)^(3)(4dx)- \int\limits_(1)^(3)((x-2)^(2)dx)=4x|_(1)^(3) – \left.\frac((x-2)^(3) )(3)\يمين|_(1)^(3)=$

$=4(3-1)-\frac(1)(3)\left((3-2)^(3)-(1-2)^(3)\right)=4 \cdot 2 – \frac (1)(3)\يسار((1)^(3)-(-1)^(3)\يمين) = 8 – \frac(1)(3)(1+1) =$

$=8-\frac(2)(3)=7\frac(1)(3)$ (الوحدات$^(2)$).

النوع الثاني: شبه المنحرف المنحني محدد ضمنيا.في هذه الحالة، الخطوط المستقيمة $x=a, \ x=b$ عادةً ما تكون غير محددة أو محددة جزئيًا. في هذه الحالة، تحتاج إلى العثور على نقاط تقاطع الدالتين $y=f(x)$ و$y=0$. ستكون هذه النقاط هي النقاط $a$ و$b$.

على سبيل المثال، ابحث عن مساحة الشكل المحدود بالرسوم البيانية للدالتين $y=1-x^(2)$ و$y=0$.

دعونا نجد نقاط التقاطع. للقيام بذلك، نساوي الأطراف اليمنى للدوال.

وبالتالي، $a=-1$ و$b=1$. دعونا نرسم هذا شبه المنحرف المنحني.

دعونا نجد مساحة هذا شبه المنحرف المنحني.

$S=\int\limits_(-1)^(1)(\left(1-x^(2)\right)dx)=\int\limits_(-1)^(1)(1dx)-\int \limits_(-1)^(1)(x^(2)dx)=x|_(-1)^(1) – \left.\frac(x^(3))(3)\right|_ (-1)^(1)=$

$=(1-(-1))-\frac(1)(3)\left(1^(3)-(-1)^(3)\right)=2 – \frac(1)(3) \left(1+1\right) = 2 – \frac(2)(3) = 1\frac(1)(3)$ (الوحدات$^(2)$).

النوع الثالث: مساحة الشكل المحدد بتقاطع دالتين متصلتين غير سالبتين.لن يكون هذا الشكل شبه منحرف منحني، مما يعني أنه لا يمكنك حساب مساحته باستخدام الصيغة (*). كيف تكون؟اتضح أنه يمكن إيجاد مساحة هذا الشكل بالفرق بين مساحات شبه المنحرف المنحني التي تحدها الدالة العلوية و$y=0$ ($S_(uf)$)، والدالة السفلية و$y =0$ ($S_(lf)$)، حيث يتم لعب دور $x=a, \ x=b$ بواسطة إحداثيات $x$ لنقاط تقاطع هذه الوظائف، أي.

$S=S_(uf)-S_(lf)$. (**)

الشيء الأكثر أهمية عند حساب هذه المناطق هو عدم "تفويت" اختيار الوظائف العلوية والسفلية.

على سبيل المثال، ابحث عن مساحة الشكل المحدود بالدالتين $y=x^(2)$ و$y=x+6$.

دعونا نجد نقاط التقاطع لهذه الرسوم البيانية:

وفقا لنظرية فييتا،

$x_(1)=-2,\x_(2)=3.$

أي $a=-2,\b=3$. دعونا نرسم الشكل:

وبالتالي، فإن الدالة العلوية هي $y=x+6$، والدالة السفلية هي $y=x^(2)$. بعد ذلك، نجد $S_(uf)$ و$S_(lf)$ باستخدام الصيغة (*).

$S_(uf)=\int\limits_(-2)^(3)((x+6)dx)=\int\limits_(-2)^(3)(xdx)+\int\limits_(-2 )^(3)(6dx)=\left.\frac(x^(2))(2)\يمين|_(-2)^(3) + 6x|_(-2)^(3)= 32 .5$ (الوحدات$^(2)$).

$S_(lf)=\int\limits_(-2)^(3)(x^(2)dx)=\left.\frac(x^(3))(3)\right|_(-2) ^(3) = \frac(35)(3)$ (الوحدات$^(2)$).

لنعوض بما وجدناه في (**) ونحصل على:

$S=32.5-\frac(35)(3)= \frac(125)(6)$ (الوحدات$^(2)$).

النوع الرابع: مساحة الشكل المحدود بوظيفة أو وظائف لا تحقق شرط عدم السالبة.من أجل العثور على مساحة هذا الشكل، عليك أن تكون متناظرا حول محور $Ox$ ( بعبارة أخرى،ضع "السلبيات" أمام الوظائف) اعرض المنطقة، وباستخدام الطرق الموضحة في الأنواع من الأول إلى الثالث، ابحث عن مساحة المنطقة المعروضة. ستكون هذه المنطقة هي المنطقة المطلوبة. أولاً، قد يتعين عليك العثور على نقاط تقاطع الرسوم البيانية للدالة.

على سبيل المثال، ابحث عن مساحة الشكل المحدود بالرسوم البيانية للدالتين $y=x^(2)-1$ و$y=0$.

لنجد نقاط التقاطع للرسوم البيانية للوظائف:

أولئك. $a=-1$، و$b=1$. دعونا نرسم المنطقة.

دعونا نعرض المنطقة بشكل متماثل:

$y=0 \ \Rightarrow \ y=-0=0$

$y=x^(2)-1 \ \Rightarrow \ y= -(x^(2)-1) = 1-x^(2)$.

والنتيجة هي شبه منحرف منحني الأضلاع يحده الرسم البياني للدالة $y=1-x^(2)$ و $y=0$. هذه مشكلة للعثور على شبه منحرف منحني من النوع الثاني. لقد قمنا بحلها بالفعل. كانت الإجابة: $S= 1\frac(1)(3)$ (الوحدات $^(2)$). وهذا يعني أن مساحة شبه المنحرف المنحني المطلوب تساوي:

$S=1\frac(1)(3)$ (الوحدات$^(2)$).

مساحة شبه منحرف منحني

شبه منحرف منحني الأضلاعهو رقم يحده رسم بياني معطى على القطعة [ أ, ب] وظيفة مستمرة وغير سلبية F(س) ، الإحداثيات المرسومة عند النقاط أو ب، وقطعة المحور ثوربين النقاط أو ب(انظر الشكل 2).

دعونا نثبت العبارة التالية.

شبه المنحرف المنحني هو شكل مربع، مساحة ص

دليل. منذ المستمر على المقطع [ أ, ب] الدالة قابلة للتكامل، ثم لأي رقم موجب ε يمكنك تحديد مثل هذا القسم تشريحة [ أ, ب]، ماهو الفرق س - س < ε ، أين سو س- مجموع القسم العلوي والسفلي على التوالي ت. لكن سو سمتساوية على التوالي س دو س أنا، أين س دو س أنا- مساحات من الأشكال المتدرجة (المضلعات)، أولها يحتوي على شبه منحرف منحني الأضلاع، والثاني موجود في شبه منحرف منحني الأضلاع (الشكل 2 يوضح أيضًا هذه الأشكال المتدرجة). لأن س د - س أنا < ε إذن، بموجب النظرية 1، فإن شبه المنحرف المنحني يكون مربعًا. نظرًا لأن الحد الأقصى لـ Δ → 0 للمجموعين العلوي والسفلي يساوي س ≤ ص ≤ س، ثم المنطقة صيمكن إيجاد شبه المنحرف المنحني باستخدام الصيغة (1).

تعليق. إذا كانت الوظيفة F(س) مستمر وغير موجب على المقطع [ أ, ب]، فإن قيمة التكامل تساوي مساحة شبه منحرف منحني الأضلاع مأخوذة بعلامة سلبية، محدودة بالرسم البياني للدالة F(س) ، الإحداثيات في النقاط أو بوقطعة المحور ثوربين النقاط أو ب. لذلك، إذا F(س) علامة التغييرات، فهي تساوي مجموع مساحات شبه المنحرف المنحني الموجود أعلى وأسفل المحور المأخوذ بعلامة معينة ثور، ويتم أخذ مساحات الأول بعلامة +، ومساحات الأخير بعلامة -.

مساحة القطاع المنحني

دع المنحنى ليتم تقديمه في نظام الإحداثيات القطبية بواسطة المعادلة ص = ص(θ ), α ≤ θ ≤ β (انظر الشكل 3)، والوظيفة ص(θ ) مستمر وغير سالب على المقطع [ α , β ]. شكل مسطح يحده منحنى لوشعاعان يصنعان زوايا مع المحور القطبي α و β ، سنطالب القطاع المنحني.

دعونا نثبت العبارة التالية. القطاع المنحني هو شكل مربع، مساحة صوالتي يمكن حسابها باستخدام الصيغة

دليل. النظر في التقسيم تشريحة [ α , β ] النقاط α = θ 0 < θ 1 < ... < θ ن = β ولكل جزء جزئي [ θ أنا -1 , θ أنا] إنشاء قطاعات دائرية نصف أقطارها تساوي الحد الأدنى ص أناوالحد الأقصى ر أناقيم ص(θ ) على الجزء [ θ أنا -1 , θ أنا]. ونتيجة لذلك، نحصل على شكلين على شكل مروحة، الأول منهما موجود في القطاع المنحني، والثاني يحتوي على القطاع المنحني (تظهر هذه الأشكال على شكل مروحة في الشكل 3). مساحات الأشكال المروحية المشار إليها تساوي و على التوالي. لاحظ أن أول هذه المبالغ هو المبلغ الأدنى سلوظيفة لقسم محدد تشريحة [ α , β ]، والمجموع الثاني هو المبلغ الأعلى سلنفس الوظيفة ونفس القسم. بما أن الوظيفة قابلة للتكامل في المقطع [ α , β ]، فيمكن أن يكون الفرق صغيرًا حسب الرغبة. على سبيل المثال، لأي ثابت ε > 0 يمكن تصغير هذا الاختلاف ε /2. دعونا الآن نكتب مضلعًا في الشكل الداخلي على شكل مروحة س أنامع المنطقة س أنا، والتي وصفنا مضلعًا حول الشكل الخارجي على شكل مروحة س دمنطقة س د، لأي منهم * . ومن الواضح أن أول هذه المضلعات محفور في قطاع منحني الأضلاع، والثاني محاط حوله. وبما أن عدم المساواة صحيحة

تعريف.الفرق F (b) – F (a) يسمى تكامل الدالة f (x) على الفترة [ a ; b ] ويرمز له على النحو التالي: = F (b) – F (a) – صيغة نيوتن-لايبنتز.

المعنى الهندسي للتكامل.

مساحة شبه منحرف منحني الأضلاع يحدها رسم بياني إيجابي مستمر على الفاصل الزمني [أ؛ b ] وظائف f (x)، ومحور الثور والخطين x=a وx= b:

حساب المساحات باستخدام التكامل.

1.مساحة الشكل محدودة برسم بياني سلبي مستمر على الفاصل الزمني [أ؛ b ] وظائف f (x)، ومحور الثور والخطين x=a وx= b:

2. مساحة الشكل محدودة بالرسوم البيانية للوظائف المستمرة f (x) والخطوط x=a، x= b:

3. مساحة الشكل محدودة بالرسوم البيانية للوظائف المستمرة f (x) و:

4. مساحة الشكل محدودة بالرسوم البيانية للدوال المستمرة f (x) ومحور الثور:

مسائل واختبارات حول موضوع "التكامل. حساب المساحات باستخدام التكامل"

• أساسي

  الدروس: 4 واجبات: 13 اختبار: 1

• حساب المساحات باستخدام التكاملات - المشتق العكسي والتكامل الصف 11

  الدروس: 1 الواجبات: 10 الاختبارات: 1

• مشتق مضاد - المشتق العكسي والتكامل الصف 11

  الدروس: 1 الواجبات: 11 الاختبارات: 1

• قياس المساحة: حساب الأطوال والمساحات

  المهام: 7

• الحسابات والتحويلات - التحضير لامتحان الدولة الموحد في الرياضيات امتحان الدولة الموحد في الرياضيات

  المهام: 10

قبل البدء في حساب مساحة الشكل المحدود بخطوط معينة، حاول تصوير هذا الشكل في نظام الإحداثيات. وهذا سيجعل حل المشكلة أسهل بكثير.

تمنحك دراسة المواد النظرية حول هذا الموضوع الفرصة لإتقان مفهومي المشتقة العكسية والتكامل، وفهم العلاقة بينهما، وإتقان أبسط تقنية لحساب التكامل، وتعلم كيفية تطبيق التكامل لحساب مساحات الأشكال التي تحددها الرسوم البيانية للوظائف .

أمثلة.

1. احسب التكامل

حل:

إجابة: 0.

2. أوجد مساحة الشكل المحدد بالخطوط

أ) F(س) = 2 X – X 2 والمحور السيني

حل:الرسم البياني للدالة f(x) = 2x - x 2 هو قطع مكافئ. قمة الرأس : (1 ؛ 1).

إجابة:(وحدات مربعة).

رقم ___ التاريخ________

موضوع:شبه منحرف منحني الخطوط ومساحته ب

أهداف الدرس: تحديد شبه منحرف منحني ومساحته، وتعلم حساب مساحة شبه منحرف منحني.

خلال الفصول الدراسية

1. اللحظة التنظيمية.

تحية الطلاب، والتأكد من جاهزية الفصل للدرس، وتنظيم انتباه الطلاب، والكشف عن الأهداف العامة للدرس وخطته.

2. مرحلة فحص الواجبات المنزلية.

الأهداف: إثبات صحة واكتمال ووعي أداء الواجب المنزلي من قبل جميع الطلاب، وتحديد الفجوات في معرفة الطلاب وأساليب النشاط. تحديد أسباب الصعوبات وإزالة أي ثغرات موجودة.

3. مرحلة التحديث.

الأهداف: ضمان تحفيز تعلم أطفال المدارس وإدراجهم في الأنشطة المشتركة لتحديد أهداف الدرس. تحديث التجربة الذاتية للطلاب.

دعونا نتذكر المفاهيم والصيغ الأساسية.

تعريف.وظيفة ص=F(خ)، س (أ، ب)،يسمى المشتق العكسي للدالة ص = و (س)، س (أ، ب)،إذا للجميع س (أ،ب)المساواة تحمل

F (س)=و(خ).

تعليق.لو F(خ)هناك مشتق عكسي للوظيفة و (خ)، ثم لأي ثابت مع, و(خ)+جهو أيضا مشتق مضاد ل و (خ).

مشكلة إيجاد جميع المشتقات العكسية للدالة و (خ)يسمى التكامل، ومجموعة جميع المشتقات العكسية تسمى التكامل غير المحدد للدالة و (خ)بواسطة dxويتم تعيينه

تحدث الخصائص التالية:

1 . ;

2 . لو ج=كونست إذن
;

3 .
.

تعليق.في دورات الرياضيات المدرسية، لا يتم استخدام مصطلح "التكامل غير المحدد"؛ وبدلاً من ذلك، يقولون "مجموعة جميع المشتقات العكسية".

فيما يلي جدول التكاملات غير المحددة.

مثال 1.ابحث عن المشتقة العكسية للدالة
، مرورا بالنقطة م(2;4).

حل.مجموعة جميع المشتقات العكسية للدالة
هناك تكامل غير محدد
. لنحسبها باستخدام خصائص التكامل 1 و2. لدينا:

لقد وجدنا أن مجموعة جميع المشتقات العكسية تعطى من خلال عائلة من الوظائف ص=F(س)+C، إنه ص=س 3 – 2س+ج، أين مع- ثابت تعسفي.

مع العلم أن المشتق العكسي يمر بالنقطة م(2؛4)، استبدل إحداثياته ​​في التعبير السابق وابحث عنه مع.

4=2 3 –2 2+مع  مع=4–8+4; مع=0.

إجابة: و(س)=س 3 - 2س- المشتق العكسي المطلوب.

4. تكوين مفاهيم وأساليب عمل جديدة.

الأهداف: التأكد من أن الطلاب يدركون ويستوعبون ويتذكرون المادة التي تتم دراستها. التأكد من إتقان الطلاب لأساليب إعادة إنتاج المادة المدروسة، وتعزيز الفهم الفلسفي للمفاهيم والقوانين والقواعد والصيغ التي يتم اكتسابها. إثبات صحة ووعي الطلاب بالمادة المدروسة، وتحديد الفجوات في الفهم الأولي، وإجراء التصحيحات. التأكد من أن الطلاب يربطون تجربتهم الشخصية بعلامات المعرفة العلمية.

إيجاد مساحات الأشكال المستوية

ترتبط مشكلة إيجاد مساحة الشكل المستوي ارتباطًا وثيقًا بمشكلة إيجاد المشتقات العكسية (التكامل). وهي: مساحة شبه منحرف منحني محدود بالرسم البياني للدالةص = و (س) (و(خ)> 0) مستقيمس=أ; س=ب; ص= 0، يساوي الفرق بين قيم المشتق العكسي للدالةص = و (س) في النقاطب وأ :

S=F(ب)–F(أ)

دعونا نعطي تعريف التكامل المحدد.

عن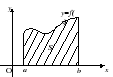
تعريف.دع الوظيفة ص = و (س)محددة وقابلة للتكامل على الفاصل الزمني [ أ، ب] دعها تذهب و(خ)- بعض نماذجها الأولية. ثم الرقم و(ب)–و(أ)يسمى تكامل أقبل بالمهام و (خ)ويتم تعيينه

.

المساواة
تسمى صيغة نيوتن-لايبنتز.

تربط هذه الصيغة مشكلة إيجاد مساحة الشكل المستوي بالتكامل.

بشكل عام، إذا كان الرقم محدودا بالرسوم البيانية الوظيفية ص = و (س);ص = ز (س) (و(خ)>ز(خ)) ومستقيم س=أ;س = ب، فإن مساحتها تساوي:

.

مثال 2.عند أي نقطة في الرسم البياني للوظيفة ص=س 2 + 1 تحتاج إلى رسم ظل بحيث ينقطع عن الشكل الذي يشكله الرسم البياني لهذه الوظيفة والخطوط المستقيمة ص= 0، س= 0، س= 1 شبه منحرف مع أكبر مساحة؟

حل.يترك م 0 (x 0 ، ذ 0 ) - نقطة الرسم البياني للوظيفة ص=س 2 + 1، حيث يتم رسم المماس المطلوب.

دعونا نجد معادلة الظل ص = ص 0 +و (x 0 )(س-س 0 ) .

لدينا:

لهذا

.

أوجد مساحة شبه المنحرف أوابك.

.

ب– نقطة تقاطع المماس مع الخط المستقيم س= 1 

تم اختصار المهمة إلى إيجاد أكبر قيمة للدالة

س(س)=–س 2 +x+ 1 على المقطع. سوف نجد س (س)=– 2س+ 1. أوجد النقطة الحرجة من الشرط س (س)= 0  س=.

نرى أن الدالة تصل إلى أكبر قيمة لها عند س=. سوف نجد
.

إجابة:يجب رسم المماس عند هذه النقطة
.

لاحظ أن مشكلة العثور على التكامل بناءً على معناه الهندسي غالبًا ما تتم مواجهتها. دعونا نوضح بمثال كيف يتم حل هذه المشكلة.

مثال 4.باستخدام المعنى الهندسي للتكامل، احسب

أ )
; ب)
.

حل.

أ)
– تساوي مساحة شبه منحرف منحني تحده خطوط.

ص دعونا نتحول

– النصف العلوي من الدائرة مع المركز ر(1;0) ونصف القطر ص = 1.

لهذا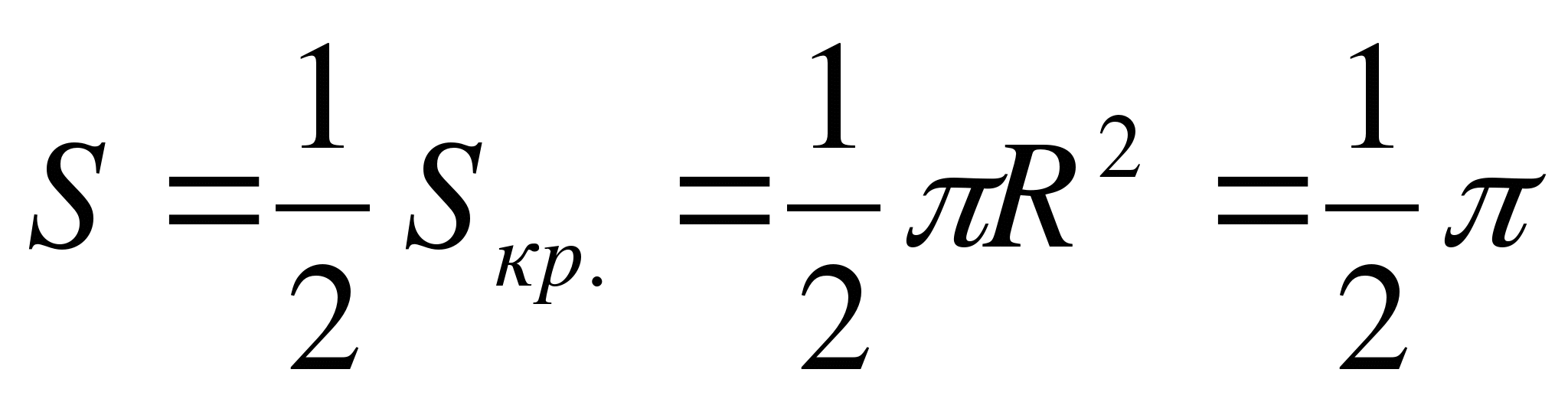
.

إجابة:
.

ب) الجدال بالمثل، دعونا نبني منطقة محدودة بالرسوم البيانية .2 – 2س+ 2، مماس لها في النقاط أ
, ب(4;2)

ص=–9س- 59، القطع المكافئ ص= 3س 2 +الفأس+ 1- إذا علم أن مماس القطع المكافئ عند النقطة س=– 2 مع المحور ثورحجم الزاوية com.arctg 6.

يجد أ، إذا علم أن مساحة شبه منحرف منحني الأضلاع تحدها خطوط ص= 3س 3 + 2س، س = أ، ص = 0 يساوي واحد.

أوجد أصغر مساحة في الشكل الذي يحده القطع المكافئ ص=س 2 + 2س- 3 ومستقيم ص=ك×+ 1.

6. مرحلة معلومات الواجب المنزلي.

الأهداف: التأكد من فهم الطلاب للغرض والمحتوى وطرق إنجاز الواجبات المنزلية رقم 18، 19،20،21 فردي

7. تلخيص الدرس.

الهدف: تقديم تقييم نوعي لعمل الفصل والطلاب الفرديين.