தனிமைப்படுத்தப்பட்ட ஒற்றை புள்ளிகள். தனிமைப்படுத்தப்பட்ட ஒற்றை புள்ளிகள், அவற்றின் வகைப்பாடு

வரையறை.செயல்பாட்டின் ஒருமைப் புள்ளி அழைக்கப்படுகிறது தனிமைப்படுத்தப்பட்ட, இந்த புள்ளியின் சில சுற்றுப்புறங்களில் ஒரு பகுப்பாய்வு செயல்பாடு இருந்தால் (அதாவது, வளையத்தில் பகுப்பாய்வு).

ஒரு செயல்பாட்டின் தனிமைப்படுத்தப்பட்ட ஒருமைப் புள்ளிகளின் வகைப்பாடு ஒரு ஒற்றைப் புள்ளியின் சுற்றுப்புறத்தில் இந்தச் செயல்பாட்டின் நடத்தையுடன் தொடர்புடையது.

வரையறை.புள்ளி அழைக்கப்படுகிறது செலவழிக்கக்கூடியது இந்தச் செயல்பாட்டின் வரையறுக்கப்பட்ட வரம்பு இல் இருந்தால், ஒரு செயல்பாட்டின் ஒற்றைப் புள்ளி.

உதாரணம் 5செயல்பாடு ஒரு புள்ளியில் நீக்கக்கூடிய தனித்தன்மையைக் கொண்டுள்ளது என்பதைக் காட்டு.

தீர்வு.முதல் குறிப்பிடத்தக்க வரம்பை நினைவுபடுத்துகிறோம், நாங்கள் கணக்கிடுகிறோம்

இதன் பொருள் கொடுக்கப்பட்ட செயல்பாடு புள்ளியில் நீக்கக்கூடிய ஒருமைப்பாட்டைக் கொண்டுள்ளது.

பணி 4.புள்ளி நீக்கக்கூடியது என்பதைக் காட்டு.

வரையறை.புள்ளி அழைக்கப்படுகிறது கம்பம் செயல்பாடு , இந்த செயல்பாடு காலவரையின்றி அதிகரித்தால் , அதாவது .

ஒரு பகுப்பாய்வு செயல்பாட்டின் பூஜ்ஜியத்திற்கும் துருவத்திற்கும் இடையிலான தொடர்பைக் கவனத்தில் கொள்வோம். செயல்பாட்டைப் பிரதிநிதித்துவப்படுத்துவோம்.

ஒரு புள்ளி ஒரு செயல்பாட்டின் எளிய பூஜ்ஜியமாக இருந்தால், செயல்பாடு ஒரு எளிய துருவத்தைக் கொண்டுள்ளது

புள்ளி என்பது செயல்பாட்டிற்கான வரிசை பூஜ்ஜியமாக இருந்தால், செயல்பாட்டிற்கு அது துருவமாகும் உத்தரவு.

எடுத்துக்காட்டு 6செயல்பாடு ஒரு புள்ளியில் மூன்றாம் வரிசை துருவத்தைக் கொண்டுள்ளது என்பதைக் காட்டு.

தீர்வு.அனுமானித்து , நாம் பெறுகிறோம் . நாம் பூஜ்ஜியத்தை நோக்கிச் செல்லும்போது, ​​எந்தச் சட்டத்தின்படியும், நம்மிடம் உள்ளது. பின்னர் , மற்றும் அதனுடன் செயல்பாடு தன்னை காலவரையின்றி அதிகரிக்கிறது. எனவே, அதாவது, ஒருமை புள்ளி ஒரு துருவமாகும். ஒரு செயல்பாட்டிற்கு, இந்த புள்ளி வெளிப்படையாக மூன்று பூஜ்ஜியமாகும். எனவே, இந்தச் செயல்பாட்டிற்கு, புள்ளி மூன்றாம் வரிசையின் துருவமாகும்.

பணி 5.புள்ளியில் ஒரு எளிய துருவம் இருப்பதைக் காட்டு.

வரையறை.புள்ளி அழைக்கப்படுகிறது அடிப்படையில் சிறப்பு செயல்பாட்டின் புள்ளி இந்த கட்டத்தில் செயல்பாட்டின் வரையறுக்கப்பட்ட அல்லது எல்லையற்ற வரம்பு இல்லை என்றால் (செயல்பாட்டின் நடத்தை வரையறுக்கப்படவில்லை).

செயல்பாட்டின் இன்றியமையாத ஒருமைப் புள்ளியாக இருக்கட்டும். பின் ஒதுக்கப்பட்ட எந்த கலப்பு எண்ணுக்கும், புள்ளிகளின் வரிசை ஒன்று வரிசையாக இருக்கும், அதனுடன் மதிப்புகள் : ( சோச்சோக்கியின் தேற்றம்).

எடுத்துக்காட்டு 7ஒரு புள்ளியில் உள்ள செயல்பாடு ஒரு அத்தியாவசிய ஒருமைப்பாட்டைக் கொண்டுள்ளது என்பதைக் காட்டுங்கள்.

தீர்வு.புள்ளியின் அருகாமையில் கொடுக்கப்பட்ட செயல்பாட்டின் நடத்தையைக் கவனியுங்கள். உண்மையான அச்சின் நேர்மறை பகுதியுடன் (அதாவது) நாம் மற்றும் ; உண்மையான அச்சின் எதிர்மறை பகுதியுடன் (அதாவது), பின்னர் மற்றும் . எனவே இதற்கு வரம்பு இல்லை. வரையறையின்படி, ஒரு செயல்பாடு ஒரு புள்ளியில் அத்தியாவசிய ஒருமைப்பாட்டைக் கொண்டுள்ளது.

சோச்சோக்கி தேற்றத்தின் பார்வையில் இருந்து பூஜ்ஜியத்தில் செயல்பாட்டின் நடத்தையை கருத்தில் கொள்வோம். பூஜ்ஜியம் மற்றும் முடிவிலி தவிர வேறு எந்த கலப்பு எண்ணாகவும் இருக்கட்டும்.

சமத்துவத்திலிருந்து நாம் காண்கிறோம். அனுமானித்து, நாம் புள்ளிகளின் வரிசையைப் பெறுகிறோம். வெளிப்படையாக, . இந்த வரிசையின் ஒவ்வொரு புள்ளியிலும், செயல்பாடு சமமாக இருக்கும், எனவே

பணி 6.செயல்பாடு ஒரு புள்ளியில் இன்றியமையாத தனித்தன்மையைக் கொண்டுள்ளது என்பதைக் காட்டு.

முடிவிலியில் ஒரு புள்ளி எப்போதும் செயல்பாட்டிற்கு சிறப்பு என்று கருதப்படுகிறது. இந்தச் சார்பு மூலத்தை மையமாகக் கொண்ட சில வட்டத்திற்கு வெளியே வேறு ஒருமைப் புள்ளிகளைக் கொண்டிருக்கவில்லை என்றால், ஒரு புள்ளி ஒரு செயல்பாட்டின் தனிமைப்படுத்தப்பட்ட ஒருமைப் புள்ளி என்று அழைக்கப்படுகிறது.

தனிமைப்படுத்தப்பட்ட ஒருமைப் புள்ளிகளின் வகைப்பாடு வழக்குக்கு நீட்டிக்கப்படலாம்.

எடுத்துக்காட்டு 8செயல்பாடு முடிவிலியில் இரட்டை துருவத்தைக் கொண்டுள்ளது என்பதைக் காட்டு.

தீர்வு.செயல்பாட்டைக் கவனியுங்கள், புள்ளியின் சுற்றுப்புறத்தில் ஒரு பகுப்பாய்வு செயல்பாடு எங்கே உள்ளது, மற்றும் . இதன் பொருள் செயல்பாடு முடிவிலியில் இரட்டை பூஜ்ஜியத்தைக் கொண்டுள்ளது, ஆனால் செயல்பாட்டிற்கு புள்ளி இரட்டை துருவமாகும்.

எடுத்துக்காட்டு 9முடிவிலியில் செயல்பாட்டிற்கு இன்றியமையாத ஒருமை இருப்பதைக் காட்டுங்கள்.

தீர்வு.இதே போன்ற பிரச்சனை pr.7 இல் கருதப்படுகிறது. எல்லையற்ற தொலைதூரப் புள்ளியின் சுற்றுப்புறத்தில் ஒரு செயல்பாட்டின் நடத்தையைக் கவனியுங்கள். உண்மையான அச்சின் நேர்மறை பகுதியிலும், உண்மையான அச்சின் எதிர்மறை பகுதியிலும். இதன் பொருள் ஒரு புள்ளியில் செயல்பாட்டின் வரம்பு இல்லை மற்றும் வரையறையின் அடிப்படையில், இந்த புள்ளி அடிப்படையில் ஒருமையாகும்.

ஒரு கட்டத்தில் ஒரு செயல்பாட்டின் ஒருமையின் தன்மையை மதிப்பிடலாம் முக்கிய பாகம் இந்த புள்ளியின் சுற்றுப்புறத்தில் லாரன்ட் விரிவாக்கம்.

தேற்றம் 1.புள்ளி இருக்க வேண்டும் செலவழிக்கக்கூடியது செயல்பாட்டின் ஒருமைப் புள்ளி , அதனுடன் தொடர்புடைய லாரன்ட் விரிவாக்கம் அவசியம் மற்றும் போதுமானது முக்கிய பகுதியைக் கொண்டிருக்கவில்லை.

பணி 6.புள்ளியின் சுற்றுப்புறத்தில் செயல்பாட்டின் டெய்லர் விரிவாக்கத்தைப் பயன்படுத்தி, அது பூஜ்ஜியத்தில் நீக்கக்கூடிய ஒருமைத்தன்மையைக் கொண்டுள்ளது என்பதைக் காட்டுங்கள்.

தேற்றம் 2.புள்ளி இருக்க வேண்டும் கம்பம் செயல்பாடுகள், அவசியம் மற்றும் போதுமானது முக்கிய பாகம் தொடர்புடைய லாரன்ட் விரிவாக்கம் வரையறுக்கப்பட்ட எண்ணிக்கையிலான உறுப்பினர்களைக் கொண்டிருந்தது :

அதிக எதிர்மறை காலத்தின் எண்ணிக்கை துருவத்தின் வரிசையை தீர்மானிக்கிறது.

இந்த வழக்கில், செயல்பாட்டை இவ்வாறு குறிப்பிடலாம்

புள்ளியில் செயல்பாடு பகுப்பாய்வு எங்கே, துருவத்தின் வரிசை.

எடுத்துக்காட்டு 10செயல்பாடு புள்ளிகளில் எளிய துருவங்களைக் கொண்டுள்ளது என்பதைக் காட்டு.

தீர்வு.ஒரு புள்ளியைக் கருத்தில் கொள்வோம். எடுத்துக்காட்டு 2 இல் பெறப்பட்ட இந்தப் புள்ளியின் அருகாமையில் இந்தச் செயல்பாட்டின் லாரன்ட் விரிவாக்கத்தைப் பயன்படுத்துகிறோம்:

இந்த விரிவாக்கத்தின் முக்கிய பகுதியில் உள்ள மிக உயர்ந்த (மற்றும் ஒரே) எதிர்மறை சக்தி ஒன்றுக்கு சமமாக இருப்பதால், புள்ளி இந்த செயல்பாட்டின் எளிய துருவமாகும்.

இந்த முடிவை வேறு வழியில் பெற்றிருக்கலாம். படிவத்தில் பிரதிநிதித்துவம் செய்வோம் மற்றும் வைப்போம் - இது புள்ளியில் பகுப்பாய்வு செய்யும் ஒரு செயல்பாடு மற்றும் . எனவே, (8) காரணமாக இந்தச் செயல்பாடு புள்ளியில் ஒரு எளிய துருவத்தைக் கொண்டுள்ளது.

மற்றொரு வழி: புள்ளியில் ஒரு எளிய பூஜ்ஜியத்தைக் கொண்ட ஒரு செயல்பாட்டைக் கருதுங்கள். எனவே, இந்த கட்டத்தில் இது ஒரு எளிய துருவத்தைக் கொண்டுள்ளது.

அதேபோல, ஃபங்ஷனைப் படிவத்தில் எழுதினால், புள்ளியில் ஒரு செயல்பாடு பகுப்பாய்வு மற்றும் , புள்ளி என்பது செயல்பாட்டின் எளிய துருவம் என்பது உடனடியாகத் தெளிவாகிறது.

பணி 7.செயல்பாடு புள்ளியில் 2 வது வரிசையின் துருவத்தையும் புள்ளியில் 4 வது வரிசையின் துருவத்தையும் கொண்டுள்ளது என்பதைக் காட்டு.

தேற்றம் 3.புள்ளி இருக்க வேண்டும் அடிப்படையில் சிறப்பு செயல்பாட்டின் புள்ளி , அது அவசியம் மற்றும் போதுமானது முக்கிய பாகம் புள்ளியின் அருகில் உள்ள லாரன்ட் விரிவாக்கம் எண்ணற்ற உறுப்பினர்களைக் கொண்டிருந்தது .

எடுத்துக்காட்டு 11.செயல்பாட்டின் புள்ளியில் ஒருமையின் தன்மையை தீர்மானிக்கவும்

தீர்வு.கொசைனின் நன்கு அறியப்பட்ட விரிவாக்கத்தில், நாங்கள் இதற்குப் பதிலாக வைக்கிறோம்:

எனவே, ஒரு புள்ளியின் சுற்றுப்புறத்தில் உள்ள லாரன்ட் விரிவாக்கம் வடிவம் கொண்டது

இங்கே சரியான பகுதி ஒரு சொல். மற்றும் முக்கிய பகுதி எண்ணற்ற சொற்களைக் கொண்டுள்ளது, எனவே புள்ளி அடிப்படையில் ஒருமையில் உள்ளது.

பணி 8.ஒரு கட்டத்தில் செயல்பாடு இன்றியமையாத தனித்தன்மையைக் கொண்டுள்ளது என்பதைக் காட்டுங்கள்.

சில செயல்பாடுகளைக் கருத்தில் கொண்டு, அதன் Laurent விரிவாக்கத்தை புள்ளியில் எழுதுங்கள்:

புள்ளி புள்ளிக்கு செல்லும் போது, ​​ஒரு மாற்றீடு செய்வோம். இப்போது, ​​முடிவிலியில் ஒரு புள்ளியின் அருகில், நம்மிடம் உள்ளது

இது ஒரு புதிய பதவியை அறிமுகப்படுத்த உள்ளது. நாம் பெறுகிறோம்

முக்கிய பகுதி எங்கே, மற்றும் எல்லையற்ற தொலைதூர புள்ளியின் சுற்றுப்புறத்தில் செயல்பாட்டின் லாரன்ட் விரிவாக்கத்தின் வழக்கமான பகுதியாகும். எனவே, ஒரு புள்ளியின் சுற்றுப்புறத்தில் உள்ள ஒரு செயல்பாட்டின் லாரன்ட் விரிவாக்கத்தில், முக்கிய பகுதி நேர்மறை சக்திகளில் ஒரு தொடராகும், அதே நேரத்தில் சரியான பகுதி எதிர்மறை சக்திகளில் ஒரு தொடராகும். இதைக் கருத்தில் கொண்டு

எவ்வாறாயினும், ஒருமைப்பாட்டின் தன்மையைத் தீர்மானிப்பதற்கான மேற்கூறிய அளவுகோல்கள் எல்லையற்ற தொலைதூரப் புள்ளிக்கு செல்லுபடியாகும்.

எடுத்துக்காட்டு 12.புள்ளியில் செயல்பாட்டின் ஒருமையின் தன்மையைக் கண்டறியவும். , பின்னர் ஒரு கட்டத்தில் அது தனிமைப்படுத்தப்படாததாக மாறலாம்.

எடுத்துக்காட்டு 15எல்லையற்ற தொலைதூர புள்ளியில் உள்ள செயல்பாடு ஒரு அத்தியாவசிய ஒருமைப்பாட்டைக் கொண்டுள்ளது. செயல்பாட்டிற்கான புள்ளி ஒரு தனிமைப்படுத்தப்பட்ட ஒரு புள்ளி அல்ல என்பதைக் காட்டு.

தீர்வு.இந்தச் செயல்பாடானது வகுப்பின் பூஜ்ஜியங்களில், அதாவது புள்ளிகளில், எண்ணற்ற துருவங்களைக் கொண்டுள்ளது. , பின்னர் புள்ளி , எந்த சுற்றுப்புறத்தில் துருவங்கள் உள்ளன , அது துருவங்களுக்கான வரம்பு புள்ளியாகும்.

இரண்டு தன்னாட்சி வேறுபட்ட சமன்பாடுகளின் அமைப்புகளால் விவரிக்கப்பட்ட மாதிரிகள்.

கட்ட விமானம். கட்ட உருவப்படம். ஐசோக்லைன் முறை. முக்கிய ஐசோக்லைன்கள். நிலையான நிலை நிலைத்தன்மை. நேரியல் அமைப்புகள். முக்கிய புள்ளி வகைகள்: முனை, சேணம், கவனம், மையம். எடுத்துக்காட்டு: முதல் வரிசை இரசாயன எதிர்வினைகள்.

உயிரியல் அமைப்புகளின் பண்புகளின் தரமான மாடலிங் பற்றிய மிகவும் சுவாரஸ்யமான முடிவுகள் இரண்டு வேறுபட்ட சமன்பாடுகளின் மாதிரிகளில் பெறப்பட்டன, அவை முறையைப் பயன்படுத்தி ஒரு தரமான ஆய்வுக்கு அனுமதிக்கின்றன. கட்ட விமானம். பொது வடிவத்தின் இரண்டு தன்னாட்சி சாதாரண வேறுபாடு சமன்பாடுகளின் அமைப்பைக் கவனியுங்கள்

(4.1)

P(x,y), Q(x,y)- தொடர்ச்சியான செயல்பாடுகள் சில டொமைனில் வரையறுக்கப்பட்டுள்ளன ஜியூக்ளிடியன் விமானம் ( x,y- கார்ட்டீசியன் ஆயத்தொலைவுகள்) மற்றும் இந்தப் பகுதியில் உள்ள வரிசையின் தொடர்ச்சியான வழித்தோன்றல்கள் முதல் விட குறைவாக இல்லை.

பிராந்தியம் ஜிவரம்பற்ற அல்லது வரையறுக்கப்பட்டதாக இருக்கலாம். மாறிகள் என்றால் x, yஒரு குறிப்பிட்ட உயிரியல் பொருள் (பொருட்களின் செறிவு, இனங்கள் மிகுதியாக), பெரும்பாலும் பகுதி ஜிவலது அரை-தளத்தின் நேர்மறை நால்வகை:

0 £ எக்ஸ்< ¥ ,0 £ ஒய்< ¥ .

பொருட்களின் செறிவு அல்லது உயிரினங்களின் மிகுதியும் மேலே இருந்து கப்பலின் அளவு அல்லது வாழ்விடத்தின் பகுதியால் வரையறுக்கப்படலாம். பின்னர் மாறிகளின் வரம்பு வடிவம் உள்ளது:

0 £ எக்ஸ்< x 0 , 0 £ ஒய்< y 0 .

மாறிகள் x, yசமன்பாடுகளின் (4.1) அமைப்புக்கு ஏற்ப நேரத்தை மாற்றவும், இதனால் அமைப்பின் ஒவ்வொரு நிலையும் மாறிகளின் மதிப்புகளின் ஜோடிக்கு ஒத்திருக்கும் ( x, y).

மாறாக, ஒவ்வொரு ஜோடி மாறிகளுக்கும் ( x, y) அமைப்பின் ஒரு குறிப்பிட்ட நிலைக்கு ஒத்துள்ளது.

மாறிகளின் மதிப்புகள் திட்டமிடப்பட்ட ஒருங்கிணைப்பு அச்சுகளைக் கொண்ட ஒரு விமானத்தைக் கவனியுங்கள். x,y. ஒவ்வொரு புள்ளியும் எம்இந்த விமானம் அமைப்பின் ஒரு குறிப்பிட்ட நிலைக்கு ஒத்துள்ளது. அத்தகைய விமானம் கட்ட விமானம் என்று அழைக்கப்படுகிறது மற்றும் அமைப்பின் அனைத்து நிலைகளின் மொத்தத்தை சித்தரிக்கிறது. M(x, y) புள்ளியை சித்தரிக்கும் அல்லது குறிக்கும் புள்ளி என்று அழைக்கப்படுகிறது.

ஆரம்ப நேரத்தில் விடுங்கள் t=t 0 புள்ளி ஒருங்கிணைப்புகளைக் குறிக்கிறது எம் 0 (எக்ஸ்(டி 0),ஒய்(டி 0)). ஒவ்வொரு அடுத்த கணத்திலும் டிமாறிகளின் மதிப்புகளில் ஏற்படும் மாற்றங்களுக்கு ஏற்ப சித்தரிக்கும் புள்ளி நகரும் எக்ஸ்(டி),ஒய்(டி). புள்ளிகளின் தொகுப்பு எம்(எக்ஸ்(டி), y(t)) கட்ட விமானத்தில், காலப்போக்கில் மாறிகளை மாற்றும் செயல்பாட்டில் அமைப்பின் நிலைகளுக்கு இது பொருந்துகிறது x(t), y(t)சமன்பாடுகளின் படி (4.1), அழைக்கப்படுகிறது கட்டப் பாதை.

மாறிகளின் வெவ்வேறு ஆரம்ப மதிப்புகளுக்கான கட்டப் பாதைகளின் தொகுப்பு கணினியின் எளிதில் காணக்கூடிய "உருவப்படத்தை" வழங்குகிறது. கட்டிடம் கட்ட உருவப்படம்மாறிகளில் ஏற்படும் மாற்றங்களின் தன்மை பற்றிய முடிவுகளை எடுக்க உங்களை அனுமதிக்கிறது x, yசமன்பாடுகளின் அசல் அமைப்பின் பகுப்பாய்வு தீர்வுகளை அறியாமல்(4.1).

ஒரு கட்ட உருவப்படத்தை சித்தரிக்க, கட்ட விமானத்தின் ஒவ்வொரு புள்ளியிலும் கணினி பாதைகளுக்கான திசைகளின் திசையன் புலத்தை உருவாக்குவது அவசியம். அதிகரிப்பைக் குறிப்பிடுவதன் மூலம்டி t>0,தொடர்புடைய அதிகரிப்புகளைப் பெறுகிறோம் டி எக்ஸ்மற்றும் டி ஒய்வெளிப்பாடுகளிலிருந்து:

டி x=P(x,y)டி டி,

டி y=Q(x,y)டி டி.

திசையன் திசை dy/dxபுள்ளியில் ( x, y) செயல்பாடுகளின் அடையாளத்தைப் பொறுத்தது P(x, y), Q(x, y)மற்றும் ஒரு அட்டவணை மூலம் கொடுக்க முடியும்:

P(x,y)>0,Q(x,y)>0
P(x,y)<0,Q(x,y)<0
P(x,y)>0,Q(x,y)<0
P(x,y)<0,Q(x,y)>0

.(4.2)

இந்த சமன்பாட்டிற்கான தீர்வு y=y(x, c), அல்லது மறைமுகமாக எஃப்(x,y)=c,எங்கே உடன்ஒருங்கிணைப்பின் மாறிலி, சமன்பாட்டின் ஒருங்கிணைந்த வளைவுகளின் குடும்பத்தை அளிக்கிறது (4.2) - கட்டப் பாதைகள்அமைப்பு (4.1) விமானத்தில் x, y.

ஐசோக்லைன் முறை

ஒரு கட்ட உருவப்படத்தை உருவாக்க, ஒருவர் பயன்படுத்துகிறார் ஐசோக்லைன் முறை -ஒரு குறிப்பிட்ட கோணத்தில் ஒருங்கிணைந்த வளைவுகளை வெட்டும் கட்டத் தளத்தில் கோடுகள் வரையப்படுகின்றன. ஐசோக்லைன் சமன்பாடு (4.2) இலிருந்து பெறுவது எளிது. போடுவோம்

எங்கே ஆனால்– ஒரு குறிப்பிட்ட நிலையானது. பொருள் ஆனால்கட்டப் பாதைக்கு தொடுகோடு சாய்வின் தொடுகோட்டைக் குறிக்கிறது மற்றும் இதிலிருந்து மதிப்புகளை எடுக்கலாம் -¥ க்கு + ¥ . பதிலாக பதிலாக dy/dx(4.2) அளவு ஆனால்ஐசோக்லைன் சமன்பாட்டைப் பெறுகிறோம்:

.(4.3)

சமன்பாடு (4.3) விமானத்தின் ஒவ்வொரு புள்ளியிலும் உள்ள புள்ளியைத் தவிர, தொடர்புடைய ஒருங்கிணைந்த வளைவுக்கான ஒரே தொடுகோடு தீர்மானிக்கிறது பி(x,y)= 0, கே (x,y) = 0 , இதில் டேன்ஜென்ட்டின் திசை காலவரையற்றதாக மாறும், ஏனெனில் வழித்தோன்றலின் மதிப்பு காலவரையற்றதாக மாறும்:

.

இந்த புள்ளி அனைத்து ஐசோக்லைன்களின் வெட்டும் புள்ளியாகும் - சிறப்பு புள்ளி.இது ஒரே நேரத்தில் மாறிகளின் நேர வழித்தோன்றல்களை அழிக்கிறது எக்ஸ்மற்றும் ஒய்.

எனவே, ஒருமைப் புள்ளியில், மாறிகளின் மாற்ற விகிதங்கள் பூஜ்ஜியத்திற்கு சமமாக இருக்கும். எனவே, கட்டப் பாதைகளின் வேறுபட்ட சமன்பாடுகளின் ஒருமைப் புள்ளி (4.2) ஒத்துள்ளது அமைப்பின் நிலையான நிலை(4.1), மற்றும் அதன் ஆயத்தொலைவுகள் மாறிகளின் நிலையான மதிப்புகள் x, y.

குறிப்பாக ஆர்வமாக உள்ளன முக்கிய ஐசோக்லைன்கள்:

dy/dx=0, P(x,y)=0 – கிடைமட்ட தொடுகோடுகளின் ஐசோக்லைன் மற்றும்

dy/dx=¥ , கே(x,y)=0 – செங்குத்து தொடுகோடுகளின் ஐசோக்லைன்.

முக்கிய ஐசோக்லைன்களை உருவாக்கி, அவற்றின் குறுக்குவெட்டு புள்ளியைக் கண்டறிவதன் மூலம் (x,y), நிபந்தனைகளை பூர்த்தி செய்யும் ஆயங்கள்:

கட்டத் தளத்தின் அனைத்து ஐசோக்லைன்களின் குறுக்குவெட்டுப் புள்ளியைக் கண்டுபிடிப்போம், இதில் கட்டப் பாதைகளுக்கான தொடுகோடுகளின் திசை காலவரையின்றி இருக்கும். இது - ஒருமை புள்ளி, இது ஒத்துள்ளது அமைப்பின் நிலையான நிலை(படம் 4.2).

கணினி (4.1) கட்டத் தளத்தில் உள்ள முக்கிய ஐசோக்லைன்களின் குறுக்குவெட்டுப் புள்ளிகளைப் போலவே பல நிலையான நிலைகளைக் கொண்டுள்ளது.

ஒவ்வொரு கட்டப் பாதையும் ஒரே நிலைகளைக் கடந்து செல்லும் ஒரு இயக்கவியல் அமைப்பின் இயக்கங்களின் தொகுப்பிற்கு ஒத்திருக்கிறது மற்றும் நேரக் குறிப்பின் தொடக்கத்தில் மட்டுமே ஒருவருக்கொருவர் வேறுபடுகிறது.

கௌச்சி தேற்றத்தின் நிபந்தனைகள் பூர்த்தி செய்யப்பட்டால், ஒவ்வொரு இடத்தின் ஒவ்வொரு புள்ளியிலும் x, y, tஒரு ஒருங்கிணைந்த வளைவு வழியாக செல்கிறது. அதே உண்மை, சுயாட்சிக்கு நன்றி, கட்டப் பாதைகளுக்கு: ஒரு தனித்துவமான கட்டப் பாதை கட்ட விமானத்தின் ஒவ்வொரு புள்ளியிலும் செல்கிறது.

நிலையான நிலை நிலைத்தன்மை

அமைப்பு சமநிலையில் இருக்கட்டும்.

பின்னர் பிரதிநிதித்துவ புள்ளி அமைப்பின் ஒற்றை புள்ளிகளில் ஒன்றில் அமைந்துள்ளது, இதில், வரையறையின்படி:

.

ஒரு ஒற்றைப் புள்ளி நிலையானதா இல்லையா என்பது, பிரதிநிதிப் புள்ளி நிலையான நிலையில் இருந்து சிறிய விலகலுடன் வெளியேறுகிறதா இல்லையா என்பதன் மூலம் தீர்மானிக்கப்படுகிறது. இரண்டு சமன்பாடுகளின் அமைப்பிற்குப் பயன்படுத்தப்படும், மொழியின் நிலைத்தன்மையின் வரையறைஇ, ஈபின்வருமாறு.

சமநிலை நிலையிலிருந்து விலகல்கள் ஏதேனும் கொடுக்கப்பட்டால் சமநிலை நிலை நிலையானது (இ )பகுதியை குறிப்பிடலாம் ஈ (இ ), சமநிலை நிலையைச் சுற்றியுள்ளது மற்றும் பிராந்தியத்திற்குள் தொடங்கும் எந்தப் பாதையும் இல்லாத சொத்து உள்ளது ஈ , எல்லையை அடையவே முடியாது இ . (படம் 4.4)

ஒரு பெரிய வகை அமைப்புகளுக்கு - கடினமான அமைப்புகள் – சமன்பாடுகளின் வகைகளில் ஒரு சிறிய மாற்றத்துடன் மாறாத நடத்தையின் தன்மை, நிலையான நிலைக்கு அருகிலுள்ள நடத்தை வகை பற்றிய தகவல்களை அசல் அல்ல, ஆனால் எளிமைப்படுத்தப்பட்டதைப் படிப்பதன் மூலம் பெறலாம். நேர்கோட்டானதுஅமைப்பு.

நேரியல் அமைப்புகள்.

இரண்டு நேரியல் சமன்பாடுகளின் அமைப்பைக் கவனியுங்கள்:

.(4.4)

இங்கே ஏ பி சி டி- மாறிலிகள், x, y- கட்ட விமானத்தில் கார்ட்டீசியன் ஒருங்கிணைப்புகள்.

பொதுவான தீர்வு வடிவத்தில் தேடப்படும்:

.(4.5)

இந்த வெளிப்பாடுகளை (4.4) இல் மாற்றவும் மற்றும் குறைக்கவும் இ எல் டி:

(4.6)

அறியப்படாத சமன்பாடுகளின் இயற்கணித அமைப்பு (4.6). ஏ, பிதெரியாதவற்றின் குணகங்களால் ஆன அதன் நிர்ணயம் பூஜ்ஜியத்திற்கு சமமாக இருந்தால் மட்டுமே பூஜ்ஜியமற்ற தீர்வு உள்ளது:

.

இந்த தீர்மானத்தை விரிவாக்குவதன் மூலம், அமைப்பின் சிறப்பியல்பு சமன்பாட்டைப் பெறுகிறோம்:

.(4.7)

இந்த சமன்பாட்டின் தீர்வு காட்டி மதிப்புகளை வழங்குகிறதுஎல் 1,2 , இதன் கீழ் பூஜ்ஜியமற்ற மதிப்புகள் சாத்தியமாகும் ஏமற்றும் பிசமன்பாட்டின் தீர்வுகள் (4.6). இந்த மதிப்புகள்

.(4.8)

தீவிர வெளிப்பாடு எதிர்மறையாக இருந்தால், பின்னர்எல் 1,2 சிக்கலான இணை எண்கள். சமன்பாட்டின் இரண்டு வேர்களும் (4.7) பூஜ்ஜியமற்ற உண்மையான பகுதிகளைக் கொண்டுள்ளன மற்றும் பல வேர்கள் இல்லை என்று வைத்துக்கொள்வோம். பின்னர் அமைப்பின் பொதுவான தீர்வு (4.4) அடுக்குகளுடன் கூடிய அடுக்குகளின் நேரியல் கலவையாக குறிப்பிடப்படலாம்.எல் 1 , எல் 2 :

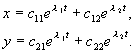(4.9)

கட்ட விமானத்தில் அமைப்பின் சாத்தியமான பாதைகளின் தன்மையை பகுப்பாய்வு செய்ய, நாங்கள் பயன்படுத்துகிறோம் நேரியல் ஒரே மாதிரியான ஒருங்கிணைப்பு மாற்றம்,அமைப்பை கொண்டு வரும் நியமன வடிவம்:

,(4.10)

இது அசல் அமைப்புடன் (4.4) ஒப்பிடும்போது கட்ட விமானத்தில் மிகவும் வசதியான பிரதிநிதித்துவத்தை அனுமதிக்கிறது. புதிய ஆயங்களை அறிமுகப்படுத்துவோம்ξ , η சூத்திரங்களின்படி:

(4.1)

உண்மையான பகுதிகள் பூஜ்ஜியத்திற்கு சமமாக இல்லாவிட்டால், நேரியல் இயற்கணிதத்தின் போக்கில் இருந்து அறியப்படுகிறதுஎல் 1 , எல் 2 மாற்றங்களின் உதவியுடன் அசல் அமைப்பு (4.4) (4.11) எப்போதும் நியமன வடிவத்திற்கு (4.10) மாற்றப்படலாம் மற்றும் கட்ட விமானத்தில் அதன் நடத்தையை ஆய்வு செய்யலாம்.ξ , η . இங்கு முன்வைக்கக்கூடிய பல்வேறு வழக்குகளைக் கவனியுங்கள்.

வேர்கள் λ 1 , λ 2 - செல்லுபடியாகும் மற்றும் அதே அடையாளம்

இந்த வழக்கில், உருமாற்ற குணகங்கள் உண்மையானவை, நாங்கள் உண்மையான விமானத்திலிருந்து நகர்கிறோம்x,yஉண்மையான விமானத்திற்கு ξ, η. சமன்பாடுகளின் இரண்டாவது (4.10) ஐ முதலில் வகுத்தால், நாம் பெறுகிறோம்:

.(4.12)

இந்த சமன்பாட்டை ஒருங்கிணைத்து, நாம் கண்டுபிடிக்கிறோம்:

எங்கே .(4.13)

λ மூலம் புரிந்து கொள்ள ஒப்புக்கொள்வோம் 2 ஒரு பெரிய மாடுலஸ் கொண்ட சிறப்பியல்பு சமன்பாட்டின் வேர், இது நமது பகுத்தறிவின் பொதுவான தன்மையை மீறுவதில்லை. பின்னர், கருத்தில் உள்ள வழக்கில் வேர்கள் λ 1 , λ2 - செல்லுபடியாகும் மற்றும் அதே அடையாளம்,அ>1 , மற்றும் பரவளைய வகையின் ஒருங்கிணைந்த வளைவுகளைக் கையாளுகிறோம்.

அனைத்து ஒருங்கிணைந்த வளைவுகள் (அச்சு தவிர η , இது ஒத்துள்ளது ) அச்சின் தோற்றத்தில் தொடுதல் ξ, இது சமன்பாட்டின் ஒருங்கிணைந்த வளைவாகும் (4.11). ஆயங்களின் தோற்றம் ஒரு ஒற்றைப் புள்ளி.

கட்டப் பாதைகளில் பிரதிநிதி புள்ளியின் இயக்கத்தின் திசையை இப்போது கண்டுபிடிப்போம். λ என்றால் 1, λ 2 எதிர்மறையானவை, சமன்பாடுகள் (4.10), |ξ|, |η| காலப்போக்கில் குறைகிறது. குறிக்கும் புள்ளி தோற்றத்தை நெருங்குகிறது, ஆனால் அதை அடையவே இல்லை. இல்லையெனில், இது கௌச்சியின் தேற்றத்திற்கு முரணாக இருக்கும், இது கட்டத் தளத்தின் ஒவ்வொரு புள்ளியிலும் ஒரு கட்டப் பாதை மட்டுமே செல்கிறது என்று கூறுகிறது.

பரவளையங்களின் குடும்பத்தைப் போலவே ஒருங்கிணைந்த வளைவுகள் கடந்து செல்லும் ஒரு ஒற்றைப் புள்ளி தோற்றம் வழியாக செல்கிறது, ஒரு முனை என்று அழைக்கப்படுகிறது (படம். 4.5)

λ இல் முடிச்சு வகை சமநிலை நிலை 1, λ 2 < 0 லியாபுனோவின் கூற்றுப்படி நிலையானது, ஏனெனில் குறிக்கும் புள்ளி அனைத்து ஒருங்கிணைந்த வளைவுகளிலும் ஒருங்கிணைப்புகளின் தோற்றத்தை நோக்கி நகர்கிறது. அது நிலையான முடிச்சு. λ என்றால் 1, λ 2 > 0, பின்னர் |ξ|, |η| காலப்போக்கில் அதிகரிக்கும் மற்றும் பிரதிநிதி புள்ளி தோற்றத்திலிருந்து விலகிச் செல்கிறது. இந்த வழக்கில், ஒருமை புள்ளி– நிலையற்ற முடிச்சு .

கட்ட விமானத்தில் x, y ஒருங்கிணைந்த வளைவுகளின் நடத்தையின் பொதுவான தரமான தன்மை இருக்கும், ஆனால் ஒருங்கிணைந்த வளைவுகளுக்கான தொடுகோடுகள் ஒருங்கிணைப்பு அச்சுகளுடன் ஒத்துப்போவதில்லை. இந்த தொடுகோடுகளின் சாய்வின் கோணம் குணகங்களின் விகிதத்தால் தீர்மானிக்கப்படும் α , β , γ , δ சமன்பாடுகளில் (4.11).

வேர்கள் λ 1 , λ 2 செல்லுபடியாகும் மற்றும் வெவ்வேறு அடையாளங்கள் உள்ளன.

இருந்து மாற்றுஒருங்கிணைப்புகள் x,y ஒருங்கிணைப்புகளுக்கு ξ, η மீண்டும் உண்மையான. நியமன மாறிகளுக்கான சமன்பாடுகள் மீண்டும் வடிவத்தைக் கொண்டுள்ளன (4.10), ஆனால் இப்போது அறிகுறிகள் λ 1, λ 2 வெவ்வேறு. கட்டப் பாதை சமன்பாடு வடிவம் கொண்டது:

எங்கே , (4.14)

ஒருங்கிணைத்தல் (4.14), நாம் கண்டுபிடிக்கிறோம்

(4.15)

அது சமன்பாடு ஹைபர்போலிக் வகையின் வளைவுகளின் குடும்பத்தை வரையறுக்கிறது, இதில் இரண்டும் அச்சுகளை ஒருங்கிணைக்கிறதுஅறிகுறிகளாகும் (at அ=1 எங்களிடம் ஐசோசெல்ஸ் ஹைபர்போலாஸ் குடும்பம் இருக்கும்). இந்த வழக்கில் ஒருங்கிணைப்பு அச்சுகளும் ஒருங்கிணைந்த வளைவுகளாகும்– இவை மூலத்தின் வழியாக செல்லும் ஒரே ஒருங்கிணைந்த வளைவுகளாக இருக்கும். ஒவ்வொன்றும்இதில் மூன்று கட்டப் பாதைகள் உள்ளன: சமநிலை நிலையை நோக்கி (அல்லது சமநிலை நிலையில் இருந்து விலகி) மற்றும் சமநிலை நிலையில் இருந்து இரண்டு இயக்கங்கள். மற்ற அனைத்து ஒருங்கிணைந்த வளைவுகள்– தோற்றம் வழியாக செல்லாத ஹைபர்போலாக்கள் (படம். 4.6) இந்த ஒற்றைப் புள்ளி அழைக்கப்படுகிறது "சேணம் ». மலைச் சேணத்தின் அருகே உள்ள நிலைக் கோடுகள் சேணத்தின் அருகில் உள்ள கட்டப் பாதைகளைப் போல செயல்படுகின்றன.

சமநிலை நிலைக்கு அருகிலுள்ள கட்டப் பாதைகளில் பிரதிநிதி புள்ளியின் இயக்கத்தின் தன்மையைக் கருத்தில் கொள்வோம். உதாரணமாக, விடுங்கள்λ 1 >0 , λ 2<0 . பின்னர் அச்சில் வைக்கப்பட்ட பிரதிநிதி புள்ளி ξ , தோற்றத்திலிருந்து விலகி, அச்சில் வைக்கப்படும் η – ஆயத்தொலைவுகளின் தோற்றத்தை காலவரையின்றி அணுகும், வரையறுக்கப்பட்ட நேரத்தில் அதை அடையாமல். குறிக்கும் புள்ளி ஆரம்ப தருணத்தில் எங்கிருந்தாலும் (ஒருமைப் புள்ளி மற்றும் அறிகுறியின் புள்ளிகளைத் தவிர η =0), தொடக்கத்தில் அது ஒருங்கிணைந்த வளைவுகளில் ஒன்றில் ஒரு ஒற்றைப் புள்ளியை நோக்கி நகர்ந்தாலும், அது இறுதியில் சமநிலை நிலையில் இருந்து விலகிச் செல்லும்..

என்பது வெளிப்படையானது சேணம்-வகை ஒருமை புள்ளி எப்போதும் நிலையற்றது . அசிம்டோட்டில் சிறப்பாகத் தேர்ந்தெடுக்கப்பட்ட ஆரம்ப நிலைமைகளின் கீழ் மட்டுமேη =0 அமைப்பு சமநிலை நிலையை அணுகும். இருப்பினும், அமைப்பு நிலையற்றது என்ற கூற்றுக்கு இது முரணாக இல்லை. நீங்கள் எண்ணினால், கட்ட விமானத்தில் அமைப்பின் அனைத்து ஆரம்ப நிலைகளும் சமமாக சாத்தியமாகும், பின்னர் திசையில் இயக்கத்திற்கு ஒத்திருக்கும் அத்தகைய ஆரம்ப நிலையின் நிகழ்தகவுசெய்ய ஒருமை புள்ளி பூஜ்ஜியத்திற்கு சமம். எனவே, எந்த உண்மையான இயக்கமும் அமைப்பை சமநிலை நிலையில் இருந்து அகற்றும்.ஒருங்கிணைப்புகளுக்குத் திரும்புகிறேன்x,y,தோற்றத்தைச் சுற்றியுள்ள பாதைகளின் இயக்கத்தின் தன்மையின் அதே தரமான படத்தைப் பெறுகிறோம்.

ஒரு கணு மற்றும் சேணத்தின் கருதப்படும் நிகழ்வுகளுக்கு இடையிலான எல்லையானது வழக்குஎப்பொழுது சிறப்பியல்பு குறிகாட்டிகளில் ஒன்று, எடுத்துக்காட்டாக λ 1 , மறைந்துவிடும், இது அமைப்பின் நிர்ணயம் செய்யும் போது நிகழ்கிறது- வெளிப்பாடு adbc=0(சூத்திரம் 4.8 ஐப் பார்க்கவும் ). இந்த வழக்கில், சமன்பாடுகளின் வலது பக்கங்களின் குணகங்கள் (4.4) ஒன்றுக்கொன்று விகிதாசாரமாக இருக்கும்:

மற்றும் அமைப்பு அதன் சமநிலைக்கு கோட்டின் அனைத்து புள்ளிகளையும் கொண்டுள்ளது:

மீதமுள்ள ஒருங்கிணைந்த வளைவுகள் ஒரு சாய்வுடன் இணையான கோடுகளின் குடும்பமாகும் , λ பண்புச் சமன்பாட்டின் இரண்டாவது மூலத்தின் அடையாளத்தைப் பொறுத்து, பிரதிநிதி புள்ளிகள் சமநிலை நிலையை அணுகுகின்றன அல்லது அதிலிருந்து விலகிச் செல்கின்றன. 2 = a+d.(படம்.4. 7 ) இந்த வழக்கில், சமநிலை நிலையின் ஆயங்கள் மாறிகளின் ஆரம்ப மதிப்பைப் பொறுத்தது.

வேர்கள் λ 1 , λ 2 – சிக்கலானஇணை

இந்த வழக்கில், உண்மையில்எக்ஸ்மற்றும் ஒய்நாங்கள் செய்வோம் சிக்கலான இணைப்புகள் உள்ளன ξ , η (4.10) . இருப்பினும், இன்னும் ஒரு இடைநிலை உருமாற்றத்தை அறிமுகப்படுத்துவதன் மூலம், உண்மையான நேரியல் ஒரே மாதிரியான மாற்றத்தைக் கருத்தில் கொள்வது இந்த விஷயத்தில் சாத்தியமாகும். போடுவோம்:

(4.16)

எங்கே a, b,மற்றும் u, v – உண்மையான மதிப்புகள். இருந்து மாற்றம் என்று காட்டலாம்x,yசெய்ய u, v என்பது, எங்கள் அனுமானங்களின்படி, உண்மையான, நேரியல், பூஜ்ஜியம் அல்லாத தீர்மானிப்புடன் ஒரே மாதிரியானது. சமன்பாடுகள் காரணமாக(4.10, 4.16) எங்களிடம் உள்ளது:

எங்கே

(4.17)

சமன்பாடுகளில் இரண்டாவதாக முதலில் வகுத்தல், நாங்கள் பெறுகிறோம்:

ஒருங்கிணைக்க எளிதானது, நாம் துருவ ஒருங்கிணைப்பு அமைப்புக்கு மாறினால் (ஆர், φ ) . மாற்றுக்குப் பிறகுநாங்கள் எங்கிருந்து பெறுகிறோம்:

.(4.18)

இவ்வாறு, கட்ட விமானத்தில்u, vமடக்கைச் சுழல்களின் குடும்பத்துடன் நாங்கள் கையாள்கிறோம், அவை ஒவ்வொன்றும் உள்ளனதோற்றத்தில் அறிகுறியற்ற புள்ளி.சுருள் வடிவத்தைக் கொண்ட அனைத்து ஒருங்கிணைந்த வளைவுகளின் அறிகுறியற்ற புள்ளியாக இருக்கும் ஒருமைப் புள்ளி, உள்ளுறை நண்பர்நண்பர், அழைத்தார் கவனம் ( படம்.4.8 ) .

கட்டப் பாதைகளில் குறிக்கும் புள்ளியின் இயக்கத்தின் தன்மையைக் கருத்தில் கொள்வோம். முதல் சமன்பாடுகளை (4.17) ஆல் பெருக்குதல்u, மற்றும் இரண்டாவது vமற்றும் சேர்ப்பது, நாம் பெறுகிறோம்:

எங்கே

விடுங்கள் அ 1 < 0 (அ 1 = ரெλ ) . குறிக்கும் புள்ளி பின்னர் ஒரு வரையறுக்கப்பட்ட நேரத்தில் அதை அடையாமல் தொடர்ந்து தோற்றத்தை நெருங்குகிறது. இதன் பொருள், கட்டப் பாதைகள் முறுக்கு சுருள்கள் மற்றும் ஈரமான அலைவுகளுக்கு ஒத்திருக்கும்மாறிகள். இது - நிலையான கவனம் .

ஒரு நிலையான ஃபோகஸ் விஷயத்தில், ஒரு நிலையான முனையைப் போலவே, லியாபுனோவ் நிபந்தனை திருப்தி அடைவது மட்டுமல்லாமல், மிகவும் கடுமையான தேவையும் கூட. அதாவது, ஏதேனும் ஆரம்ப விலகல்களுக்கு, அமைப்பு இறுதியில் சமநிலை நிலைக்கு விரும்பியபடி திரும்பும். அத்தகைய நிலைத்தன்மை, இதில் ஆரம்ப விலகல்கள் அதிகரிப்பது மட்டுமல்லாமல், சிதைவு, பூஜ்ஜியமாக இருக்கும், அழைக்கப்படுகிறது முழுமையான நிலைத்தன்மை .

சூத்திரத்தில் இருந்தால் (4.18) அ 1 >0 , பின்னர் குறிக்கும் புள்ளி தோற்றத்திலிருந்து நகர்கிறது, மேலும் நாங்கள் கையாளுகிறோம் நிலையற்ற கவனம் . ஒரு விமானத்தில் இருந்து நகரும் போதுu, vகட்ட விமானத்திற்குஎக்ஸ், ஒய்சுருள்கள் சுருள்களாக இருக்கும், ஆனால் சிதைந்துவிடும்.

எப்போது என்பதை இப்போது கவனியுங்கள்அ 1 =0 . விமானத்தில் கட்டப் பாதைகள்u, vவட்டங்கள் இருக்கும் விமானத்தில் எதுx,yபொருத்தமான நீள்வட்டங்கள்:

இவ்வாறு, மணிக்குஒரு 1=0 ஒரு சிறப்பு புள்ளி மூலம்x= 0,y= 0 ஒருங்கிணைந்த வளைவு இல்லை. ஒருங்கிணைந்த வளைவுகள் மூடிய வளைவுகள், குறிப்பாக, நீள்வட்டங்கள் ஒன்றுக்கொன்று உட்பொதிக்கப்பட்டு ஒருமை புள்ளியை உள்ளடக்கியிருக்கும் அத்தகைய தனிமைப்படுத்தப்பட்ட ஒருமைப் புள்ளி, மையம் என்று அழைக்கப்படுகிறது.

இவ்வாறு, பண்புச் சமன்பாட்டின் (4.7) வேர்களின் தன்மையைப் பொறுத்து ஆறு வகையான சமநிலை சாத்தியமாகும். விமானத்தில் கட்டப் பாதைகளின் காட்சி x, yஇந்த ஆறு நிகழ்வுகளுக்கு படம் காட்டப்பட்டுள்ளது. 4.9

அரிசி. 4.9நேரியல் சமன்பாடுகளின் (4.4) அமைப்பிற்கான நிலையான நிலையின் சுற்றுப்புறத்தில் உள்ள கட்ட உருவப்படங்களின் வகைகள்.

ஐந்து வகையான சமநிலை நிலைகள் கடினமானவை, சமன்பாடுகளின் வலது பக்கங்களில் (4.4) போதுமான சிறிய மாற்றங்களுடன் அவற்றின் இயல்பு மாறாது. இந்த வழக்கில், மாற்றங்கள் வலது பக்கங்களில் மட்டும் சிறியதாக இருக்க வேண்டும், ஆனால் அவற்றின் முதல் வரிசை வழித்தோன்றல்களிலும் இருக்க வேண்டும். சமநிலையின் ஆறாவது நிலை - மையம் - கரடுமுரடானது அல்ல. சமன்பாடுகளின் வலது பக்க அளவுருக்களில் சிறிய மாற்றங்களுடன், அது ஒரு நிலையான அல்லது நிலையற்ற கவனம் செலுத்துகிறது.

பிளவுபடம் வரைபடம்

குறியீட்டை அறிமுகப்படுத்துவோம்:

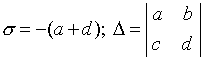. (4.11)

பின்னர் சிறப்பியல்பு சமன்பாட்டை வடிவத்தில் எழுதலாம்:

. (4.12)

செவ்வக கார்ட்டீசியன் ஆயத்தொலைவுகளைக் கொண்ட விமானத்தைக் கவனியுங்கள் கள் , டி ஒன்று அல்லது மற்றொரு வகை சமநிலை நிலைக்கு தொடர்புடைய பகுதிகளைக் குறிக்கவும், இது சிறப்பியல்பு சமன்பாட்டின் வேர்களின் தன்மையால் தீர்மானிக்கப்படுகிறது.

.(4.13)

சமநிலை நிலையின் நிலைத்தன்மைக்கான நிபந்தனை y இன் எதிர்மறை உண்மையான பகுதியின் இருப்பு ஆகும்.எல் 1 மற்றும் எல் 2 . இதற்கு தேவையான மற்றும் போதுமான நிபந்தனை ஏற்றத்தாழ்வுகளை பூர்த்தி செய்வதாகும்கள் > 0, டி > 0 . வரைபடத்தில் (4.15), இந்த நிலை அளவுரு விமானத்தின் முதல் காலாண்டில் அமைந்துள்ள புள்ளிகளுக்கு ஒத்திருக்கிறது. ஒருமை புள்ளி என்றால் கவனம் இருக்கும்எல் 1 மற்றும் எல் 2 சிக்கலான. இந்த நிலை விமானத்தின் அந்த புள்ளிகளுக்கு ஒத்திருக்கிறது , அந்த. ஒரு பரவளையத்தின் இரண்டு கிளைகளுக்கு இடையே உள்ள புள்ளிகள்கள் 2 = 4 டி. செமியாக்சிஸ் புள்ளிகள் கள் = 0, டி>0, மைய வகையின் சமநிலை நிலைகளுக்கு ஒத்திருக்கும். அதேபோல்,எல் 1 மற்றும் எல் 2 - செல்லுபடியாகும், ஆனால் வெவ்வேறு அறிகுறிகள், அதாவது. ஒரு ஒற்றை புள்ளி என்றால் சேணமாக இருக்கும் டி<0, முதலியன இதன் விளைவாக, அளவுரு விமானத்தின் பகிர்வு வரைபடத்தைப் பெறுகிறோம் கள், டி, பல்வேறு வகையான சமநிலை நிலைகளுடன் தொடர்புடைய பகுதிகளில்.

அரிசி. 4.10.பிளவுபடம் வரைபடம்

நேரியல் சமன்பாடுகளின் அமைப்புக்கு 4.4

நேரியல் அமைப்பின் குணகங்கள் என்றால் ஏ பி சி டிசில அளவுருவைப் பொறுத்து, இந்த அளவுரு மாற்றப்படும்போது, ​​மதிப்புகளும் மாறும்கள் , டி . எல்லைகளை கடந்து செல்லும் போது, ​​கட்ட உருவப்படத்தின் தன்மை தரமான முறையில் மாறுகிறது. எனவே, அத்தகைய எல்லைகள் பிளவு எல்லைகள் என்று அழைக்கப்படுகின்றன - எல்லையின் எதிர் பக்கங்களில், அமைப்பு இரண்டு இடவியல் ரீதியாக வேறுபட்ட கட்ட உருவப்படங்களைக் கொண்டுள்ளது, அதன்படி, இரண்டு வெவ்வேறு வகையான நடத்தை.

அத்தகைய மாற்றங்கள் எவ்வாறு நிகழலாம் என்பதை வரைபடம் காட்டுகிறது. சிறப்பு நிகழ்வுகளை - ஆயத்தொலைவுகளின் தோற்றம் - நாம் விலக்கினால், சேணம் y- அச்சைக் கடக்கும்போது ஒரு முனை, நிலையான அல்லது நிலையற்றதாகச் செல்ல முடியும் என்பதைக் காண்பது எளிது. ஒரு நிலையான கணு சேணம் அல்லது ஒரு நிலையான கவனம், மற்றும் பல. நிலையான முனை-நிலையான ஃபோகஸ் மற்றும் நிலையற்ற முனை-நிலையற்ற ஃபோகஸ் மாற்றங்கள் இரண்டாகப் பிரிக்கப்படுவதில்லை, ஏனெனில் கட்ட இடத்தின் இடவியல் இந்த விஷயத்தில் மாறாது. விரிவுரை 6 இல் கட்ட இடத்தின் இடவியல் மற்றும் பிளவு மாற்றங்கள் பற்றி மேலும் விரிவாகப் பேசுவோம்.

பிளவு மாற்றங்களின் கீழ், ஒருமை புள்ளியின் நிலைத்தன்மையின் தன்மை மாறுகிறது. எடுத்துக்காட்டாக, மையத்தின் மூலம் ஒரு நிலையான கவனம் நிலையற்ற மையமாக மாறும். இந்த பிளவு அழைக்கப்படுகிறது ஆண்ட்ரோனோவ்-ஹாப் பிளவுஅதை ஆய்வு செய்த விஞ்ஞானிகளின் பெயர்களால். நேரியல் அல்லாத அமைப்புகளில் இந்த பிளவு மூலம், ஒரு வரம்பு சுழற்சி பிறக்கிறது, மேலும் அமைப்பு சுய-ஊசலாடுகிறது (விரிவுரை 8 ஐப் பார்க்கவும்).

உதாரணமாக. நேரியல் இரசாயன எதிர்வினைகளின் அமைப்பு

பொருள் எக்ஸ்வெளியில் இருந்து ஒரு நிலையான விகிதத்தில் பாய்கிறது, பொருள் Y ஆக மாறும் மற்றும் பொருளின் செறிவுக்கு விகிதாசார விகிதத்தில் ஒய், எதிர்வினைக் கோளத்திலிருந்து வெளியே எடுக்கப்படுகிறது. பூஜ்ஜிய வரிசையைக் கொண்ட வெளியில் இருந்து வரும் பொருளின் வருகையைத் தவிர, அனைத்து எதிர்வினைகளும் முதல் வரிசையில் உள்ளன. எதிர்வினை திட்டம் இதுபோல் தெரிகிறது:

(4.14)

மற்றும் சமன்பாடுகளின் அமைப்பால் விவரிக்கப்படுகிறது:

(4.15)

வலது பக்கங்களை பூஜ்ஜியத்திற்கு சமன் செய்வதன் மூலம் நிலையான செறிவுகளைப் பெறுகிறோம்:

.(4.16)

அமைப்பின் கட்ட உருவப்படத்தைக் கவனியுங்கள். கணினியின் இரண்டாவது சமன்பாட்டை (4.16) முதல் ஒன்றால் வகுக்கலாம். நாங்கள் பெறுகிறோம்:

.(4.17)

சமன்பாடு (4.17) கட்ட விமானத்தில் மாறிகளின் நடத்தையை தீர்மானிக்கிறது. இந்த அமைப்பின் ஒரு கட்ட உருவப்படத்தை உருவாக்குவோம். முதலில், கட்ட விமானத்தில் முக்கிய ஐசோக்லைன்களை வரைகிறோம். செங்குத்து தொடுகோடுகளின் ஐசோக்லைனின் சமன்பாடு:

கிடைமட்ட தொடுகோடுகளின் ஐசோக்லைன் சமன்பாடு:

ஒருமை புள்ளி (நிலையான நிலை) முதன்மை ஐசோக்லைன்களின் குறுக்குவெட்டில் உள்ளது.

ஒருங்கிணைப்பு அச்சுகள் ஒருங்கிணைந்த வளைவுகளை எந்த கோணத்தில் வெட்டுகின்றன என்பதை இப்போது தீர்மானிப்போம்.

ஒரு என்றால் x= 0, பின்னர்.

இவ்வாறு, ஒருங்கிணைந்த வளைவுகளுக்கு தொடுகோடு சாய்வின் தொடுகோடு y=y(x), y அச்சைக் கடக்கிறது x=0, மேல் அரை-தளத்தில் எதிர்மறையாக உள்ளது (மாறிகள் என்பதை நினைவில் கொள்க x, yசெறிவு மதிப்புகள் உள்ளன, எனவே நாங்கள் கட்ட விமானத்தின் மேல் வலதுபுறத்தில் மட்டுமே ஆர்வமாக உள்ளோம்). இந்த வழக்கில், தொடுகோடு சாய்வின் கோணத்தின் தொடுகோட்டின் மதிப்பு தோற்றத்திலிருந்து தூரத்துடன் அதிகரிக்கிறது.

அச்சைக் கவனியுங்கள் y= 0. இந்த அச்சின் குறுக்குவெட்டில், ஒருங்கிணைந்த வளைவுகள் சமன்பாட்டால் விவரிக்கப்படுகின்றன

மணிக்கு abscissa அச்சைக் கடக்கும் ஒருங்கிணைந்த வளைவுகளின் சாய்வின் தொடுகோடு நேர்மறை மற்றும் அதிகரிப்புடன் பூஜ்ஜியத்திலிருந்து முடிவிலிக்கு அதிகரிக்கிறது எக்ஸ்.

மணிக்கு.

பின்னர், மேலும் அதிகரிப்புடன், சாய்வின் தொடுகோடு முழுமையான மதிப்பில் குறைகிறது, எதிர்மறையாக உள்ளது மற்றும் -1 இல் முனைகிறது எக்ஸ் ® ¥ . முக்கிய ஐசோக்லைன்கள் மற்றும் ஒருங்கிணைப்பு அச்சுகளில் உள்ள ஒருங்கிணைந்த வளைவுகளுக்கு தொடுகோடுகளின் திசையை அறிந்துகொள்வது, கட்டப் பாதைகளின் முழுப் படத்தையும் உருவாக்குவது எளிது.

லியாபுனோவ் முறையைப் பயன்படுத்தி ஒருமைப் புள்ளியின் நிலைத்தன்மையின் தன்மை நிறுவப்படும். அமைப்பின் சிறப்பியல்பு நிர்ணயம் வடிவம் கொண்டது:

.

தீர்மானிப்பதை விரிவுபடுத்துவதன் மூலம், அமைப்பின் சிறப்பியல்பு சமன்பாட்டைப் பெறுகிறோம்: , அதாவது பண்புச் சமன்பாட்டின் வேர்கள் இரண்டும் எதிர்மறையானவை. எனவே, அமைப்பின் நிலையான நிலை ஒரு நிலையான முனை ஆகும். அதே நேரத்தில், பொருளின் செறிவு எக்ஸ்எப்பொழுதும் ஒரே மாதிரியாக ஒரு நிலையான நிலைக்குச் செல்கிறது, Y என்ற பொருளின் செறிவு நிமிடம் அல்லது அதிகபட்சம் கடந்து செல்லும். அத்தகைய அமைப்பில் ஊசலாட்ட ஆட்சிகள் சாத்தியமற்றது.

டெய்லர் தொடர் zol வட்டத்தில் பகுப்பாய்வு செய்யும் செயல்பாடுகளை ஆய்வு செய்வதற்கான ஒரு பயனுள்ள கருவியாக செயல்படுகிறது. வளைய மண்டலத்தில் பகுப்பாய்வு செய்யும் செயல்பாடுகளை ஆய்வு செய்ய, நேர்மறை மற்றும் எதிர்மறை சக்திகளில் (z - zq) விரிவாக்கங்களை உருவாக்க முடியும். டெய்லர் விரிவாக்கங்களைப் பொதுமைப்படுத்தும் வடிவம். இரண்டு தொடர்களின் கூட்டுத்தொகையாக விளங்கும் தொடர் (1), லாரன்ட் தொடர் என அழைக்கப்படுகிறது. தொடரின் (1) பகுதியின் ஒருங்கிணைப்பு பகுதி என்பது ஒவ்வொரு தொடரின் (2) ஒன்றிணைந்த பகுதிகளின் பொதுவான பகுதியாகும் என்பது தெளிவாகிறது. அவளைக் கண்டுபிடிப்போம். முதல் தொடரின் ஒருங்கிணைப்பு பகுதியானது, அதன் ஆரம் கௌச்சி-ஹடமார்ட் சூத்திரத்தால் தீர்மானிக்கப்படும் ஒரு வட்டமாகும். மற்றும் சீராக. இரண்டாவது தொடர் என்பது மாறியைப் பொறுத்தமட்டில் ஒரு சக்தித் தொடர் ஆகும்.தொடர் (5) அதன் வட்டத்திற்குள் ஒன்றிணைந்து m-*oo என்ற சிக்கலான மாறியின் பகுப்பாய்வுச் செயல்பாட்டிற்குச் செல்கிறது, மேலும் சிறிய ஆரம் கொண்ட எந்த வட்டத்திலும் அது முற்றிலும் மற்றும் சீராக ஒன்றிணைகிறது, அதாவது தொடரின் (4) ஒருமுகப் பகுதி என்பது வட்டத்தின் தோற்றம் - அப்படியானால் தொடரின் (3) மற்றும் (4) ஒன்றிணைக்கும் பொதுவான பகுதி இருந்தால் - ஒரு வட்ட வளையம் இதில் தொடர் (1) ஒரு பகுப்பாய்வு செயல்பாட்டிற்கு இணைகிறது. மேலும், எந்த வளையத்திலும், அது முற்றிலும் மற்றும் ஒரே மாதிரியாக ஒன்றிணைகிறது. எடுத்துக்காட்டு 1. ரேட் லாரன்ட் தொடரின் தனிமைப்படுத்தப்பட்ட ஒருமைப் புள்ளிகளின் ஒருங்கிணைப்புப் பகுதியைத் தீர்மானிக்கவும் மற்றும் அவற்றின் வகைப்பாடு (z), ஒரு வட்ட வளையத்தில் ஒற்றை மதிப்புடையது மற்றும் அரசியலற்றது, இந்த வளையத்தில் குணகங்களைக் கொண்ட ஒன்றிணைந்த தொடரின் கூட்டுத்தொகையாகக் குறிப்பிடப்படலாம். Cn தனித்துவமாக தீர்மானிக்கப்பட்டு சூத்திரங்களால் கணக்கிடப்படுகிறது, அங்கு 7p ஆரம் m வட்டம் R வளையத்திற்குள் ஒரு தன்னிச்சையான புள்ளி z ஐ சரிசெய்வோம் r புள்ளியில் மையங்களைக் கொண்ட வட்டங்களை உருவாக்குகிறோம், அதன் ஆரங்கள் ஏற்றத்தாழ்வுகளைப் பூர்த்தி செய்து புதிய வளையத்தைக் கருத்தில் கொள்கிறோம். பெருக்கல் இணைக்கப்பட்ட டொமைனுக்கான Cauchy ஒருங்கிணைந்த தேற்றத்தின்படி, எங்களிடம் உள்ளது வட்டம் 7d* உடன் உள்ள அனைத்து புள்ளிகளுக்கும் £, ஒரே சீராக குவியும் தொடர் 1 1 இன் கூட்டுத்தொகை திருப்திகரமாக உள்ளது. எனவே, பின்னம் ^ ஐ vi- /" / சற்றே வித்தியாசமான முறையில், அனைத்து புள்ளிகளுக்கும் ξ இல் குறிப்பிடலாம். வட்டம் ir> எங்களிடம் தொடர்பு உள்ளது எனவே, பின்னம் ^ என்பது சூத்திரங்களில் (10) மற்றும் (12) ஒரு வட்ட வளையத்தில் உள்ள பகுப்பாய்வு சார்புகளில் ஒரே மாதிரியான குவிந்த தொடரின் கூட்டுத்தொகையாகக் குறிப்பிடப்படலாம். எனவே, Cauchy இன் தேற்றத்தின்படி, 7/r மற்றும் 7r/ வட்டங்கள் ஏதேனும் ஒரு வட்டத்தால் மாற்றப்பட்டால், தொடர்புடைய ஒருங்கிணைப்புகளின் மதிப்புகள் மாறாது. இது சூத்திரங்களை (10) மற்றும் (12) இணைக்க அனுமதிக்கிறது.சூத்திரத்தின் (8) வலது பக்கத்தில் உள்ள ஒருங்கிணைப்புகளை முறையே அவற்றின் வெளிப்பாடுகள் (9) மற்றும் (11) மூலம் மாற்றினால், நாம் விரும்பிய விரிவாக்கத்தைப் பெறுகிறோம், ஏனெனில் z ஒரு தன்னிச்சையானது வளையத்தின் புள்ளியில், தொடர் (14) இந்த வளையத்தில் எல்லா இடங்களிலும் f(z) செயல்பாட்டிற்கு ஒன்றிணைகிறது, மேலும் எந்த வளையத்திலும் தொடர் இந்தச் செயல்பாட்டிற்கு முற்றிலும் மற்றும் ஒரே மாதிரியாக ஒன்றிணைகிறது. படிவத்தின் (6) சிதைவு தனித்துவமானது என்பதை இப்போது நிரூபிப்போம். மேலும் ஒரு சிதைவு நடைபெறுகிறது என்று வைத்துக் கொள்வோம்.பின், R வளையத்தின் உள்ளே எல்லா இடங்களிலும், சுற்றளவில், தொடர் (15) ஒரே சீராக ஒன்றிணைகிறது. சமத்துவத்தின் இரு பக்கங்களையும் பெருக்கவும் (இங்கு m என்பது ஒரு நிலையான முழு எண், மற்றும் இரண்டு தொடர் காலத்தையும் ஒருங்கிணைக்கவும். இதன் விளைவாக, நாம் இடது பக்கம், மற்றும் வலதுபுறம் - Csh. எனவே, (4, \u003d St. என்பதால். m என்பது ஒரு தன்னிச்சையான எண், அதன் குணகங்கள் சூத்திரங்கள் (7) மூலம் கணக்கிடப்படும் கடைசி சமத்துவத் தொடர் (6), லாரன்ட் தொடரின் குணகங்களுக்கு வளையம் 7 இல் உள்ள f(z) செயல்பாட்டின் லாரன்ட் தொடர் என அழைக்கப்படுகிறது. நடைமுறையில் அரிதாகவே பயன்படுத்தப்படுகிறது, ஏனெனில், ஒரு விதியாக, அவர்களுக்கு சிக்கலான கணக்கீடுகள் தேவைப்படுகின்றன. வழக்கமாக, முடிந்தால், அடிப்படை செயல்பாடுகளின் ஆயத்த டெய்லர் விரிவாக்கங்கள் பயன்படுத்தப்படுகின்றன. விரிவாக்கத்தின் தனித்துவத்தின் அடிப்படையில், எந்த முறையான முறையும் அதே முடிவுக்கு வழிவகுக்கிறது. எடுத்துக்காட்டு 2 Fuiscius /(r) க்கு இரண்டு ஒற்றைப் புள்ளிகள் இருப்பதாகக் கருதி, வெவ்வேறு டொமைன்களின் செயல்பாடுகளின் Laurent தொடர் விரிவாக்கங்களைக் கவனியுங்கள்: எனவே, மூன்று ரிங் டொமைன்கள் உள்ளன. மற்றும், புள்ளி r = 0 ஐ மையமாகக் கொண்டது. ஒவ்வொன்றிலும் f(r) செயல்பாடு பகுப்பாய்வு ஆகும்: a) வட்டமானது வட்டத்தின் வெளிப்புறமாகும் (படம் 27). இந்த ஒவ்வொரு பகுதியிலும் /(z) செயல்பாட்டின் லாரன்ட் விரிவாக்கங்களைக் கண்டுபிடிப்போம். நாம் /(z) அடிப்படை பின்னங்களின் கூட்டுத்தொகையாக பிரதிநிதித்துவப்படுத்துகிறோம் a) வட்ட உருமாற்ற உறவு (16) பின்வருமாறு ஒரு வடிவியல் முன்னேற்றத்தின் சொற்களின் கூட்டுத்தொகைக்கான சூத்திரத்தைப் பயன்படுத்தி, நாம் பெறுகிறோம் b) |z|க்கான j^j செயல்பாட்டிற்கான தொடர் (19) என்பதால், -z செயல்பாட்டிற்கான வளையம் இந்த வளையத்தில் குவிந்து கிடக்கிறது. > 1 வேறுபடுகிறது. எனவே, /(z) செயல்பாட்டைப் பின்வருமாறு மாற்றுகிறோம்: சூத்திரத்தை (19) மீண்டும் பயன்படுத்தினால், இந்தத் தொடர் ஒன்றுபடுகிறது என்பதைப் பெறுகிறோம். விரிவாக்கங்களை (18) மற்றும் (21) தொடர்புக்கு (20) மாற்றினால், c) வட்டத்தின் வெளிப்புறத்தை -z உடன் |z| > 2 வேறுபட்டது, மற்றும் செயல்பாட்டிற்கான தொடர் (21) பின்வரும் வடிவத்தில் /(z) செயல்பாட்டைப் பிரதிநிதித்துவப்படுத்துவோம்: /<*> (18) மற்றும் (19) சூத்திரங்களைப் பயன்படுத்தி, OR 1 ஐப் பெறுகிறோம், அதே செயல்பாட்டிற்கு f(z) லாரன்ட் விரிவாக்கம், பொதுவாகச் சொன்னால், வெவ்வேறு வளையங்களுக்கு வெவ்வேறு வடிவத்தைக் கொண்டுள்ளது என்பதை இந்த எடுத்துக்காட்டு காட்டுகிறது. எடுத்துக்காட்டு 3. லாரன்ட் தொடரின் 8 லாரன்ட் தொடரின் சிதைவைக் கண்டறியவும், லாரன்ட் தொடரின் தனிமைப்படுத்தப்பட்ட ஒருமைப் புள்ளிகள் மற்றும் வருடாந்திர மண்டலத்தில் அவற்றின் வகைப்பாடு A பின்வரும் வடிவத்தில் f (z) செயல்பாட்டின் பிரதிநிதித்துவத்தைப் பயன்படுத்துகிறோம்: மற்றும் இரண்டாவது வார்த்தையைப் பயன்படுத்தி மாற்றவும் ஒரு வடிவியல் முன்னேற்றத்தின் விதிமுறைகளின் கூட்டுத்தொகைக்கான சூத்திரம், நாம் கண்டுபிடிக்கப்பட்ட வெளிப்பாடுகளை சூத்திரத்தில் (22) மாற்றியமைக்கிறோம், எங்களிடம் எடுத்துக்காட்டு 4 உள்ளது. மெல்லிய zq = 0 இன் அருகில் உள்ள லாரன்ட் தொடரில் செயல்பாட்டை விரிவுபடுத்தவும். எந்தவொரு சிக்கலான ஒன்றிற்கும் , எங்களிடம் இந்த விரிவாக்கம் எந்தப் புள்ளிக்கும் செல்லுபடியாகும் z Ф 0. இந்த விஷயத்தில், வளையப் பகுதி என்பது z - 0 என்ற ஒரு புள்ளியைக் கொண்ட முழு சிக்கலான விமானமாகும். இந்தப் பகுதியை பின்வரும் உறவின் மூலம் வரையறுக்கலாம்: இந்த செயல்பாடு பகுப்பாய்வு ஆகும் பிராந்தியத்தில் லாரன்ட் தொடரின் குணகங்களுக்கான சூத்திரங்கள் (13) இலிருந்து, முந்தைய பத்தியில் உள்ள அதே பகுத்தறிவின் மூலம், ஒருவர் Kouiw ஏற்றத்தாழ்வுகளைப் பெறலாம். F(z) சார்பு ஒரு வட்டத்தில் வரம்பிடப்பட்டால், அங்கு M ஒரு மாறிலி), பின்னர் தனிமைப்படுத்தப்பட்ட ஒருமைப் புள்ளிகள் A புள்ளி zo ஆனது, புள்ளியின் வருடாந்திர சுற்றுப்புறம் இருந்தால், f(z) செயல்பாட்டின் தனிமைப்படுத்தப்பட்ட ஒருமைப் புள்ளி என்று அழைக்கப்படுகிறது ( இந்த தொகுப்பு சில நேரங்களில் புள்ளி 2o இன் துளையிடப்பட்ட சுற்றுப்புறம் என்றும் அழைக்கப்படுகிறது, இதில் f(z) செயல்பாடு ஒற்றை மதிப்பு மற்றும் பகுப்பாய்வு ஆகும். புள்ளி zo இல், செயல்பாடு வரையறுக்கப்படவில்லை அல்லது ஒற்றை மதிப்பு மற்றும் பகுப்பாய்வு இல்லை. zo புள்ளியை அணுகும்போது /(z) செயல்பாட்டின் நடத்தையைப் பொறுத்து மூன்று வகையான ஒற்றைப் புள்ளிகள் வேறுபடுகின்றன. ஒரு தனிமைப்படுத்தப்பட்ட ஒருமைப் புள்ளி கூறப்படும்: 1) வரையறுக்கப்பட்ட இருந்தால் நீக்கக்கூடியது 2) pmusach என்றால் 3) f(z) சார்புக்கு வரம்பு இல்லை எனில் அடிப்படையில் ஒருமைப் புள்ளி தேற்றம் 16. f(z) செயல்பாட்டின் தனிமைப்படுத்தப்பட்ட ஒருமைப் புள்ளி z0 என்பது, zo புள்ளியின் அருகில் உள்ள f(z) செயல்பாட்டின் லாரன்ட் விரிவாக்கம் ஒரு முக்கியப் பகுதியைக் கொண்டிருக்கவில்லை என்றால் மட்டுமே நீக்கக்கூடிய ஒருமைப் புள்ளியாகும், அதாவது. லெட் சோ வடிவத்தைக் கொண்டுள்ளது - நீக்கக்கூடிய ஒற்றைப் புள்ளி. பின்னர் ஒரு வரையறுக்கப்பட்ட செயல்பாடு உள்ளது, எனவே, f(z) சார்பு r என்ற புள்ளியின் ப்ரோகோலாஜிக்கல் சுற்றுப்புறத்தில் வரம்பிடப்பட்டுள்ளது. Cauchy ஏற்றத்தாழ்வுகளின் அடிப்படையில் நாம் அமைக்கிறோம், ஏனெனில் p ஐ தன்னிச்சையாக சிறியதாக தேர்வு செய்யலாம், பின்னர் அனைத்து குணகங்களும் எதிர்மறை சக்திகள் (z - 20) பூஜ்ஜியத்திற்கு சமம்: மாறாக, லாரன்ட் zq புள்ளியின் சுற்றுப்புறத்தில் /(r) செயல்பாட்டின் விரிவாக்கம் சரியான பகுதியை மட்டுமே கொண்டுள்ளது, அதாவது, அது வடிவம் (23) மற்றும், இதன் விளைவாக, டெய்லர். z -* z0 க்கு செயல்பாடு /(r) வரம்பு மதிப்பைக் கொண்டிருப்பதைக் காண்பது எளிது: தேற்றம் 17. F(z) செயல்பாட்டின் தனிமைப்படுத்தப்பட்ட ஒருமைப் புள்ளி zq ஆனது J(z) செயல்பாடாக இருந்தால் மட்டுமே நீக்கப்படும். புள்ளி zq, Zgmechai இல்லை. r0 என்பது f(r) இன் நீக்கக்கூடிய ஒற்றைப் புள்ளியாக இருக்கட்டும். வது புள்ளியை மையமாகக் கொண்ட சில வட்டத்தில் f(r) செயல்பாடு பகுப்பாய்வு என்று நாம் கருதுகிறோம். இது புள்ளியின் பெயரை வரையறுக்கிறது - செலவழிப்பு. தேற்றம் 18. f(z) செயல்பாட்டின் தனிமைப்படுத்தப்பட்ட ஒருமைப் புள்ளி zq என்பது ஒரு துருவமாகும், அது புள்ளியின் அருகில் உள்ள f(z) செயல்பாட்டின் லாரன்ட் விரிவாக்கத்தின் முக்கிய பகுதி வரையறுக்கப்பட்ட (மற்றும் நேர்மறை) எண்ணைக் கொண்டிருந்தால் மட்டுமே. பூஜ்ஜியமற்ற சொற்கள், அதாவது, வடிவம் 4 உள்ளது z0 ஒரு துருவமாக இருக்கட்டும். அப்போதிருந்து, புள்ளி z0 இன் துளையிடப்பட்ட சுற்றுப்புறம் உள்ளது, இதில் f(z) செயல்பாடு பகுப்பாய்வு மற்றும் பூஜ்ஜியமற்றது. பின்னர் இந்த சுற்றுப்புறத்தில் ஒரு பகுப்பாய்வு செயல்பாடு வரையறுக்கப்படுகிறது, எனவே, புள்ளி zq என்பது செயல்பாட்டின் நீக்கக்கூடிய ஒருமை புள்ளி (பூஜ்ஜியம்) அல்லது h(z) ஒரு பகுப்பாய்வு சார்பு, h(z0) ∩ 0. புள்ளி zq, எனவே, நாம் அதை எங்கிருந்து பெறுகிறோம், இப்போது f(z) சார்பு zo புள்ளியின் துளையிடப்பட்ட பகுதியில் உள்ள வடிவத்தின் (24) சிதைவைக் கொண்டுள்ளது என்று வைத்துக்கொள்வோம். இதன் பொருள், இந்தச் சூழலில் f(z) சார்பு, செயல்பாட்டுடன் சேர்ந்து பகுப்பாய்வு செய்யப்படுகிறது. g(z) செயல்பாட்டிற்கு, விரிவாக்கம் செல்லுபடியாகும், அதில் இருந்து zq என்பது g(z) செயல்பாட்டின் நீக்கக்கூடிய ஒருமைப் புள்ளி என்பது தெளிவாகிறது, மேலும் செயல்பாடு 0-ல் இருக்கும் - செயல்பாட்டின் துருவத்தில் இன்னும் எளிமையான ஒன்று உள்ளது. உண்மை. புள்ளி Zq என்பது f(z) செயல்பாட்டின் ஒரு துருவமாகும், g(z) = y சார்பு g(z0) = 0 ஐ அமைப்பதன் மூலம் zq புள்ளியின் சுற்றுப்புறத்தில் ஒரு பகுப்பாய்வு செயல்பாட்டிற்கு நீட்டிக்கப்பட்டால் மட்டுமே. f(z) செயல்பாட்டின் துருவமானது jfa செயல்பாட்டின் பூஜ்ஜியத்தின் வரிசை எனப்படும். 16 மற்றும் 18 கோட்பாடுகள் பின்வரும் வலியுறுத்தலைக் குறிக்கின்றன. தேற்றம் 19. இந்த புள்ளியின் துளையிடப்பட்ட சுற்றுப்புறத்தில் உள்ள லாரன்ட் விரிவாக்கத்தின் முக்கிய பகுதி எண்ணற்ற பல பூஜ்ஜியமற்ற சொற்களைக் கொண்டிருந்தால் மட்டுமே தனிமைப்படுத்தப்பட்ட ஒருமை மெல்லியதாக இருக்கும். எடுத்துக்காட்டு 5. செயல்பாட்டின் ஒருமைப் புள்ளி zo = 0. எங்களிடம் Laurent Series தனிமைப்படுத்தப்பட்ட ஒருமைப் புள்ளிகள் உள்ளன மற்றும் அவற்றின் வகைப்பாடு எனவே, zo = 0 என்பது நீக்கக்கூடிய ஒருமைப் புள்ளியாகும். பூஜ்ஜியப் புள்ளிக்கு அருகில் உள்ள Laurent தொடரில் /(z) செயல்பாட்டின் விரிவாக்கம் சரியான பகுதியை மட்டுமே கொண்டுள்ளது: Example7. f(z) = செயல்பாட்டின் ஒருமைப் புள்ளி f(z) zq = 0. உண்மையான மற்றும் கற்பனை அச்சுகளில் இந்தச் செயல்பாட்டின் நடத்தையைக் கவனியுங்கள்: உண்மையான அச்சில் x 0, கற்பனை அச்சில் எனவே, வரையறுக்கப்பட்டதாகவோ இல்லை z -* 0 இல் எல்லையற்ற வரம்பு f(z) இல்லை. எனவே புள்ளி r0 = 0 என்பது f(z) செயல்பாட்டின் அடிப்படையில் ஒருமைப் புள்ளியாகும். பூஜ்ஜியப் புள்ளியின் சுற்றுப்புறத்தில் f(z) செயல்பாட்டின் லாரன்ட் விரிவாக்கத்தைக் கண்டுபிடிப்போம். எந்தவொரு சிக்கலான சிக்கும் நாங்கள் அமைத்துள்ளோம். பின்னர் Laurent விரிவாக்கம் z இன் எதிர்மறை சக்திகளுடன் எண்ணற்ற சொற்களைக் கொண்டுள்ளது.

விடுங்கள் zq - செயல்பாட்டின் ஒருமை புள்ளி f(z), t.s. f(z)ஆனால் இந்த கட்டத்தில் பகுப்பாய்வு செய்யப்படுகிறது (குறிப்பாக, அதில் வரையறுக்கப்படாமல் இருக்கலாம்). புள்ளியின் அத்தகைய துளையிடப்பட்ட சுற்றுப்புறம் இருந்தால் zq (அதாவது, O z தொகுப்பு - zq f(z) என்பது மாற்றுப்பெயர், பின்னர் zoஅழைக்கப்பட்டது தனிமைப்படுத்தப்பட்ட ஒற்றை புள்ளிசெயல்பாடுகள் f(z)இந்த வரையறை வழக்கில் பாதுகாக்கப்படுகிறது zn =ஓ, அயோடின் ஒரு புள்ளியின் துளையிடப்பட்ட சுற்றுப்புறமாக இருந்தால் zq = oo தொகுப்பைப் புரிந்து கொள்ளுங்கள் z >நான் - தோற்றத்தை மையமாகக் கொண்ட சில வட்டத்தின் தோற்றம். வேறு வார்த்தைகளில் கூறுவதானால், ஒருமை புள்ளி zq தனிமைப்படுத்தப்பட்டதாகக் கூறப்படுகிறது, இந்தப் புள்ளியின் சுற்றுப்புறம் இருந்தால், அதில் வேறு ஒருமைப் புள்ளிகள் உள்ளன. zq கீழே உள்ள எல்லா இடங்களிலும், ஒரு மதிப்புள்ள எழுத்தின் (செயல்பாடு) ஒருமைப் புள்ளிகளை மட்டுமே நாங்கள் கருதுகிறோம் f(z)தனித்துவமானது என்று கருதப்படுகிறது).

செயல்பாட்டின் நடத்தையைப் பொறுத்து f(z)மணிக்கு z -> zqஒருமைப் புள்ளிகளில் மூன்று வகைகள் உள்ளன. தனிமைப்படுத்தப்பட்ட ஒற்றை புள்ளி zq செயல்பாடுகள் f(z)அழைக்கப்பட்டது:

1) நீக்கக்கூடிய ஒற்றை புள்ளிவரையறுக்கப்பட்ட வரம்பு இருந்தால்

2) கம்பம்ஒரு வரம்பு இருந்தால்

3) அத்தியாவசிய புள்ளி,என்றால் f(z) க்கு வரையறுக்கப்பட்ட அல்லது எல்லையற்ற வரம்பு இல்லை z-> zq.

எடுத்துக்காட்டு 26.1. மூன்று வகையான ஒருமைப் புள்ளிகளும் உணரப்பட்டதாகக் காட்டுவோம். கருத்தில் கொள்ளுங்கள் f(z)= புள்ளி zq = 0 தனிமைப்படுத்தப்பட்டது

இந்த செயல்பாட்டின் ஒருமை புள்ளி. சூத்திரத்தைப் பயன்படுத்தி (22.12), விரிவாக்கத்தைப் பெறுகிறோம்

அதிலிருந்து லிம் உள்ளது என்று தெரிகிறது fi(z)= 1. எனவே, zq = 0 ஆகும்

செயல்பாட்டின் நீக்கக்கூடிய ஒற்றைப் புள்ளி fi(z)

செயல்பாடு f'j(z) =--- ஒரு புள்ளியில் ஒரு கம்பம் உள்ளது zo= 1 ஏனெனில்

2 ஆர்" எக்ஸ்

இப்போது செயல்பாட்டைக் கவனியுங்கள் )z(z)= e 1 ^ r மற்றும் அதைக் காட்டு zo = O என்பது இந்தச் செயல்பாட்டின் இன்றியமையாத ஒருமைப் புள்ளியாகும். முயற்சி செய்யும் போது zஉண்மையான அச்சில் பூஜ்ஜியத்திற்கு, f செயல்பாட்டின் இடது மற்றும் வலது வரம்புகள் (z)வேறுபட்டது: லிம் உடன் 1 / 1 = 0,லிம் 1 /* = உடன் os. இது குறிக்கிறது,

x->0-0 x->0+O

என்ன f:i(z) 2க்கு வரையறுக்கப்பட்ட அல்லது எல்லையற்ற வரம்பு இல்லை -> ஓ, அதாவது zq = 0 என்பது இந்தச் செயல்பாட்டின் அடிப்படையில் ஒருமைப் புள்ளியாகும். (புள்ளியின் போக்கில் என்பதை நினைவில் கொள்க z-iyகற்பனை அச்சு செயல்பாட்டில் பூஜ்ஜியத்திற்கு

வரம்பு இல்லை.)

நிச்சயமாக, தனிமைப்படுத்தப்படாத ஒற்றை புள்ளிகளும் உள்ளன. உதாரணத்திற்கு. செயல்பாடு புள்ளிகளில் துருவங்களைக் கொண்டுள்ளது z n = -, பி= ±1, ±2,...

இதன் விளைவாக, Zq = 0 என்பது இந்தச் செயல்பாட்டின் தனிமைப்படுத்தப்படாத ஒருமைப் புள்ளியாகும்: இந்தப் புள்ளியின் எந்த (தன்னிச்சையாக சிறிய) சுற்றுப்புறத்திலும் பிற ஒருமைப் புள்ளிகள் உள்ளன. g p.

விடுங்கள் zo-ஒரு செயல்பாட்டின் இறுதி தனிமைப்படுத்தப்பட்ட ஒற்றை புள்ளி f(z)பிறகு f(z)புள்ளியின் சில துளையிடப்பட்ட சுற்றுப்புறங்களில் 0 Zo போன்றது zoஇந்த சுற்றுப்புறத்தை உள் ஆரம் r = 0 கொண்ட வளையமாகக் கருதலாம். தேற்றம் 25.1 மூலம், பரிசீலனையில் உள்ள சுற்றுப்புறத்தில், செயல்பாடு f(z)லாரன்ட் தொடரில் (25.2) விரிவாக்க முடியும். 2க்கான செயல்பாட்டின் நடத்தையைக் காட்டுவோம் -> zq (அதாவது ஒருமைப் புள்ளியின் வகை zo)சிதைவின் முக்கிய பகுதியின் வடிவத்தை சார்ந்துள்ளது (25.2); இந்த சூழ்நிலை "முக்கிய பகுதி" என்ற வார்த்தையின் தோற்றத்தை விளக்குகிறது.

கோட்பாடு 2G.2. f(z) செயல்பாட்டின் தனிமைப்படுத்தப்பட்ட ஒருமைப் புள்ளி zo இந்த புள்ளியின் துளையிடப்பட்ட சுற்றுப்புறத்தில் உள்ள Lorap விரிவாக்கம் oid இருந்தால் மட்டுமே நீக்கப்படும்.

அந்த. சரியான பகுதியை மட்டுமே கொண்டுள்ளது, மற்றும் முக்கிய பகுதியின் அனைத்து குணகங்களும் புல்லட்டிற்கு சமம்.

ஆதாரம். 1. விடுங்கள் zoஒரு நீக்கக்கூடிய ஒற்றை புள்ளியாகும். லாரன்ட் செயல்பாட்டின் விரிவாக்கம் என்பதை நிரூபிப்போம் f(z)வடிவம் (26.1) உள்ளது. ஒற்றைப் புள்ளி என்பதால் zoநீக்கக்கூடியது, பின்னர் ஒரு வரையறுக்கப்பட்ட வரம்பு லிம் உள்ளது f(z) = A.இதன் விளைவாக, f(z)சில துளையிடப்பட்ட சுற்றுப்புறங்களில் 0 z - புள்ளியின் zq வரை கட்டுப்படுத்தப்பட்டுள்ளது zo,அந்த. )(z) அனைவருக்கும் zஇந்த சுற்றுப்புறத்தில் இருந்து. ஏதேனும் எடுத்துக் கொள்ளுங்கள் ஆர். U р /?|, மற்றும் லாரன்ட் தொடரின் குணகங்களுக்கு சூத்திரங்களை (25.3) பயன்படுத்தவும்:

விரிவாக்கத்தின் முக்கிய பகுதியின் குணகங்களுக்கு n =- 1,-2,... அத்தகைய மதிப்புகளுக்கு பிஎங்களிடம் உள்ளது p~n-இ 0 மணிக்கு ஆர்-> 0. மதிப்பு இருந்து ஆர்தன்னிச்சையாக சிறியதாக தேர்வு செய்யலாம் திரு~"தன்னிச்சையாக சிறியதாக இருக்கலாம். இருந்து |c t,| ^ திருமற்றும் cn p ஐ சார்ந்து இல்லை, பிறகு cn = 0 க்கு மற்றும்= - 1, -2,..., இது நிரூபிக்கப்பட இருந்தது.

2. இப்போது Laurent விரிவாக்கம் வடிவம் (26.1) உள்ளது என்று வைத்துக்கொள்வோம். தொடர் (26.1) ஒரு சக்தி தொடர் மற்றும். எனவே, துளையிடப்பட்ட இடத்தில் மட்டுமல்ல, முழு சுற்றுப்புறத்திலும் கூடுகிறது z-zq புள்ளி உட்பட zo;அதன் அளவு S(z)என்பதற்கான பகுப்பாய்வு ஆகும் z மற்றும் S(z) = )(z) 0 z இல் - zoஆர்.எனவே, ஒரு வரையறுக்கப்பட்ட வரம்பு உள்ளது )(z)\u003d Pm 5 (r) \u003d 5 (r) - எனவே, ஒருமைப் புள்ளி zq

Z->Zo Z-*Zo

செலவழிக்கக்கூடியது. தேற்றம் நிரூபிக்கப்பட்டுள்ளது.

கருத்து. இது தேற்றத்தின் நிரூபணத்திலிருந்து பின்வருமாறு, ஒரு துளையிடப்பட்ட சுற்றுப்புறத்தில் 0 z - zo நீக்கக்கூடிய ஒருமை புள்ளியின், செயல்பாடு f(z)செயல்பாடு S(r) உடன் ஒத்துப்போகிறது, இது முழு சுற்றுப்புறத்திலும் பகுப்பாய்வு செய்யப்படுகிறது z - zo எனவே, /(th) = என்று வைத்தால் S(zq), பின்னர், செயல்பாட்டின் மதிப்புகளை மாற்றாமல் f(z)துளையிடப்பட்ட சுற்றுப்புறத்தின் எந்தப் புள்ளியிலும், இந்தச் செயல்பாட்டை r இல் பகுப்பாய்வு செய்கிறோம், அதாவது. அம்சத்தை "நீக்கு". இது "நீக்கக்கூடிய ஒருமை" என்ற சொல்லை விளக்குகிறது. அத்தகைய புள்ளிகளை வழக்கமானதாகக் கருதுவது இயற்கையானது, செயல்பாட்டின் ஒருமைப் புள்ளிகள் அல்ல f(z)

எடுத்துக்காட்டாக, செயல்பாட்டைக் கவனியுங்கள்

எடுத்துக்காட்டு 26.1 இல், Pm (n) = 1. அதாவது. ஒருமை புள்ளி

zq = 0 நீக்கக்கூடியது. அமைத்தல் /i(0) = 1, இதன் மூலம் ஒருமைப்பாட்டை நீக்கி, புள்ளியில் பகுப்பாய்வு செய்யும் செயல்பாட்டைப் பெறுகிறோம் zq = 0 (மற்றும் முழு விமானம் C இல்).

லாரன்ட் விரிவாக்கங்களின் அடிப்படையில் துருவங்களை இப்போது வகைப்படுத்துவோம்.

தேற்றம் 26.3. f(z) செயல்பாட்டின் தனிமைப்படுத்தப்பட்ட ஒருமைப் புள்ளி Zo என்பது ஒரு துருவம் என்றால் மற்றும் இருந்தால் மட்டுமே, Zq மையத்துடன் கூடிய Laurent விரிவாக்கத்தின் முக்கிய பகுதியானது வரையறுக்கப்பட்ட எண்ணிக்கையை மட்டுமே கொண்டிருக்கும் போது

n உடன் பூஜ்ஜிய குணகங்களிலிருந்து:

ஆதாரம். 1. விடுங்கள் zq - துருவம், அதாவது. லிம் /( z) = ஓ.

லாரன்ட் செயல்பாட்டின் விரிவாக்கம் என்பதை நிரூபிப்போம் f(z)வடிவம் (2G.2) உள்ளது. லிம்மிலிருந்து f(z)= ஓ. பின்னர் புள்ளியின் ஒரு துளையிடப்பட்ட சுற்றுப்புறம் உள்ளது

கி zq இதில் f(z)பகுப்பாய்வு மற்றும் பூஜ்ஜியங்கள் இல்லை. பின்னர் செயல்பாடு g(z) = 1 /f(z)இந்த துளையிடப்பட்ட சுற்றுப்புறத்திலும் பகுப்பாய்வு இருக்கும், மற்றும் லிம் g(z)= 0. எனவே, ஜோசெலவழிக்கக்கூடியது *-? *0

செயல்பாட்டின் ஒருமை புள்ளி g(z)மறுவரையறை செய்வோம் g(z)புள்ளியில் zo, போடுதல் g(zo)= 0. பிறகு g(z)(துளையிடப்படாத) புள்ளியின் முழு சுற்றுப்புறத்திலும் பகுப்பாய்வு செய்யப்படுகிறது z 0,மற்றும் z0அதன் தனிமைப்படுத்தப்பட்ட பூஜ்ஜியமாக இருக்கும். மூலம் குறிக்கவும் என்இந்த பூஜ்ஜியத்தின் பெருக்கம் (வரிசை). §23 இல் காட்டப்பட்டுள்ளபடி, புள்ளியின் சுற்றுப்புறத்தில் zq செயல்பாடு g(z)வடிவத்தில் குறிப்பிடக்கூடியது (பார்க்க (23.2))

மற்றும் (z$) f 0 மற்றும் y>(z)புள்ளியின் சில சுற்றுப்புறங்களில் பகுப்பாய்வு ஆகும் zo-ஏனெனில் ip(z)புள்ளியில் தொடர்ந்து zoமற்றும் g>(zo) எஃப் 0" பிறகு ip(z)இந்த புள்ளியின் சில சுற்றுப்புறங்களில் பூஜ்ஜியங்கள் இல்லை. எனவே செயல்பாடு 1 /-p(z)இந்த சுற்றுப்புறத்திலும் பகுப்பாய்வு இருக்கும், எனவே, டெய்லர் தொடரில் விரிவடைகிறது:

அடைப்புக்குறிகளைத் திறந்து, குணகங்களின் பெயர்களை மாற்றுவதன் மூலம், கடைசி விரிவாக்கத்தை வடிவத்தில் எழுதுகிறோம்

எங்கே c_jv = 1>o f 0. எனவே, f(r) இன் Laurent விரிவாக்கத்தின் முக்கிய பகுதியானது வரையறுக்கப்பட்ட எண்ணிக்கையிலான சொற்களை மட்டுமே கொண்டுள்ளது; தேவையான சமத்துவத்தை நாங்கள் அடைந்துள்ளோம் (26.2).

2. ஒரு புள்ளியின் துளையிடப்பட்ட சுற்றுப்புறத்தில் இருக்கட்டும் வதுசெயல்பாடு )(z)லாரன்ட் விரிவாக்கத்தால் (26.2) குறிப்பிடப்படுகிறது (மேலும் விரிவாக்கப்பட்ட வடிவத்தில், பார்க்க (26.3)), இதன் முக்கிய பகுதியானது வரையறுக்கப்பட்ட எண்ணிக்கையிலான சொற்களை மட்டுமே கொண்டுள்ளது, மேலும் உடன்- d" f 0. நாம் அதை நிரூபிக்க வேண்டும் Zq - செயல்பாட்டு துருவம் f(z)சமத்துவத்தை (26.3) ஆல் பெருக்குதல் (ஜி - ஜி o) iV , நாங்கள் செயல்பாட்டைப் பெறுகிறோம்

(26.4) இல் உள்ள தொடர் ஒரு பவர் சீரிஸ் ஆகும், இது பஞ்சர் செய்யப்பட்ட இடத்தில் மட்டுமல்ல, புள்ளியின் முழு சுற்றுப்புறத்திலும் ஒரு பகுப்பாய்வு செயல்பாட்டிற்கு மாறுகிறது. Zq. எனவே, செயல்பாடு h(z)நாம் அமைப்பதன் மூலம் அதை நீட்டித்தால், இந்த சுற்றுப்புறத்தில் பகுப்பாய்வு ஆகிறது h(zo)= s_dg f 0. பிறகு

எனவே புள்ளி o ஒரு துருவமாகும், மேலும் தேற்றம் 26.3 நிரூபிக்கப்பட்டுள்ளது.

பூஜ்ஜிய செயல்பாட்டின் பன்முகத்தன்மை (வரிசை). g(z)= 1//(r) அழைக்கப்படுகிறது துருவ ஒழுங்குசெயல்பாடு /(r). ஒரு என்றால் N-துருவத்தின் வரிசை வது, பின்னர் g(z)= (ஆர் - Zo)N ip(z),செல்) எஃப் 0, மற்றும், தேற்றம் 26.3 இன் ஆதாரத்தின் முதல் பகுதியில் காட்டப்பட்டுள்ளபடி, f(r) இன் விரிவாக்கம் வடிவம் (26.3), அங்கு c_/v f 0. மாறாக, f(r) தொடராக விரிவடைந்தால் (26.3) மற்றும் e-z F 0, பின்னர்

டி.எஸ். N- f(r) செயல்பாட்டின் துருவத்தின் வரிசை. இந்த வழியில், செயல்பாட்டின் zq துருவத்தின் வரிசை/(ஜி) புள்ளி zq இன் துளையிடப்பட்ட சுற்றுப்புறத்தில் உள்ள லாரன்ட் விரிவாக்கத்தின் முக்கிய பகுதியின் முன்னணி பூஜ்ஜியமற்ற குணகத்தின் எண்ணிக்கைக்கு சமம்(அதாவது அத்தகைய எண்ணுக்கு சமம் N,என்ன s_dg f 0 மற்றும் sp= 0 மணிக்கு பி > N).

பின்வரும் உறுதிமொழியை நிரூபிப்போம், இது வசதியானது) பயன்பாடுகளுக்கு.

முடிவு 26.4. புள்ளி zq என்பது புனைகதையின் வரிசை N இன் துருவமாகும்/(ஜி) என்றால் மற்றும் இருந்தால் மட்டுமே/(ஜி) வடிவத்தில் குறிப்பிடுகின்றன

இங்கு h(z) என்பது ஒரு புள்ளியின் சுற்றுப்புறத்தில் உள்ள ஒரு பகுப்பாய்வு செயல்பாடு ஆகும்வது மற்றும் h(zo) f 0.

ஆதாரம். செயல்பாடு cp(z) = l/h(z)புள்ளி r இன் சில சுற்றுப்புறங்களில் பகுப்பாய்வு ஆகும். 26.4 இன் நிபந்தனை பின்வருவனவற்றிற்கு சமம்:

அதனால் தான் zq - பெருக்கல் பூஜ்யம் என்செயல்பாடுகள் g(z)மற்றும் அதனால் பன்மடங்கு துருவம் என்செயல்பாடுகள் /(2).

II உதாரணம் 26.5. ஒரு செயல்பாட்டின் தனிமைப்படுத்தப்பட்ட ஒற்றை புள்ளிகளைக் கண்டறியவும் மற்றும் அவற்றின் வகையை தீர்மானிக்கவும்.

D e u c tio n. இதில் உள்ள புள்ளிகள் (z 2 + 1 )(z+ எச்) 2 = 0. என்றால் z 2 எல்- 1 = 0 பின்னர் 2 = ± கிராம்என்றால் (z 4- எச்) 2 = 0, பின்னர் z= -3. எனவே, செயல்பாடு மூன்று ஒற்றை புள்ளிகளைக் கொண்டுள்ளது z= ஆர், 22 = -ஆர், Z3 = - 3. கருத்தில் z:

ஜி -முதல்-வரிசை துருவம் (நாங்கள் முடிவு 26.4 ஐப் பயன்படுத்தினோம்). 22 = என்று இதேபோல் நிரூபிக்கலாம் -நான்முதல் வரிசையின் துருவமும் கூட. 2 மணிநேரத்திற்கு எங்களிடம் உள்ளது:

அடிப்படையில் ஒருமைப் புள்ளிகளைக் கருத்தில் கொள்வோம்.

தேற்றம் 26.6. zqஐ மையமாகக் கொண்ட லாரன்ட் விரிவாக்கத்தின் முக்கியப் பகுதியானது எண்ணற்ற வேறுபாட்டைக் கொண்டிருந்தால் மட்டுமே f(z) செயல்பாட்டின் தனிமைப்படுத்தப்பட்ட ஒருமைப் புள்ளி zq அடிப்படையில் ஒருமையாக இருக்கும். பூஜ்யம், p உடன் குணகங்கள்.

ஆதாரம். தேற்றம் 26.6 நேரடியாக கோட்பாடுகள் 26.2 மற்றும் 26.3 இலிருந்து பின்பற்றுகிறது. உண்மையில், புள்ளி என்றால் zq என்பது அடிப்படையில் ஒருமை, பின்னர் லாரன்ட் விரிவாக்கத்தின் முக்கிய பகுதி இல்லாமல் இருக்க முடியாது அல்லது வரையறுக்கப்பட்ட எண்ணிக்கையிலான சொற்களைக் கொண்டிருக்க முடியாது (இல்லையெனில் புள்ளி Zq என்பது நீக்கக்கூடியதாகவோ அல்லது துருவமாகவோ இருக்கும்). எனவே, முக்கிய பகுதியில் உள்ள சொற்களின் எண்ணிக்கை எல்லையற்றதாக இருக்க வேண்டும்.

மாறாக, முக்கிய பகுதியில் எண்ணற்ற உறுப்பினர்கள் இருந்தால், பிறகு Zq என்பது நீக்கக்கூடிய புள்ளியாகவோ அல்லது துருவமாகவோ இருக்க முடியாது. இதன் விளைவாக, இந்த புள்ளி அடிப்படையில் ஒருமையாக உள்ளது.

வரையறையின்படி, f(2) சார்புக்கு வரையறுக்கப்பட்ட அல்லது எல்லையற்ற வரம்பு இல்லை என்பதன் அடிப்படையில் ஒருமைப் புள்ளி வகைப்படுத்தப்படுகிறது. z ->zq அடிப்படையில் ஒருமைப் புள்ளியின் சுற்றுப்புறத்தில் ஒரு செயல்பாட்டின் நடத்தை எவ்வளவு ஒழுங்கற்றது என்பது பற்றிய முழுமையான யோசனை பின்வரும் தேற்றத்தால் வழங்கப்படுகிறது.

தேற்றம் 26.7 (சோச்சோக்கியின் தேற்றம்). zq என்பது ஒருமையில் இருந்தால், செயல்பாட்டின் புள்ளி f(z), பின்னர் எந்த கலப்பு எண்ணுக்கும்எல், A = உட்படஓ, z n புள்ளிகளின் வரிசை உள்ளது, அதாவது z n -> zo மற்றும்லிம் f(zn) = ஆனால்.

n->os

ஆதாரம். முதலில் வழக்கைக் கவனியுங்கள் ஏ =ஓ. தேற்றம் 2G.2 இன் நிரூபணத்தின் முதல் பகுதியில், என்றால் என்று நிறுவினோம் f(z)புள்ளி r0 இன் சில துளையிடப்பட்ட சுற்றுப்புறத்தில் கட்டுப்படுத்தப்படுகிறது, பின்னர் அனைத்து குணகங்களும் c, n = - 1, - 2,... முக்கியப் பகுதி பூஜ்ஜியத்திற்குச் சமம் (இதன் விளைவாக, th இல் உள்ள ஒருமை நீக்கக்கூடியது). அனுமானத்தின் மூலம் r0 என்பது அடிப்படையில் ஒருமைப் புள்ளியாக இருப்பதால், r0 புள்ளியின் எந்த துளையிடப்பட்ட சுற்றுப்புறத்திலும் f(r) சார்பு வரம்பற்றது. சில குறுகிய சுற்றுப்புறத்தை 0 Z எடுத்துக்கொள்வோம் f(zi) > 1 (என்றால் |/(r)| z - zo R/2 இல் ஒரு புள்ளி உள்ளது z-2 , எங்கே |/(dd)| > 2, முதலியன: துளையிடப்பட்ட சுற்றுப்புறத்தில் O 71. rn -e go மற்றும் lim /(r«) = oo என்பது வெளிப்படையானது. எனவே, வழக்கில் A = oo, தேற்றம் 26.7

நிரூபிக்கப்பட்டுள்ளது.

இப்போது விடுங்கள் ஒரு எஃப்ஓ. முதலில் ஒரு துளையிடப்பட்ட அக்கம் 0 உள்ளது என்று வைத்துக் கொள்வோம்

= -yy---- இந்த துளையிடப்பட்ட சுற்றுப்புறத்தில் பகுப்பாய்வு இருக்கும், அதன் விளைவாக,

/(ஜி) ​​- ஆனால்

இதன் விளைவாக, r என்பது Φ(r) செயல்பாட்டின் தனிமைப்படுத்தப்பட்ட ஒருமைப் புள்ளியாகும். காட்டுவோம். r0 என்பது Φ(r) இன் அடிப்படையில் ஒருமைப் புள்ளியாகும். அது தவறாக இருக்கட்டும். பின்னர் ஒரு வரம்பு லிம் Φ(r), வரையறுக்கப்பட்ட அல்லது எல்லையற்றது. ஏனெனில்

/(r) = A +, பின்னர் Hsh /(r) உள்ளது, இது நிபந்தனைக்கு முரணானது

F(g) ~ :-*z 0

தேற்றத்தின் பார்வை. எனவே r0 என்பது Φ(r) செயல்பாட்டின் அடிப்படையில் ஒருமைப் புள்ளியாகும். மேலே நிரூபிக்கப்பட்டவற்றின் படி, r n புள்ளிகளின் வரிசை உள்ளது, அதாவது r n o மற்றும் lim Φ(r n) = oo. இங்கிருந்து

f(r) என்ற அனுமானத்தின் கீழ் தேவையான கூற்றை நாங்கள் நிரூபித்துள்ளோம் எஃப் ஏபுள்ளி r இன் சில துளையிடப்பட்ட சுற்றுப்புறங்களில் இது உண்மையல்ல என்று இப்போது வைத்துக்கொள்வோம், அதாவது. புள்ளியின் தன்னிச்சையாக சிறிய துளையிடப்பட்ட சுற்றுப்புறத்தில் அத்தகைய புள்ளி உள்ளது ஜி",அந்த f(r") = A. பிறகு எதற்கும் பிதுளையிடப்பட்ட சுற்றுப்புறத்தில் 0 f(z u) = L. எனவே, தேவையான கூற்று உண்மை பி-யூயோ

எல்லா சந்தர்ப்பங்களிலும், மற்றும் தேற்றம் 26.7 நிரூபிக்கப்பட்டுள்ளது.

(சோகோட்ஸ்கியின்) தேற்றம் 26.7 இன் படி, எந்த ஒரு (தன்னிச்சையாக சிறிய) துளையிடப்பட்ட சுற்றுப்புறத்தின் அடிப்படையில் ஒருமைப் புள்ளியின் செயல்பாடு f(r) நீட்டிக்கப்பட்ட சிக்கலான விமானம் C இல் உள்ள எந்த எண்ணுக்கும் தன்னிச்சையாக நெருங்கிய மதிப்புகளை எடுக்கும்.

தனிமைப்படுத்தப்பட்ட ஒருமை புள்ளிகளைப் படிக்க, அடிப்படை அடிப்படை செயல்பாடுகளின் நன்கு அறியப்பட்ட டெய்லர் விரிவாக்கங்கள் பெரும்பாலும் பயனுள்ளதாக இருக்கும்.

எடுத்துக்காட்டு 2G.8. செயல்பாட்டிற்கான ஒருமைப் புள்ளி zq = 0 வகையைத் தீர்மானிக்கவும்

தீர்க்கப்பட்டது மற்றும் e. டெய்லர் தொடரில் உள்ள எண் மற்றும் வகுப்பினை r இன் அதிகாரங்களில் விரிவுபடுத்துகிறோம் (22.11) 3 z rக்குப் பதிலாக 1ஐக் கழித்தால், நமக்குக் கிடைக்கும்

(22.12) ஐப் பயன்படுத்தி, வகுப்பின் விரிவாக்கத்தைப் பெறுகிறோம்:

இந்த விரிவாக்கங்களில் உள்ள தொடர்கள் முழு சிக்கலான விமானத்திலும் € ஒன்றிணைகின்றன. எங்களிடம் உள்ளது

மற்றும் /2(2) புள்ளியின் சுற்றுப்புறத்தில் ஒத்தவை zo = 0 (மற்றும் முழு விமானத்திலும் கூட) மற்றும் /2(20) எஃப் 0, பின்னர் h(z)புள்ளி gF 0 இன் சில சுற்றுப்புறங்களிலும் பகுப்பாய்வு ஆகும். முடிவு 26.4 இன் படி, புள்ளி Zo = 0 என்பது வரிசையின் துருவமாகும் N = 4.

II உதாரணம் 26.9. ஒரு செயல்பாட்டின் ஒருமைப் புள்ளிகளைக் கண்டறியவும் f(z)= sin j - மற்றும் அவற்றின் வகையை தீர்மானிக்கவும்.

e மற்றும் e இல் P e. செயல்பாடு ஒற்றை இறுதி ஒருமை புள்ளியைக் கொண்டுள்ளது zq = 1. C இலிருந்து மற்ற புள்ளிகளில், செயல்பாடு w =--- பகுப்பாய்வு; எனவே பாவம் செயல்பாடு டபிள்யூபகுப்பாய்வாக இருக்கும்.

சைனின் விரிவாக்கத்தில் மாற்றீடு (22.12) - r க்கு பதிலாக, நாம் பெறுகிறோம்

20 = 1 புள்ளியின் துளையிடப்பட்ட சுற்றுப்புறத்தில் உள்ள லாரன்ட் தொடரில் பாவச் செயல்பாட்டின் விரிவாக்கத்தை நாங்கள் பெற்றுள்ளோம். இதன் விளைவாக வரும் விரிவாக்கமானது எதிர்மறை சக்திகளுடன் (r - 1) எண்ணற்ற சொற்களைக் கொண்டிருப்பதால், பின்னர் zq = 1 என்பது இன்றியமையாத ஒருமைப் புள்ளியாகும் (இந்த வழக்கில், லாரன்ட் விரிவாக்கம் முக்கிய பகுதியை மட்டுமே கொண்டுள்ளது, மேலும் சரியான பகுதி காணவில்லை).

இந்த வழக்கில் தொடர் விரிவாக்கத்தை நாடாமல், வரையறையில் இருந்து நேரடியாக ஒருமையின் தன்மையை நிறுவுவதும் சாத்தியம் என்பதை நினைவில் கொள்ளவும். உண்மையில், வரிசைகள் (r") மற்றும் (2") உடன் இணைகின்றன zo= 1, மற்றும் அது போன்ற f(z" n)= 1, /(2") = 0 (அத்தகைய தொடர்களை நீங்களே குறிப்பிடவும்) எனவே, f(z)எப்போது வரம்பு இல்லை z -> 1 மற்றும் எனவே புள்ளி zq - 1 அடிப்படையில் ஒருமை.

ஒரு புள்ளியின் சுற்றுப்புறத்தில் ஒரு செயல்பாட்டின் லாரன்ட் விரிவாக்கத்தின் கருத்தை அறிமுகப்படுத்துவோம் Zq = 00 மற்றும் இந்த இடத்தில் ஒருமையின் விரிவாக்கத்திற்கும் தன்மைக்கும் இடையே உள்ள தொடர்பைக் கருத்தில் கொள்ளுங்கள். ஒரு தனிமைப்படுத்தப்பட்ட ஒருமைப் புள்ளியின் வரையறைகள் மற்றும் அதன் வகை (அகற்றக்கூடியது, துருவம் அல்லது அடிப்படையில் ஒருமை) வழக்கிற்குச் செல்லும் என்பதை நினைவில் கொள்க. zq = oc மாறாமல். ஆனால் கோட்பாடுகள் 26.2. லாரன்ட் விரிவாக்கங்களின் தன்மையுடன் தொடர்புடைய 26.3 மற்றும் 26.6 ஆகியவை மாற்றப்பட வேண்டும். உறுப்பினர்கள் என்பதுதான் விஷயம் c n (z - 2o) ப. பி= -1,-2,..., முக்கிய பகுதி, இறுதிப் புள்ளிக்கு அருகில் உள்ள செயல்பாட்டின் "'ஒழுங்கற்ற தன்மையை" வரையறுக்கிறது Zq. மாறாக, உறுப்பினர்களுடன் வழக்கமான பகுதி பி= 1,2,... oo முனையும்; அவை ஒருமையின் தன்மையை தீர்மானிக்கின்றன Zq = oo. எனவே, oo வின் சுற்றுப்புறத்தில் விரிவாக்கத்தின் முக்கிய பகுதி நேர்மறை சக்திகளைக் கொண்ட விதிமுறைகளாக இருக்கும் பி,மற்றும் சரி - எதிர்மறையுடன்.

ஒரு புதிய மாறியை அறிமுகப்படுத்துவோம் w = 12. செயல்பாடு டிவி = 1/2, நீட்டிக்கப்பட்டதால் u(oo) = 0, ஒன்றுக்கு ஒன்று மற்றும் சுற்றுப்புறத்தை இணக்கமாக வரைபடமாக்குகிறது z > ஆர்புள்ளிகள் zq = 00 அருகில் |w| wq = 0. செயல்பாடு என்றால் f(z)ஒரு துளையிடப்பட்ட சுற்றுப்புறத்தில் பகுப்பாய்வு ஆர் z Zq = oc, பின்னர் செயல்பாடு G(w) = f(l/w)மஞ்சள் சுற்றுப்புறத்தில் பகுப்பாய்வு இருக்கும் 0 wo = 0. 2 -> oo இருக்கும் என்பதால் டபிள்யூ-> 0, பின்னர்

அதனால் தான் ஜி(வ)புள்ளியில் உள்ளது wq = 0 என்பது அதே வகையின் ஒருமையாகும் f(z)புள்ளியில் Zq = 00. wo = 0 என்ற புள்ளியின் துளையிடப்பட்ட சுற்றுப்புறத்தில் லாரன்ட் தொடரில் G(w) செயல்பாட்டை விரிவாக்குவோம்:

(26.5) இன் வலது பக்கத்தில் உள்ள தொகைகள் முறையே விரிவாக்கத்தின் சரியான மற்றும் முக்கிய பகுதிகளைக் குறிக்கின்றன. மாறி மாறி செல்லலாம் z,மாற்றுதல் w = 1/z:

குறிக்கும் பி\u003d -A *, 6 * \u003d 6_ " \u003d p உடன்மற்றும் அதை கவனிக்கிறேன் G(l/z) = f(z), நாங்கள் பெறுகிறோம்

சிதைவு (2G.G) என்று அழைக்கப்படுகிறது zq புள்ளியின் துளையிடப்பட்ட சுற்றுப்புறத்தில் f(z) செயல்பாட்டின் லாரன்ட் விரிவாக்கம்= ஓ. (2G.6) இன் முதல் தொகை அழைக்கப்படுகிறது வலது பகுதி, மற்றும் இரண்டாவது தொகை முக்கிய பாகம்இந்த சிதைவு. இந்த தொகைகள் விரிவாக்கத்தின் (26.5) சரியான மற்றும் முக்கிய பகுதிகளுடன் ஒத்துப்போவதால், விரிவாக்கம் (26.6) தேற்றங்கள் 26.2, 26.3 மற்றும் 26.6 ஆகியவற்றின் ஒப்புமைகளை பூர்த்தி செய்கிறது. எனவே, பின்வரும் தேற்றம் தேற்றம் 26.2 இன் அனலாக் ஆகும்.

தேற்றம் 26.10. தனிமைப்படுத்தப்பட்ட ஒற்றை புள்ளிZq - os (செயல்பாடுகள்/(ஜி) இந்த புள்ளியின் துளையிடப்பட்ட சுற்றுப்புறத்தில் உள்ள லாரன்ட் விரிவாக்கம் வடிவம் இருந்தால் மட்டுமே நீக்கக்கூடியது

டி.எஸ். சரியான பகுதியை மட்டுமே கொண்டுள்ளது.

நாங்கள் /(oo) = போடுகிறோம் இணைதொடர் (26.7) மூலம் வரையறுக்கப்பட்ட செயல்பாடு அக்கம்பக்கத்தில் ஒன்றிணைகிறது z > ஆர்புள்ளிகள் 2o \u003d oc, அழைக்கப்படுகிறது z புள்ளியில் பகுப்பாய்வு o = oo. (இந்த வரையறை செயல்பாட்டின் பகுப்பாய்விற்கு சமம் என்பதை நினைவில் கொள்க ஜி(வ) புள்ளியில் wo = 0.)

எடுத்துக்காட்டு 26.11. செயல்பாட்டின் zq = oo என்ற ஒற்றைப் புள்ளியை ஆராயவும்

வரம்பு வரையறுக்கப்பட்டதாக இருப்பதால், பிறகு zo = oo என்பது f(r) செயல்பாட்டின் நீக்கக்கூடிய ஒற்றைப் புள்ளியாகும். /(oo) = லிம் என்று போட்டால் J(z)= 0, பின்னர் f(z)ஆகிவிடும்

புள்ளியில் நடுக்கம் ஜோ= os. தொடர்புடைய விரிவாக்கத்தை எவ்வாறு கண்டுபிடிப்பது என்பதைக் காண்பிப்போம் (26.7). மாறி மாறி செல்லலாம் டபிள்யூ = 1 fz.மாற்றுதல் z= 1 /?e, நாம் பெறுகிறோம்

(கடைசி சமத்துவம் ww = 0 புள்ளியின் துளையிடப்பட்ட சுற்றுப்புறத்தில் செல்லுபடியாகும், ஆனால் நாம் வரையறையை (7(0) = 0) நீட்டிப்போம். இதன் விளைவாக வரும் செயல்பாடு ஒருமை புள்ளிகளைக் கொண்டுள்ளது w =±i, w =-1/3, மற்றும் புள்ளியில் Wq = 0 என்பது பகுப்பாய்வு ஆகும். விரிவாக்கும் செயல்பாடு ஜி(வ)டிகிரி மூலம் டபிள்யூ(எடுத்துக்காட்டு 25.7 இல் செய்யப்பட்டதைப் போல) மற்றும் அதன் விளைவாக வரும் சக்தித் தொடரில் மாற்றியமைத்தல் w = 1/zசெயல்பாட்டின் விரிவாக்கத்தை (26.7) பெறலாம் f(z)

வழக்குக்கான தேற்றம் 26.3 zo= oo பின்வரும் வடிவத்தில் மீண்டும் எழுதப்படும்.

தேற்றம் 26.12. தனிமைப்படுத்தப்பட்ட ஒற்றை புள்ளிசெல் = OS லாரன்ட் விரிவாக்கத்தின் முக்கிய பகுதியாக இருந்தால் மட்டுமே f(z) செயல்பாடு ஒரு துருவமாகும் (26.6) பூஜ்ஜியமற்ற குணகங்களின் வரையறுக்கப்பட்ட எண்ணிக்கையை மட்டுமே கொண்டுள்ளதுஉடன்":

இங்கே தொடர் என்பது வழக்கமான பகுதியாகும், மேலும் அடைப்புக்குறியிடப்பட்ட பல்லுறுப்புக்கோவை விரிவாக்கத்தின் முக்கிய பகுதியாகும். oc இல் உள்ள துருவத்தின் பெருக்கம் துருவத்தின் பெருக்கமாக வரையறுக்கப்படுகிறது wq = 0 செயல்பாடுகள் G(z)துருவத்தின் பெருக்கம் எண்ணுடன் ஒத்துப்போவதை எளிதாகக் காணலாம் என்இல் (26.8).

கே ப | (i 2 + 1) (z + 3) 2

ஒரு பணி. செயல்பாட்டைக் காட்டு f(z) =-- -- உள்ளது

புள்ளி zo =ஓ துருவ ஒழுங்கு 3.

ஒரு அத்தியாவசிய ஒற்றைப் புள்ளியில் தேற்றம் 26.6 வழக்குக்காக மீண்டும் எழுதப்பட்டது zo= os ஏறக்குறைய சொற்களஞ்சியம், மற்றும் நாங்கள் அதை விரிவாகக் குறிப்பிடவில்லை.

அடிப்படை கருத்துக்கள் மற்றும் வரையறைகள்:

பகுப்பாய்வு செயல்பாட்டின் பூஜ்ஜியம் f(z) என்பது "a" புள்ளியாகும், இதற்கு f(a)=0.

f(z) செயல்பாட்டின் "n" வரிசையின் பூஜ்ஜியம் "a" என்றால் fn(a)¹0 ஆகும்.

ஒரு ஒற்றைப் புள்ளி "a" ஆனது f(z) செயல்பாட்டின் தனிமைப்படுத்தப்பட்ட ஒருமைப் புள்ளி எனப்படும், "a" ஐத் தவிர வேறு ஒருமைப் புள்ளிகள் இல்லாத இந்தப் புள்ளியின் அருகில் இருந்தால்.

தனிமைப்படுத்தப்பட்ட ஒற்றை புள்ளிகள் மூன்று வகைகளாகும்:

1 நீக்கக்கூடிய சிறப்பு புள்ளிகள்;

3 அத்தியாவசிய ஒற்றை புள்ளிகள்.

கண்டுபிடிக்கப்பட்ட ஒருமைப் புள்ளியில் கொடுக்கப்பட்ட செயல்பாட்டின் நடத்தையின் அடிப்படையிலும், கண்டுபிடிக்கப்பட்ட ஒருமைப் புள்ளியின் அருகில் உள்ள செயல்பாட்டிற்காகப் பெறப்பட்ட லாரன்ட் தொடரின் வடிவத்தின் அடிப்படையிலும் ஒரு ஒற்றைப் புள்ளியின் வகையை தீர்மானிக்க முடியும்.

ஒரு ஒற்றை புள்ளியின் வகையை அதில் உள்ள செயல்பாட்டின் நடத்தை மூலம் தீர்மானித்தல்.

1. நீக்கக்கூடிய ஒற்றை புள்ளிகள்.

f(z) செயல்பாட்டின் தனிமைப்படுத்தப்பட்ட ஒருமை புள்ளி a வரையறுக்கப்பட்ட வரம்பு இருந்தால் நீக்கக்கூடியது என்று அழைக்கப்படுகிறது.

2. துருவங்கள்.

f(z) செயல்பாட்டின் தனிமைப்படுத்தப்பட்ட ஒருமை புள்ளி a துருவம் எனப்படும் .

3. குறிப்பிடத்தக்க ஒற்றை புள்ளிகள்.

f(z) செயல்பாட்டின் ஒரு தனிமைப்படுத்தப்பட்ட ஒருமைப் புள்ளி, வரையறுக்கப்பட்ட அல்லது எல்லையற்றதாக இல்லாவிட்டால், அத்தியாவசிய ஒருமைப் புள்ளி என்று அழைக்கப்படுகிறது.

செயல்பாட்டின் பூஜ்ஜியங்களுக்கும் துருவங்களுக்கும் இடையே பின்வரும் தொடர்பு நடைபெறுகிறது.

ஒரு புள்ளி a ஆனது f(Z) செயல்பாட்டின் n வரிசையின் துருவமாக இருக்க, இந்த புள்ளியானது செயல்பாட்டிற்கு n வரிசையின் பூஜ்ஜியமாக இருப்பது அவசியம் மற்றும் போதுமானது.

n=1 எனில் துருவமானது எளிமையானது எனப்படும்.

வரையறை:ஒற்றை மதிப்புடைய எழுத்தின் தனிமைப்படுத்தப்பட்ட ஒற்றைப் புள்ளி அழைக்கப்படுகிறது:

a) சிதைவின் முக்கிய பகுதி இல்லாவிட்டால் நீக்கக்கூடியது;

b) முக்கிய பகுதியில் வரையறுக்கப்பட்ட எண்ணிக்கையிலான உறுப்பினர்கள் இருந்தால் ஒரு கம்பம்;

c) முக்கிய பகுதி எண்ணற்ற சொற்களைக் கொண்டிருந்தால், அடிப்படையில் ஒருமைப் புள்ளி.

a) எனவே, நீக்கக்கூடிய ஒருமைப் புள்ளியின் சுற்றுப்புறத்தில், விரிவாக்கம் வடிவம் கொண்டது:

இது வட்டத்தின் அனைத்து புள்ளிகளிலும் செயல்பாட்டை வெளிப்படுத்துகிறது |z-a|

மையத்தில் z=a, சமத்துவம் தவறானது, ஏனெனில் z=a இல் உள்ள செயல்பாடு ஒரு இடைநிறுத்தத்தைக் கொண்டுள்ளது, மேலும் வலது பக்கம் தொடர்ச்சியாக இருக்கும். மையத்தில் உள்ள செயல்பாட்டின் மதிப்பு மாற்றப்பட்டால், அதை வலது பக்கத்தின் மதிப்புக்கு சமமாக எடுத்துக் கொண்டால், இடைவெளி அகற்றப்படும் - எனவே பெயர் - நீக்கக்கூடியது.

b) m வரிசையின் துருவத்தின் அருகில், Laurent தொடர் விரிவாக்கம் வடிவம் கொண்டது:

c) ஒரு எளிய கம்பத்தின் அருகில்

அவற்றின் கணக்கீட்டிற்கான விலக்குகள் மற்றும் சூத்திரங்கள்.

ஒரு தனிமைப்படுத்தப்பட்ட ஒருமைப் புள்ளி z 0 இல் உள்ள ஒரு பகுப்பாய்வுச் செயல்பாட்டின் எச்சம் f(z) என்பது ஒருங்கிணைப்பின் மதிப்புக்கு சமமான ஒரு கலப்பு எண்ணாகும். , z 0 என்ற புள்ளியை மையமாகக் கொண்ட வட்டம் L உடன் நேர்மறை திசையில் எடுக்கப்பட்டது, இது f(z) செயல்பாட்டின் பகுப்பாய்வு பகுதியில் உள்ளது (அதாவது, வளையம் 0 இல்<|z-z0|

தனிமைப்படுத்தப்பட்ட ஒருமைப் புள்ளி z 0 இல் உள்ள f(z) செயல்பாட்டின் எச்சம் Res f(z 0) அல்லது Res (f(z); z 0) என்ற குறியீட்டால் குறிக்கப்படுகிறது. இந்த வழியில்,

Resf(z0)= . (22.15.1)

சூத்திரத்தில் (22.15.1) n=-1 ஐ வைத்தால், நாம் பெறுவோம்:

C-1=

அல்லது Res f(z 0)= C -1 ,

அந்த. z 0 என்ற ஒற்றைப் புள்ளியைப் பொறுத்து f(z) செயல்பாட்டின் எச்சம், லாரன்ட் தொடரில் f(z) செயல்பாட்டின் விரிவாக்கத்தில் எதிர்மறை அடுக்குடன் கூடிய முதல் காலத்தின் குணகத்திற்குச் சமம்.

விலக்குகளின் கணக்கீடு.

வழக்கமான அல்லது நீக்கக்கூடிய ஒற்றை புள்ளிகள். வெளிப்படையாக, z=z 0 என்பது f(z) செயல்பாட்டின் வழக்கமான அல்லது நீக்கக்கூடிய ஒற்றைப் புள்ளியாக இருந்தால், Res f(z 0)=0 (இந்த நிகழ்வுகளில் Laurent சிதைவில் முக்கியப் பகுதி இல்லை, எனவே c-1= 0)

துருவம். புள்ளி z 0 என்பது f(z) செயல்பாட்டின் எளிய துருவமாக இருக்கட்டும். பின்னர் z 0 புள்ளியின் அருகில் உள்ள f(z) செயல்பாட்டிற்கான லாரன்ட் தொடர் வடிவம் கொண்டது:

இங்கிருந்து

எனவே, இந்த சமத்துவத்தை z --z 0 என வரம்பிற்குள் கடந்து, நாம் பெறுகிறோம்

Res f(z0)=

அடிப்படையில் சிறப்பு புள்ளி. புள்ளி z 0 என்பது f(z) செயல்பாட்டின் அடிப்படையில் ஒருமைப் புள்ளியாக இருந்தால், இந்த கட்டத்தில் செயல்பாட்டின் எச்சத்தைக் கணக்கிட, ஒரு லாரன்ட் தொடரில் செயல்பாட்டின் விரிவாக்கத்தில் குணகம் c-1 ஐ நேரடியாகத் தீர்மானிக்கிறது.

நிகழ்வு வகைப்பாடு. தொகை, நிகழ்வுகளின் தயாரிப்பு, அவற்றின் பண்புகள், வரைகலை பிரதிநிதித்துவம்.

நிகழ்வுகள் பிரிக்கப்பட்டுள்ளன:

1. சீரற்ற

2. நம்பகத்தன்மை

3. சாத்தியமற்றது

நம்பகமான - இது இந்த நிலைமைகளில் அவசியமாக நிகழும் ஒரு நிகழ்வு (இரவைத் தொடர்ந்து காலை).

ரேண்டம் என்பது நிகழக்கூடிய அல்லது நிகழாத ஒரு நிகழ்வு (தேர்வில் தேர்ச்சி பெறுதல்).

சாத்தியமற்றது என்பது கொடுக்கப்பட்ட நிபந்தனைகளின் கீழ் நிகழாத ஒரு நிகழ்வாகும் (பெட்டியிலிருந்து ஒரு பச்சை பென்சிலை மட்டும் சிவப்பு நிறத்துடன் எடுத்துக் கொள்ளுங்கள்).