Тусгаарлагдсан ганц цэгүүд. Тусгаарлагдсан ганц цэгүүд, тэдгээрийн ангилал

Тодорхойлолт.Функцийн онцгой цэгийг дуудна тусгаарлагдсан, хэрэв энэ цэгийн зарим хэсэгт аналитик функц (өөрөөр хэлбэл цагираг дахь аналитик) байгаа бол.

Функцийн тусгаарлагдсан ганц цэгүүдийг ангилах нь энэ функцийн нэг цэгийн ойролцоох үйл ажиллагаатай холбоотой.

Тодорхойлолт.цэг гэж нэрлэдэг нэг удаагийн -д энэ функцийн хязгаарлагдмал хязгаар байгаа бол функцийн ганц цэг.

Жишээ 5Функц нь цэг дээр зөөврийн онцгой шинж чанартай болохыг харуул.

Шийдэл.Эхний гайхалтай хязгаарыг эргэн санахад бид тооцоолно

Энэ нь өгөгдсөн функц нь цэг дээр зөөврийн онцгой шинж чанартай байна гэсэн үг юм.

Даалгавар 4.Цэг нь салгаж болно гэдгийг харуул.

Тодорхойлолт.цэг гэж нэрлэдэг туйл функц , хэрэв энэ функц нь тодорхойгүй хугацаагаар нэмэгддэг бол тэр нь .

Аналитик функцийн тэг ба туйл гэсэн ойлголтуудын уялдаа холбоог анхаарч үзье. Функцийг -ээр төлөөлүүлье.

Хэрэв цэг нь функцийн энгийн тэг бол функц нь энгийн туйлтай байна

Хэрэв цэг нь функцийн хувьд тэг эрэмбээр байвал функцийн хувьд туйл болно захиалга.

Жишээ 6Функц нь цэг дээр 3-р эрэмбийн туйлтай болохыг харуул.

Шийдэл.Бид авдаг гэж бодвол. Бид тэглэх хандлагатай байдаг тул ямар ч хуулийн дагуу . Дараа нь , мөн түүнтэй хамт функц нь өөрөө тодорхойгүй хугацаагаар нэмэгддэг. Тиймээс, , өөрөөр хэлбэл, ганц цэг нь туйл юм. Функцийн хувьд энэ цэг нь гурав дахин тэг байх нь ойлгомжтой. Тиймээс, энэ функцийн хувьд цэг нь гуравдугаар эрэмбийн туйл юм.

Даалгавар 5.Цэг нь энгийн туйлтай болохыг харуул.

Тодорхойлолт.цэг гэж нэрлэдэг үндсэндээ онцгой функцийн цэг, хэрэв энэ цэгт функцийн төгсгөл ба төгсгөлгүй хязгаар байхгүй бол (функцийн зан төлөв тодорхойлогдоогүй).

Функцийн чухал ганц цэг байцгаая. Дараа нь аливаа урьдчилан өгөгдсөн комплекс тооны хувьд нийлдэг цэгүүдийн дараалал байдаг бөгөөд тэдгээрийн дагуу утгууд нь : ( Сочоккийн теорем).

Жишээ 7Нэг цэг дэх функц чухал онцгой шинж чанартай болохыг харуул.

Шийдэл.Тухайн цэгийн ойролцоох өгөгдсөн функцийн үйлдлийг авч үзье. Учир нь бодит тэнхлэгийн эерэг хэсгийн дагуу (өөрөөр хэлбэл ) бид ба ; хэрэв бодит тэнхлэгийн сөрөг хэсгийн дагуу (өөрөөр хэлбэл) байвал ба . Тиймээс ямар ч хязгаарлалт байхгүй. Тодорхойлолтоор бол функц нь нэг цэгт чухал онцгой шинж чанартай байдаг.

Сочоккийн теоремын үүднээс тэг дэх функцийн үйлдлийг авч үзье. Тэг болон хязгааргүйгээс өөр ямар ч комплекс тоо байг.

Тэгш байдлаас бид олдог. Бид цэгүүдийн дарааллыг олж авна гэж үзвэл , . Мэдээжийн хэрэг, . Энэ дарааллын цэг бүрт функц нь -тэй тэнцүү, тиймээс

Даалгавар 6.Функц нь нэг цэгт чухал онцгой шинж чанартай болохыг харуул.

Хязгааргүй цэгийг үргэлж функцийн хувьд онцгой гэж үздэг. Хэрэв уг функц нь эх дээр төвлөрсөн тойргийн гадна өөр ганц цэггүй бол тухайн цэгийг функцийн тусгаарлагдсан ганц цэг гэнэ.

Тусгаарлагдсан ганц цэгүүдийн ангиллыг мөн тохиолдлоор өргөжүүлж болно.

Жишээ 8Функц нь хязгааргүйд давхар туйлтай болохыг харуул.

Шийдэл.функцийг авч үзье , хаана нь цэгийн хөрш дэх аналитик функц ба . Энэ нь функц нь хязгааргүйд давхар тэгтэй, харин функцийн хувьд цэг нь давхар туйл байна гэсэн үг юм.

Жишээ 9Функц нь хязгааргүй чухал онцгой шинж чанартай болохыг харуул.

Шийдэл.Үүнтэй төстэй асуудлыг pr.7-д авч үзсэн болно. Хязгааргүй алслагдсан цэгийн ойролцоох функцийн үйлдлийг авч үзье. Бодит тэнхлэгийн эерэг хэсгийн дагуу, бодит тэнхлэгийн сөрөг хэсгийн дагуу. Энэ нь тухайн цэг дээр функцийн хязгаар байхгүй гэсэн үг бөгөөд тодорхойлолтын дагуу энэ цэг нь үндсэндээ ганц байдаг.

Нэг цэг дэх функцийн онцгой байдлын мөн чанарыг эндээс дүгнэж болно гол хэсэг Энэ цэгийн ойролцоох Лорент өргөтгөл.

Теорем 1.Үүний тулд нэг удаагийн функцийн ганц цэг , энэ нь шаардлагатай бөгөөд хангалттай юм харгалзах Лорент өргөтгөл үндсэн хэсгийг агуулаагүй.

Даалгавар 6.Функцийг цэгийн ойролцоох Тейлорын өргөтгөлийг ашигласнаар энэ нь тэг дээр зөөврийн онцгой шинж чанартай болохыг харуул.

Теорем 2.Үүний тулд туйл чиг үүрэг , шаардлагатай бөгөөд хангалттай учраас гол хэсэг холбогдох Лорентын өргөтгөл хязгаарлагдмал тооны гишүүдийг багтаасан :

Хамгийн их сөрөг нэр томъёоны тоо нь туйлын дарааллыг тодорхойлдог.

Энэ тохиолдолд функцийг дараах байдлаар илэрхийлж болно

цэгийн аналитик функц хаана байна, , туйлын дараалал.

Жишээ 10Функц нь цэгүүдэд энгийн туйлтай болохыг харуул.

Шийдэл.Нэг цэгийг авч үзье. Бид 2-р жишээнээс авсан энэ цэгийн ойролцоо энэ функцийн Лорентын өргөтгөлийг ашигладаг.

Энэ тэлэлтийн гол хэсгийн хамгийн өндөр (ба цорын ганц) сөрөг хүч нь нэгтэй тэнцүү тул цэг нь энэ функцийн энгийн туйл юм.

Энэ үр дүнг өөр аргаар олж авах боломжтой байсан. Бид хэлбэрээр төлөөлж, тавьж үзье - энэ нь цэг дээр аналитик функц юм. Тиймээс (8)-ын улмаас энэ функц цэг дээр энгийн туйлтай байна.

Өөр нэг арга: цэг дээр энгийн тэгтэй функцийг авч үзье. Тиймээс энэ үед энгийн шонтой байна.

Үүний нэгэн адил функцийг хэлбэрт бичвэл хаана нь цэг дээр функц аналитик байна, тэгвэл тухайн цэг нь функцийн энгийн туйл болох нь шууд тодорхой болно.

Даалгавар 7.Функц нь цэг дээр 2-р эрэмбийн туйл, цэг дээр 4-р зэрэглэлийн туйлтай болохыг харуул.

Теорем 3.Үүний тулд үндсэндээ онцгой функцийн цэг , энэ нь шаардлагатай бөгөөд хангалттай юм гол хэсэг цэгийн хөрш Лоран өргөтгөл хязгааргүй тооны гишүүдийг агуулж байв .

Жишээ 11.Функцийн цэг дээрх онцгой байдлын шинж чанарыг тодорхойлно уу

Шийдэл.Косинусын алдартай өргөтгөлийн оронд бид дараахь зүйлийг тавьдаг.

Тиймээс цэгийн ойролцоох Лорентын тэлэлт нь хэлбэртэй байна

Энд зөв хэсэг нь нэг нэр томъёо юм. Мөн үндсэн хэсэг нь хязгааргүй тооны нэр томъёог агуулдаг тул цэг нь үндсэндээ ганц юм.

Даалгавар 8.Тухайн үед функц чухал онцгой шинж чанартай болохыг харуул.

Зарим функцийг авч үзээд түүний Лорентын өргөтгөлийг дараах цэг дээр бич.

Цэг нь цэг рүүгээ орох хооронд орлуулъя. Одоо бид хязгааргүй цэгийн ойролцоо байна

Энэ нь шинэ тэмдэглэгээг нэвтрүүлэх хэвээр байна. Бид авдаг

гол хэсэг нь хаана байна, мөн хязгааргүй алслагдсан цэгийн ойролцоох функцын Лорентын өргөтгөлийн тогтмол хэсэг юм. Ийнхүү цэгийн хөрш дэх функцийг Лорентын өргөтгөлд гол хэсэг нь эерэг зэрэглэлийн цуваа, харин зөв хэсэг нь сөрөг түвшний цуваа байна. Үүнийг харгалзан үзээд

Гэсэн хэдий ч, онцгой байдлын мөн чанарыг тодорхойлох дээрх шалгуур нь хязгааргүй алслагдсан цэгийн хувьд хүчинтэй хэвээр байна.

Жишээ 12.Цэг дэх функцийн онцгой байдлын мөн чанарыг олж мэд. , дараа нь энэ нь нэг хэсэгтээ тусгаарлагдаагүй болж хувирах болно.

Жишээ 15Хязгааргүй алслагдсан цэг дэх функц нь чухал онцгой шинж чанартай байдаг. Функцийн цэг нь тусгаарлагдсан ганц цэг биш гэдгийг харуул.

Шийдэл.Функц нь хуваагчийн тэг дээр, өөрөөр хэлбэл , цэгүүдэд хязгааргүй олон туйлтай байна. Учир нь , тэгвэл аль ч хөршид шон байдаг цэг нь туйлуудын хязгаарын цэг юм.

Хоёр бие даасан дифференциал тэгшитгэлийн системээр тодорхойлсон загварууд.

фазын хавтгай. Үе шаттай хөрөг зураг. изоклин арга. гол изоклинууд. Тогтвортой байдлын тогтвортой байдал. Шугаман системүүд. Ганц цэгийн төрөл: зангилаа, эмээл, фокус, төв. Жишээ нь: нэгдүгээр эрэмбийн химийн урвалууд.

Биологийн системийн шинж чанаруудын чанарын загварчлалын талаархи хамгийн сонирхолтой үр дүнг хоёр дифференциал тэгшитгэлийн загварууд дээр авсан бөгөөд энэ нь аргыг ашиглан чанарын судалгаа хийх боломжийг олгодог. фазын хавтгай. Ерөнхий хэлбэрийн хоёр бие даасан энгийн дифференциал тэгшитгэлийн системийг авч үзье

(4.1)

P(x,y), Q(x,y)- зарим домэйнд тодорхойлогдсон тасралтгүй функцууд ГЕвклидийн хавтгай ( x,y- Декарт координатууд) ба энэ хэсэгт эхнийхээс багагүй дарааллын тасралтгүй деривативууд байна.

Бүс нутаг Гхязгааргүй эсвэл хязгаарлагдмал байж болно. Хэрэв хувьсагч x, yтодорхой биологийн утгатай (бодисын концентраци, зүйлийн элбэг дэлбэг байдал), ихэвчлэн газар нутаг Гбаруун хагас хавтгайн эерэг квадрат:

0 £ x< ¥ ,0 £ y< ¥ .

Бодисын агууламж эсвэл зүйлийн элбэг дэлбэг байдлыг дээрээс нь хөлөг онгоцны эзэлхүүн эсвэл амьдрах орчны талбайгаар хязгаарлаж болно. Дараа нь хувьсагчдын хүрээ нь дараах хэлбэртэй байна.

0 £ x< x 0 , 0 £ y< y 0 .

Хувьсагч x, yтэгшитгэлийн системийн дагуу цаг хугацааны өөрчлөлт (4.1), ингэснээр системийн төлөв бүр нь хувьсагчийн хос утгуудтай тохирч байх болно ( x, y).

Үүний эсрэгээр, хувьсагч бүрийн хувьд ( x, y) системийн тодорхой төлөвтэй тохирч байна.

Хувьсагчийн утгыг зурсан координатын тэнхлэг бүхий хавтгайг авч үзье x,y. Цэг бүр МЭнэ хавтгай нь системийн тодорхой төлөвтэй тохирч байна. Ийм хавтгайг фазын хавтгай гэж нэрлэдэг бөгөөд системийн бүх төлөвийн нийлбэрийг дүрсэлдэг. M(x, y) цэгийг дүрслэх буюу дүрслэх цэг гэнэ.

Цагийн эхний мөчид зөвшөөрнө үү t=t 0 цэгийн координатыг илэрхийлнэ М 0 (x(т 0),y(т 0)). Дараагийн мөч бүрт тдүрслэх цэг нь хувьсагчдын утгын өөрчлөлтийн дагуу шилжих болно x(т),y(т). Цэгүүдийн багц М(x(т), y(t)) фазын хавтгай дээр, байрлал нь цаг хугацааны явцад хувьсагчийг өөрчлөх явцад системийн төлөвтэй тохирч байна. x(t), y(t)тэгшитгэлийн дагуу (4.1) гэж нэрлэдэг фазын замнал.

Хувьсагчдын өөр өөр анхны утгуудын фазын траекторын багц нь системийн хялбар харагдах "хөрөг" -ийг өгдөг. Барилга үе шатны хөрөг зурагхувьсагчийн өөрчлөлтийн мөн чанарын талаар дүгнэлт хийх боломжийг танд олгоно x, yтэгшитгэлийн анхны системийн аналитик шийдлүүдийг мэдэхгүй(4.1).

Фазын хөрөг зургийг дүрслэхийн тулд фазын хавтгайн цэг бүрт системийн траекторийн чиглэлийн вектор талбарыг байгуулах шаардлагатай. Нэмэлтийг зааж өгснөөрД t>0,Бид зохих нэмэгдлийг авна Д xболон Д yилэрхийллээс:

Д x=P(x,y)Д т,

Д y=Q(x,y)Д т.

вектор чиглэл dy/dxцэг дээр ( x, y) функцүүдийн тэмдгээс хамаарна P(x, y), Q(x, y)мөн хүснэгтээр өгч болно:

P(x,y)>0,Q(x,y)>0
P(x,y)<0,Q(x,y)<0
P(x,y)>0,Q(x,y)<0
P(x,y)<0,Q(x,y)>0

.(4.2)

Энэ тэгшитгэлийн шийдэл y=y(x, c), эсвэл далд хэлбэрээр Ф(x,y)=c,хаана -тайнь интегралын тогтмол бөгөөд (4.2) тэгшитгэлийн интеграл муруйн бүлгийг өгдөг - фазын траекторуудсистем (4.1) онгоцонд x, y.

Изоклин арга

Фазын хөрөг зургийг бүтээхийн тулд ашигладаг изоклин арга -Интеграл муруйг тодорхой нэг өнцгөөр огтолж буй фазын хавтгай дээр шугамууд татагдана. Изоклин тэгшитгэлийг (4.2) -аас авахад хялбар байдаг. тавья

хаана ГЭХДЭЭ– тодорхой тогтмол. Утга ГЭХДЭЭфазын траекторийн шүргэгч налуугийн тангенсыг илэрхийлдэг ба -аас утгыг авч болно.¥ + руу ¥ . Оронд нь орлуулах dy/dx(4.2) дахь тоо хэмжээ ГЭХДЭЭБид изоклин тэгшитгэлийг олж авна.

.(4.3)

Тэгшитгэл (4.3) нь хавтгайн цэг бүрт тохирох интеграл муруйн цорын ганц шүргэгчийг тодорхойлно. P(x,y)= 0, Q (x,y) = 0 , үүсмэлийн утга тодорхойгүй болсон тул шүргэгчийн чиглэл тодорхойгүй болно:

.

Энэ цэг нь бүх изоклинуудын огтлолцох цэг юм - онцгой цэг.Энэ нь хувьсагчдын цаг хугацааны деривативуудыг нэгэн зэрэг арилгадаг xболон y.

Тиймээс ганц цэг дээр хувьсагчдын өөрчлөлтийн хурд тэгтэй тэнцүү байна. Иймд фазын траекторийн дифференциал тэгшитгэлийн онцгой цэг (4.2) нь дараахтай тохирч байна. системийн хөдөлгөөнгүй байдал(4.1) ба түүний координатууд нь хувьсагчдын суурин утгууд юм x, y.

Ялангуяа сонирхолтой байдаг Гол изоклинууд:

dy/dx=0, P(x,y)=0 – хэвтээ шүргэгчийн изоклин ба

dy/dx=¥ , Q(x,y)=0 – босоо шүргэгчийн изоклин.

Гол изоклиныг байгуулж, тэдгээрийн огтлолцлын цэгийг олох замаар (х, у), координатууд нь дараахь нөхцлийг хангасан байна.

Тиймээс бид фазын траекторийн шүргэлтийн чиглэл тодорхойгүй байх фазын хавтгайн бүх изоклинуудын огтлолцох цэгийг олох болно. Энэ нь - онцгой цэг, энэ нь тохирч байна системийн хөдөлгөөнгүй байдал(Зураг 4.2).

Систем (4.1) нь фазын хавтгай дээрх үндсэн изоклинуудын огтлолцох цэгүүдийн тоотой адил олон суурин төлөвтэй байна.

Фазын замнал бүр нь ижил төлөвөөр дамждаг динамик системийн хөдөлгөөний багцтай тохирч, зөвхөн цаг хугацааны лавлагааны эхэн үед бие биенээсээ ялгаатай.

Хэрэв Коши теоремын нөхцөл хангагдсан бол орон зайн цэг бүрээр дамжина x, y, tнэг интеграл муруйгаар дамждаг. Бие даасан байдлын ачаар фазын траекторийн хувьд ч мөн адил: фазын хавтгайн цэг бүрээр өвөрмөц фазын траектор дамждаг.

Тогтвортой байдлын тогтвортой байдал

Систем тэнцвэрт байдалд байг.

Дараа нь төлөөлөх цэг нь системийн цорын ганц цэгүүдийн аль нэгэнд байрладаг бөгөөд тодорхойлолтоор:

.

Ганц цэг тогтвортой байна уу, үгүй ​​юу гэдгийг төлөөлөх цэг нь хөдөлгөөнгүй байдлаас бага зэрэг хазайлттай гарах эсэхээр тодорхойлогддог. Хоёр тэгшитгэлийн системд хэрэглэснээр хэл дээрх тогтвортой байдлын тодорхойлолтд, гдараах байдлаар.

Тэнцвэрийн төлөвөөс хазайсан аль нэг хэсэгт тэнцвэрийн төлөв тогтвортой байна. (д )талбайг зааж өгч болно г (д ), тэнцвэрийн төлөвийг тойрсон, тухайн бүс нутгийн доторх замнал нь эхэлдэггүй шинж чанартай байдаг. г , хэзээ ч хил дээр хүрэхгүй д . (Зураг 4.4)

Том ангиллын системүүдийн хувьд - бүдүүлэг системүүд – тэгшитгэлийн төрлийг бага зэрэг өөрчлөхөд зан төлөвийн шинж чанар өөрчлөгддөггүй, суурин төлөвийн ойролцоох зан үйлийн хэлбэрийн талаарх мэдээллийг эх хувилбарыг биш харин хялбаршуулсан байдлыг судлах замаар олж авах боломжтой. шугаманжуулсансистем.

Шугаман системүүд.

Хоёр шугаман тэгшитгэлийн системийг авч үзье.

.(4.4)

Энд a B C D- тогтмол, x, y- Фазын хавтгай дээрх декартын координатууд.

Ерөнхий шийдлийг дараах хэлбэрээр хайх болно.

.(4.5)

Эдгээр илэрхийллийг (4.4)-д орлуулж, бууруул д л т:

(4.6)

Мэдэгдэхгүй алгебрийн тэгшитгэлийн систем (4.6). А, БҮл мэдэгдэхүүдийн коэффициентээс бүрдэх тодорхойлогч нь тэгтэй тэнцүү байвал л тэгээс өөр шийдэлтэй байна.

.

Энэ тодорхойлогчийг өргөжүүлснээр бид системийн шинж чанарын тэгшитгэлийг олж авна.

.(4.7)

Энэ тэгшитгэлийн шийдэл нь индикаторын утгыг өгдөгл 1,2 , үүний доор тэгээс өөр утгыг авах боломжтой Аболон Б(4.6) тэгшитгэлийн шийдлүүд. Эдгээр үнэт зүйлс нь

.(4.8)

Хэрэв радикал илэрхийлэл сөрөг байвалл 1,2 нийлмэл нийлмэл тоо. (4.7) тэгшитгэлийн язгуур хоёулаа тэгээс өөр бодит хэсгүүдтэй, олон үндэс байхгүй гэж үзье. Дараа нь (4.4) системийн ерөнхий шийдийг илтгэгчтэй индексийн шугаман хослолоор дүрсэлж болно.л 1 , л 2 :

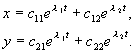(4.9)

Фазын хавтгай дээрх системийн боломжит траекторийн шинж чанарыг шинжлэхийн тулд бид ашигладаг шугаман нэгэн төрлийн координатын хувиргалт,энэ нь системийг авчрах болно каноник хэлбэр:

,(4.10)

Энэ нь анхны системтэй харьцуулахад фазын хавтгайд илүү тохиромжтой дүрслэлийг зөвшөөрдөг (4.4). Шинэ координатуудыг танилцуулъяξ , η томъёоны дагуу:

(4.1)

Бодит хэсгүүд нь тэгтэй тэнцүү биш бол шугаман алгебрийн хичээлээс мэдэгдэж байнал 1 , л 2 Анхны системийг (4.4) хувиргалтуудын тусламжтайгаар (4.11) үргэлж каноник хэлбэрт (4.10) хувиргаж, фазын хавтгай дээрх зан төлөвийг судлах боломжтой.ξ , η . Энд гарч ирж болох янз бүрийн тохиолдлуудыг авч үзье.

Үндэс λ 1 , λ 2 - хүчинтэй, ижил тэмдэгтэй

Энэ тохиолдолд хувиргах коэффициентүүд нь бодит, бид бодит хавтгайгаас хөдөлдөгx,yбодит хавтгайд ξ, η. (4.10) тэгшитгэлийн хоёр дахь хэсгийг эхнийх нь хувааснаар бид олж авна:

.(4.12)

Энэ тэгшитгэлийг нэгтгэснээр бид олдог:

Хаана.(4.13)

λ гэж ойлгохыг зөвшөөрье 2 том модуль бүхий шинж чанарын тэгшитгэлийн үндэс нь бидний үндэслэлийн ерөнхий байдлыг зөрчөөгүй. Дараа нь авч үзэх тохиолдолд үндэс λ байна 1 , λ2 - хүчинтэй, ижил тэмдэгтэй,а>1 , мөн бид параболик төрлийн интеграл муруйг авч үзэж байна.

Бүх салшгүй муруй (тэнхлэгээс бусад η , энэ нь тохирч байна ) тэнхлэгийн эхэнд хүрэх ξ, Энэ нь мөн (4.11) тэгшитгэлийн интеграл муруй юм. Координатын гарал үүсэл нь онцгой цэг юм.

Одоо фазын траекторийн дагуу дүрслэх цэгийн хөдөлгөөний чиглэлийг олж мэдье. Хэрэв λ 1 , λ 2 сөрөг байвал (4.10), |ξ|, |η| тэгшитгэлээс харж болно. цаг хугацааны явцад буурах. Төлөөлөх цэг нь гарал үүслийн цэг рүү ойртдог боловч хэзээ ч хүрч чаддаггүй. Үгүй бол энэ нь фазын хавтгайн цэг бүрээр зөвхөн нэг фазын траектор дамждаг гэсэн Кошигийн теоремтой зөрчилдөх болно.

Яг л параболын гэр бүл шиг интеграл муруй дамждаг ийм онцгой цэг гарал үүслээр дамждаг, зангилаа гэж нэрлэдэг (Зураг 1). 4.5)

λ дахь зангилааны төрлийн тэнцвэрийн төлөв 1 , λ 2 < 0 Ляпуновын хэлснээр энэ нь тогтвортой байна, учир нь төлөөлөх цэг нь бүх интеграл муруй дагуу координатын эхлэл рүү шилждэг. тэр тогтвортой зангилаа. Хэрэв λ 1 , λ 2 > 0, тэгвэл |ξ|, |η| цаг хугацаа өнгөрөх тусам нэмэгдэж, төлөөлөх цэг нь эхээс холддог. Энэ тохиолдолд онцгой цэг– тогтворгүй зангилаа .

Фазын хавтгай дээр x, y интеграл муруйнуудын зан байдлын ерөнхий чанарын шинж чанар хэвээр байх боловч интеграл муруйнуудын шүргэгч координатын тэнхлэгүүдтэй давхцахгүй. Эдгээр шүргэгчийн налуу өнцгийг коэффициентүүдийн харьцаагаар тодорхойлно α , β , γ , δ тэгшитгэлд (4.11).

Үндэс λ 1 , λ 2 хүчинтэй бөгөөд өөр өөр шинж тэмдэгтэй.

-аас хөрвүүлэхкоординатууд x,y координатууд ξ, η дахин бодит. Каноник хувьсагчдын тэгшитгэлүүд дахин (4.10) хэлбэртэй болсон боловч одоо λ тэмдэгтүүд байна. 1 , λ 2 өөр. Фазын траекторийн тэгшитгэл нь хэлбэртэй байна:

Хаана, (4.14)

(4.14) нэгтгэснээр бид олдог

(4.15)

тэр тэгшитгэл нь хоёр координат тэнхлэгт гиперболын төрлийн муруйн бүлгийг тодорхойлдогасимптотууд ( at а=1 Бид хоёр талт гиперболын гэр бүлтэй болно). Энэ тохиолдолд координатын тэнхлэгүүд нь мөн салшгүй муруй болно– Эдгээр нь гарал үүслээр дамждаг цорын ганц интеграл муруй байх болно. Тус бүрүүнээс гурван фазын замналаас бүрдэнэ: тэнцвэрийн төлөв рүү (эсвэл тэнцвэрийн төлөвөөс хол) болон тэнцвэрийн төлөв рүү чиглэсэн хоёр хөдөлгөөний. Бусад бүх интеграл муруйнууд– нь гарал үүслээр дамждаггүй гиперболууд юм (Зураг 1). 4.6) Энэ онцгой цэгийг нэрлэдэг "эмээл ». Уулын эмээлийн ойролцоох түвшний шугамууд нь эмээлийн эргэн тойронд фазын траекторууд шиг ажилладаг.

Тэнцвэрийн төлөвийн ойролцоо фазын траекторын дагуу төлөөлөх цэгийн хөдөлгөөний мөн чанарыг авч үзье. Жишээлбэл,λ 1 >0 , λ 2<0 . Дараа нь төлөөлөх цэгийг тэнхлэгт байрлуулна ξ , гарал үүслээс холдож, тэнхлэгт байрлуулна η – координатын гарал үүсэлд хязгааргүй ойртох болно, хязгаарлагдмал хугацаанд хүрэхгүйгээр. Анхны агшинд төлөөлөх цэг хаана ч байсан (ганц цэг болон асимптот дээрх цэгүүдийг эс тооцвол) η =0), Эхэндээ интеграл муруйнуудын аль нэгийг дагуулан ганц цэг рүү шилжсэн ч эцэст нь тэнцвэрийн төлөвөөс холдох болно..

Энэ нь ойлгомжтой эмээлийн төрлийн ганц цэг нь үргэлж тогтворгүй байдаг . Зөвхөн асимптот дээр тусгайлан сонгосон анхны нөхцөлдη =0 систем тэнцвэрт байдалд ойртоно. Гэсэн хэдий ч энэ нь систем тогтворгүй гэсэн мэдэгдэлтэй зөрчилддөггүй. Хэрэв бид тооцвол, фазын хавтгай дээрх системийн бүх анхны төлөв ижил магадлалтай бол тухайн чиглэлийн хөдөлгөөнд тохирсон анхны төлөвийн магадлал.руу ганц цэг нь тэгтэй тэнцүү байна. Тиймээс аливаа бодит хөдөлгөөн нь системийг тэнцвэрт байдлаас гаргах болно.Координат руу буцахx,y,Бид гарал үүслийн эргэн тойронд траекторийн хөдөлгөөний мөн чанарын ижил төстэй дүр зургийг олж авдаг.

Зангилаа ба эмээлийн авч үзсэн тохиолдлуудын хоорондох зааг нь ийм байнахэзээ онцлог үзүүлэлтүүдийн нэг, жишээ нь λ 1 , алга болдог бөгөөд энэ нь системийн тодорхойлогч үед үүсдэг- илэрхийлэл adbc=0(4.8 томъёог үзнэ үү ). Энэ тохиолдолд (4.4) тэгшитгэлийн баруун талын коэффициентүүд хоорондоо пропорциональ байна.:

систем нь тэнцвэрт байдлын хувьд шугамын бүх цэгүүдийг илэрхийлдэг:

Үлдсэн интеграл муруйнууд нь налуутай зэрэгцээ шугамуудын гэр бүл юм , λ шинж чанарын тэгшитгэлийн хоёр дахь язгуурын тэмдгээс хамааран төлөөлөх цэгүүд тэнцвэрийн төлөвт ойртох эсвэл түүнээс холдох болно. 2 = a+d.(Зураг 4. 7 ) Энэ тохиолдолд тэнцвэрт байдлын координат нь хувьсагчдын анхны утгаас хамаарна.

Үндэс λ 1 , λ 2 – цогцолборконьюгат

Энэ тохиолдолд бодит байдал дээрxболон yбид ... болно нарийн төвөгтэй коньюгатуудтай ξ , η (4.10) . Гэсэн хэдий ч, өөр нэг завсрын хувиргалт хийснээр энэ тохиолдолд бодит шугаман нэгэн төрлийн хувиргалтыг багасгах боломжтой. тавья:

(4.16)

хаана а, б,болон у, v – бодит үнэ цэнэ. -аас хувирсныг харуулж болноx,yруу у, v бидний таамаглалаар бол бодит, шугаман, тэгээс өөр тодорхойлогчтой нэгэн төрлийн байна. Тэгшитгэлийн улмаас(4.10, 4.16) бидэнд:

хаана

(4.17)

Тэгшитгэлийн хоёр дахь хэсгийг эхнийх нь хуваах, бид авах:

аль нь нэгтгэхэд хялбар байдаг, Хэрэв бид туйлын координатын системд шилжвэл (r, φ ) . Сэлгээний дарааБид хаанаас авдаг:

.(4.18)

Тиймээс фазын хавтгай дээру, vБид логарифмын спираль гэр бүлтэй харьцаж байгаа бөгөөд тэдгээр нь тус бүрдээ байдаггарал үүсэл дэх асимптотик цэг.Ганц цэг нь спираль хэлбэртэй бүх интеграл муруйнуудын асимптот цэг юм, үүрлэсэн найзнайзаа, дуудсан анхаарлаа төвлөрүүл ( зураг.4.8 ) .

Фазын траекторийн дагуу төлөөлөх цэгийн хөдөлгөөний мөн чанарыг авч үзье. (4.17) тэгшитгэлийн эхний хэсгийг үржүүлэху, хоёр дахь нь vнэмээд бид дараахыг авна.

Хаана

Болъё а 1 < 0 (а 1 = Reλ ) . Дараа нь төлөөлөх цэг нь хязгаарлагдмал хугацаанд хүрэхгүйгээр эхлэл рүү тасралтгүй ойртдог. Энэ нь фазын траекторууд нь мушгирах спираль бөгөөд суларсан хэлбэлзэлтэй тохирч байна гэсэн үг юм.хувьсагч. Энэ нь - тогтвортой төвлөрөл .

Тогтвортой зангилааны хувьд тогтвортой фокусын хувьд зөвхөн Ляпуновын нөхцөл хангагдахаас гадна илүү хатуу шаардлага тавьдаг. Тухайлбал, аливаа анхны хазайлтын хувьд систем эцэстээ тэнцвэрийн байрлал руу хүссэн хэмжээндээ ойртох болно. Анхны хазайлт нь зөвхөн өсөхгүй, харин тэг рүү чиглэн ялзардаг ийм тогтвортой байдлыг нэрлэдэг. үнэмлэхүй тогтвортой байдал .

Хэрэв томъёонд байгаа бол (4.18) а 1 >0 , дараа нь төлөөлөх цэг нь гарал үүслээс холдож, бид харьцаж байна тогтворгүй анхаарал . Онгоцноос хөдөлж байх үеду, vфазын хавтгайдx, yспираль нь мөн спираль хэвээр байх боловч гажигтай байх болно.

Хэзээ болохыг одоо авч үзьеа 1 =0 . Онгоц дээрх фазын траекторууду, vтойрог байх болно аль нь онгоцондx,yтохиромжтой эллипс:

Тиймээс, цагтa 1=0 тусгай цэгээр дамжууланx= 0,y= 0 интеграл муруй өнгөрөхгүй. Интеграл муруйнууд нь хаалттай муруйнууд, тухайлбал, бие биендээ шингэсэн эллипсүүд байрладаг ийм тусгаарлагдсан ганц цэгийг төв гэж нэрлэдэг.

Тиймээс (4.7) шинж чанарын тэгшитгэлийн язгуурын шинж чанараас хамааран зургаан төрлийн тэнцвэрт байдал боломжтой. Хавтгай дээрх фазын траекторийн харагдах байдал x, yЭдгээр зургаан тохиолдлыг Зураг дээр үзүүлэв. 4.9.

Цагаан будаа. 4.9.Шугаман тэгшитгэлийн системийн суурин төлөвийн ойролцоох фазын хөрөг зургийн төрлүүд (4.4).

Таван төрлийн тэнцвэрийн төлөв нь бүдүүлэг бөгөөд тэгшитгэлийн баруун талд хангалттай бага өөрчлөлт хийснээр тэдгээрийн шинж чанар өөрчлөгддөггүй (4.4). Энэ тохиолдолд өөрчлөлтүүд нь зөвхөн баруун гар талд төдийгүй тэдгээрийн эхний эрэмбийн деривативуудад бага байх ёстой. Тэнцвэрийн зургаа дахь төлөв - төв нь бүдүүлэг биш юм. Тэгшитгэлийн баруун талын параметрүүдэд бага зэрэг өөрчлөлт хийснээр энэ нь тогтвортой эсвэл тогтворгүй фокус руу ордог.

Бифуркацийн диаграм

Тэмдэглэгээг танилцуулъя:

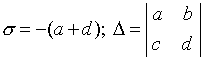. (4.11)

Дараа нь шинж чанарын тэгшитгэлийг дараах хэлбэрээр бичиж болно.

. (4.12)

Тэгш өнцөгт декартын координат бүхий хавтгайг авч үзье с , Д шинж чанарын тэгшитгэлийн язгуур шинж чанараар тодорхойлогддог нэг буюу өөр төрлийн тэнцвэрийн төлөвт тохирох хэсгүүдийг тэмдэглэнэ.

.(4.13)

Тэнцвэрийн төлөвийн тогтвортой байдлын нөхцөл нь y-ийн сөрөг бодит хэсэг байх болнол 1 ба л 2 . Үүний зайлшгүй бөгөөд хангалттай нөхцөл бол тэгш бус байдлыг хангах явдал юмс > 0, Д > 0 . Диаграммд (4.15) энэ нөхцөл нь параметрийн хавтгайн эхний улиралд байрлах цэгүүдтэй тохирч байна. Хэрэв онцгой цэг нь анхаарлын төвд байх болнол 1 ба л 2 цогцолбор. Энэ нөхцөл нь тухайн онгоцны цэгүүдтэй тохирч байна , тэдгээр. параболын хоёр салааны хоорондох цэгүүдс 2 = 4 Д. Хагас тэнхлэгийн цэгүүд с = 0, Д>0, төвийн төрлийн тэнцвэрийн төлөвт тохирно. Үүний нэгэн адил,л 1 ба л 2 - хүчинтэй, гэхдээ өөр өөр шинж тэмдэг, өөрөөр хэлбэл. нэг цэг бол эмээл байх болно Д<0, гэх мэт. Үүний үр дүнд бид параметрийн хавтгайн хуваалтын диаграммыг авдаг с, Д, янз бүрийн төрлийн тэнцвэрийн төлөвт тохирох бүс нутгуудаар.

Цагаан будаа. 4.10.Бифуркацийн диаграм

шугаман тэгшитгэлийн системийн хувьд 4.4

Хэрэв шугаман системийн коэффициентүүд a B C Dзарим параметрээс хамаарах бөгөөд энэ параметр өөрчлөгдөхөд утгууд нь бас өөрчлөгдөх болнос , Д . Хил хязгаарыг давах үед фазын хөрөг зургийн шинж чанар нь чанарын хувьд өөрчлөгддөг. Тиймээс, ийм хил хязгаарыг салаалсан хил гэж нэрлэдэг - хилийн эсрэг талд, систем нь топологийн хувьд өөр өөр фазын хоёр хөрөг, үүний дагуу хоёр өөр төрлийн зан үйлтэй байдаг.

Диаграм нь ийм өөрчлөлтүүд хэрхэн явагдаж болохыг харуулж байна. Хэрэв бид онцгой тохиолдлуудыг - координатын гарал үүслийг хасвал эмээл нь у тэнхлэгийг гатлахад тогтвортой эсвэл тогтворгүй зангилаа руу орж болохыг хялбархан харж болно. Тогтвортой зангилаа нь эмээл эсвэл тогтвортой фокус руу шилжиж болно. Тогтвортой зангилаа-тогтвортой фокус ба тогтворгүй зангилаа-тогтворгүй фокусын шилжилт нь хоёр талт биш гэдгийг анхаарна уу, учир нь энэ тохиолдолд фазын орон зайн топологи өөрчлөгддөггүй. Бид 6-р лекц дээр фазын орон зайн топологи ба салаалсан шилжилтийн талаар илүү дэлгэрэнгүй ярих болно.

Бифуркацийн шилжилтийн үед ганц цэгийн тогтвортой байдлын шинж чанар өөрчлөгддөг. Жишээлбэл, төвөөр дамжуулан тогтвортой фокус нь тогтворгүй фокус болж хувирдаг. Үүнийг салаалсан гэж нэрлэдэг Андронов-Хопфын хуваагдалсудалсан эрдэмтдийн нэрээр. Шугаман бус системд энэ салаалалтаар хязгаарын мөчлөг үүсч, систем өөрөө хэлбэлздэг (лекц 8-ыг үзнэ үү).

Жишээ. Шугаман химийн урвалын систем

Бодис Xгаднаас тогтмол хурдтай урсаж, Y бодис болж хувирч, тухайн бодисын концентрацитай пропорциональ хурдтай. Ю, урвалын хүрээнээс гаргаж авдаг. Тэг дараалалтай гаднаас орж ирж буй бодисыг эс тооцвол бүх урвал нь нэгдүгээр зэрэглэлийнх. Урвалын схем дараах байдалтай байна.

(4.14)

тэгшитгэлийн системээр тодорхойлогддог.

(4.15)

Бид баруун гар талыг тэгтэй тэнцүүлэх замаар суурин концентрацийг олж авна.

.(4.16)

Системийн үе шатны зургийг авч үзье. Системийн хоёр дахь тэгшитгэлийг (4.16) эхний тэгшитгэлд хуваая. Бид авах:

.(4.17)

Тэгшитгэл (4.17) нь фазын хавтгай дээрх хувьсагчдын зан төлөвийг тодорхойлдог. Энэ системийн үе шатны зургийг бүтээцгээе. Эхлээд бид үндсэн изоклинуудыг фазын хавтгай дээр зурдаг. Босоо шүргэгчийн изоклинийн тэгшитгэл:

Хэвтээ шүргэгчийн изоклинийн тэгшитгэл:

Ганц цэг (хөдөлгөөнгүй байдал) нь үндсэн изоклинуудын огтлолцол дээр байрладаг.

Одоо координатын тэнхлэгүүд интеграл муруйг ямар өнцгөөр огтолж байгааг тодорхойлъё.

Хэрвээ x= 0, дараа нь.

Ийнхүү интеграл муруйнууд руу шүргэгч налуугийн тангенс y=y(x),у тэнхлэгийг гатлах x=0, дээд хагас хавтгайд сөрөг байна (хувьсагчуудыг санаарай x, yконцентрацитай байдаг тул бид зөвхөн фазын хавтгайн баруун дээд квадратыг сонирхож байна). Энэ тохиолдолд шүргэгчийн налуу өнцгийн тангенсийн утга нь гарал үүсэлээс холдох тусам нэмэгддэг.

Тэнхлэгийг анхаарч үзээрэй у= 0. Энэ тэнхлэгийн огтлолцол дээр интеграл муруйг тэгшитгэлээр тодорхойлно

At абсцисса тэнхлэгийг гаталж буй интеграл муруйнуудын налуугийн тангенс эерэг бөгөөд нэмэгдэх тусам тэгээс хязгаар хүртэл нэмэгддэг. x.

-д.

Дараа нь цаашид нэмэгдэхийн хэрээр налуугийн тангенс үнэмлэхүй утгаараа буурч, сөрөг хэвээр үлдэж, -1 болно. x ® ¥ . Үндсэн изоклин ба координатын тэнхлэг дээрх интеграл муруй руу шүргэгчийн чиглэлийг мэдэх нь фазын траекторийн зургийг бүхэлд нь бүтээхэд хялбар байдаг.

Ганц цэгийн тогтвортой байдлын шинж чанарыг Ляпуновын аргыг ашиглан тогтооно. Системийн тодорхойлогч шинж чанар нь дараах хэлбэртэй байна.

.

Тодорхойлогчийг өргөжүүлснээр бид системийн шинж чанарын тэгшитгэлийг олж авна. , өөрөөр хэлбэл шинж чанарын тэгшитгэлийн үндэс хоёулаа сөрөг байна. Тиймээс системийн хөдөлгөөнгүй байдал нь тогтвортой зангилаа юм. Үүний зэрэгцээ бодисын концентраци Xхөдөлгөөнгүй төлөв рүү үргэлж нэг хэвийн байх хандлагатай байдаг, Y бодисын концентраци нь мин эсвэл максыг дамжин өнгөрч болно. Ийм систем дэх хэлбэлзлийн горим нь боломжгүй юм.

Тейлорын цуврал нь zol тойргийн аналитик функцүүдийг судлах үр дүнтэй хэрэгсэл болдог. Цагираган мужид аналитик функцүүдийг судлахын тулд эерэг ба сөрөг (z - zq) хүчийг өргөтгөх боломжтой болох нь харагдаж байна. Тейлорын өргөтгөлүүдийг ерөнхийд нь харуулсан хэлбэр. Хоёр цувралын нийлбэр гэж ойлгогдох цувралыг (1) Лорентын цуврал гэж нэрлэдэг. Цуврал (1)-ийн нэгдэх муж нь (2) цуваа бүрийн нийлэх мужуудын нийтлэг хэсэг болох нь тодорхой байна. Түүнийг олъё. Эхний цувралын нэгдэх талбай нь радиус нь Коши-Хадамард томъёогоор тодорхойлогддог тойрог юм. мөн жигд. Хоёрдахь цуваа нь хувьсагчийн хувьд зэрэглэлийн цуваа.(5) цуваа нь нийлэх тойрогтоо m-*oo цогц хувьсагчийн аналитик функцэд нийлэх ба радиусаас бага аль ч тойрогт үнэмлэхүй, жигд нийлдэг. Энэ нь цувралын нийлэх муж (4) нь тойргийн харагдах байдал гэсэн үг юм - Хэрэв дараа нь цуваа (3) ба (4) -ийн нийлэх нийтлэг муж байгаа бол - цуврал (1) байх дугуй цагираг. аналитик функцэд нийлдэг. Түүнээс гадна, ямар ч цагирагт энэ нь туйлын, жигд нийлдэг. Жишээ 1. Рад Лоранын цувралын нийлэх мужийг тодорхойл. Тусгаарлагдсан ганц цэгүүд ба тэдгээрийн ангиллыг (z) дугуй цагирагт нэг утгатай, улс төргүй байх нь коэффициентүүд нь нийлсэн цувааны нийлбэрээр энэ цагирагт төлөөлж болно. Cn нь 7p нь m радиустай тойрог байх томьёогоор тодорхойлогддог бөгөөд R цагираг дотор дурын z цэгийг тогтооцгооё. Радиус нь тэгш бус байдлыг хангадаг r цэгт төвтэй тойрог байгуулж, шинэ цагираг авч үзье.Үржүүлэгт холбогдсон мужид зориулсан Коши интеграл теоремын дагуу нийлбэр (8) дахь интеграл бүрийг тус тусад нь хувиргацгаая. 7d* тойргийн бүх ξ цэгийн хувьд жигд нийлсэн цуваа 1 1-ийн нийлбэр de хамаарал хангагдана.ir> тойргийн бүх ξ цэгийн хувьд хамаарал хангагдана Иймд ^ бутархайг нийлбэрээр илэрхийлж болно. Томъёо (10) ба (12) дахь жигд нийлэх цуваа нь дугуй цагираг дахь аналитик функцууд юм. Тиймээс Кошигийн теоремоор 7/r ба 7r/ тойргийг дурын тойрогоор сольсон тохиолдолд харгалзах интегралын утга өөрчлөгдөхгүй. Энэ нь (10) ба (12) томьёог нэгтгэх боломжийг олгодог.(8)-ын баруун талд байгаа интегралуудыг тэдгээрийн илэрхийлэл (9) ба (11)-ээр тус тус сольсноор бид хүссэн өргөтгөлийг олж авна.З нь дурын томьёо тул цагирагийн цэгээс харахад (14) цуврал нь энэ цагирагны хаа сайгүй f(z) функцэд нийлдэг бөгөөд аль ч цагирагт цуваа нь энэ функцэд туйлын бөгөөд жигд нийлдэг. Одоо (6) хэлбэрийн задрал нь өвөрмөц гэдгийг баталцгаая. Дахиад нэг задрал явагдана гэж бодъё.Тэгвэл R цагираг доторх хаа сайгүй тойрог дээр цуваа (15) жигд нийлдэг. Тэгш байдлын хоёр талыг үржүүлээрэй (үүнд m нь тогтмол бүхэл тоо бөгөөд хоёр цувралын нэр томъёог нэр томъёогоор нэгтгэх. Үүний үр дүнд бид зүүн талдаа, баруун талд нь - Csh. Тиймээс, (4, \u003d St. оноос хойш). m нь дурын тоо, дараа нь коэффициентийг (7) томъёогоор тооцоолсон сүүлчийн тэгшитгэлийн цувралыг (6) 7 цагираг дахь f(z) функцийн Лорантын цуврал гэж нэрлэдэг) Лорантын цувралын коэффициентүүдийн хувьд практикт ховор хэрэглэгддэг, учир нь дүрэм журмын дагуу тэдгээр нь нүсэр тооцоолол шаарддаг.Ихэвчлэн боломжтой бол энгийн функцүүдийн бэлэн Тэйлор өргөтгөлүүдийг ашигладаг.Өргөлтийн өвөрмөц чанар дээр үндэслэн аливаа хууль ёсны арга нь ижил үр дүнд хүргэдэг.Жишээ: 2 Фуисциус /(z) нь хоёр онцгой цэгтэй гэж үзвэл өөр өөр домэйнуудын функцүүдийн Лорентын цуврал өргөтгөлүүдийг авч үзье: Иймээс гурван цагираг домэйн байдаг. ба r = 0 цэг дээр төвлөрсөн. тус бүрд f(r) функц аналитик байна: a) тойрог нь тойргийн гаднах хэсэг юм (Зураг 27). Эдгээр муж бүр дэх /(z) функцийн Лорентын өргөтгөлийг олцгооё. Бид /(z)-ийг энгийн бутархайн нийлбэрээр илэрхийлнэ a) Тойрог хувиргах хамаарлыг (16) дараах байдлаар геометр прогрессийн гишүүний нийлбэрийн томъёог ашиглан бид олж авна. b) |z|-ийн j^j функцийн цуврал (19) тул -z функцийн цагираг энэ цагирагт нийлсэн хэвээр байна. > 1 зөрүүтэй. Тиймээс бид /(z) функцийг дараах байдлаар хувиргана: (19) томъёог дахин ашигласнаар энэ цуврал нь нийлдэг болохыг олж авна. (18) ба (21) тэлэлтүүдийг (20) хамааралд орлуулснаар бид c) -z функцийн тойргийн гадаад байдлыг |z| > 2 диверс ба функцийн цуваа (21) /(z) функцийг дараах хэлбэрээр илэрхийлье: /<*> (18) ба (19) томъёог ашиглан бид OR 1-ийг олж авна. Энэ жишээ нь ижил функцийн хувьд f(z) Лорентын өргөтгөл нь ерөнхийдөө өөр өөр цагиргуудын хувьд өөр хэлбэртэй байгааг харуулж байна. Жишээ 3. Лоранын цуврал функцийн 8 Лоран цувралын задралыг ол. Тусгаарлагдсан ганц цэгүүд ба цагираг хэлбэрийн А муж дахь ангиллыг Бид f (z) функцийн дүрслэлийг дараах хэлбэрээр ашигладаг: мөн хоёр дахь гишүүнийг хувиргана. геометр прогрессийн гишүүний нийлбэрийн томъёог олж авна. Олдсон илэрхийлэлүүдийг томьёо (22)-д орлуулбал бидэнд Жишээ 4 байна. Нимгэн zq = 0-ийн ойролцоох Лорант цувралын функцийг өргөжүүлэх. Аливаа цогцолборын хувьд. , we have Let Энэ өргөтгөл нь дурын z цэгт хүчинтэй байна Ф 0. Энэ тохиолдолд цагираг муж нь нэг z цэгийг хаясан бүхэл бүтэн цогц хавтгай - 0. Энэ мужийг дараах хамаарлаар тодорхойлж болно: Энэ функц нь аналитик юм. бүс нутагт Лоранын цувралын коэффициентүүдийн (13) томъёоноос өмнөх догол мөрөнд дурдсантай ижил үндэслэлээр Kouiw тэгш бус байдлыг олж авч болно. Хэрэв f(z) функц нь тойрог дээр хүрээлэгдсэн бол M нь тогтмол), тусгаарлагдсан ганц цэгүүд Хэрэв цэгийн цагираг хэлбэрийн хөрш байгаа бол zo цэгийг f(z) функцийн тусгаарлагдсан ганц цэг гэнэ. Энэ олонлогийг заримдаа 2o цэгийн цоорсон хөрш гэж нэрлэдэг бөгөөд энд f(z) функц нь нэг утгатай бөгөөд аналитик байдаг. Зо цэгийн хувьд функц нь тодорхойлогдоогүй эсвэл нэг утгатай, аналитик биш юм. Зо цэгт ойртох үед /(z) функцийн үйлдлээс хамааран 3 төрлийн ганц цэгийг ялгадаг. Тусгаарлагдсан ганц цэгийг: 1) хязгаарлагдмал цэг байгаа бол зөөврийн цэг гэж нэрлэдэг Теорем 16. f(z) функцийн тусгаарлагдсан ганц цэг z0 нь зөвхөн zo цэгийн хөрш дэх f(z) функцийн Лорентын өргөтгөл нь үндсэн хэсгийг агуулаагүй тохиолдолд, өөрөөр хэлбэл, зөөврийн ганц цэг болно. Let zo - зөөврийн ганц цэг хэлбэртэй байна. Дараа нь хязгаарлагдмал нэг байдаг ба иймээс f(z) функц нь r цэгийн прокологийн ойролцоо хязгаарлагдмал байна. Бид Коши тэгш бус байдлын тусламжтайгаар тогтооно. p-г дурын жижиг гэж сонгох боломжтой тул бүх коэффициентүүд сөрөг хүч (z - 20) тэгтэй тэнцүү байна: Эсрэгээр, zq цэгийн хөрш дэх /(r) функцийн өргөтгөлийг Лорант зөвхөн зөв хэсгийг агуулна, өөрөөр хэлбэл (23) хэлбэртэй ба, улмаар Тейлор юм. z -* z0-ийн хувьд /(r) функц нь хязгаарын утгатай болохыг хялбархан харж болно: Теорем 17. f(z) функцийн тусгаарлагдсан zq цэгийг зөвхөн J(z) функц байвал салгаж болно. zq цэгийн зарим цоорсон хороололд хязгаарлагдсан, Zgmechai үгүй. r0 нь f(r)-ийн зөөврийн ганц цэг байг. f(r) функц нь th цэгт төвлөрсөн тойрогт аналитик байна гэж үзвэл. Энэ нь цэгийн нэрийг тодорхойлдог - нэг удаагийн. Теорем 18. f(z) функцийн zq тусгаарлагдсан ганц цэг нь тухайн цэгийн ойр орчмын f(z) функцийн Лорентын өргөтгөлийн үндсэн хэсэг нь төгсгөлөг (болон эерэг) тоог агуулж байвал туйл болно. тэгээс өөр гишүүнчлэлийн, өөрөөр хэлбэл, 4 хэлбэртэй байна z0 туйл байг. Түүнээс хойш f(z) функц нь аналитик ба тэгээс өөр байх z0 цэгийн цоорсон хөрш бий болсон. Дараа нь энэ хөршид аналитик функц тодорхойлогддог бөгөөд zq цэг нь функцийн зөөврийн ганц цэг (тэг) буюу h(z) нь аналитик функц бол h(z0) 4 0. нь аналитик юм. zq цэгийн хөрш зэргэлдээ байх ба эндээс бид үүнийг олж авлаа. Одоо f(z) функц нь zo цэгийн цоорсон хэсэгт (24) хэлбэрийн задралтай байна гэж үзье. Энэ нь энэ орчинд f(z) функц нь функцтэй хамт аналитик байна гэсэн үг юм. g(z) функцийн хувьд тэлэлт хүчинтэй бөгөөд үүнээс zq нь g(z) функцийн зөөврийн ганц цэг бөгөөд оршин байх нь тодорхой байна. Дараа нь функц 0-д чиглэдэг - функцийн туйл Өөр нэг энгийн зүйл байна. баримт. G(z) = yw функцийг g(z0) = 0 гэж тохируулснаар zq цэгийн ойролцоох аналитик функцэд өргөтгөж болох тохиолдолд Zq цэг нь f(z) функцийн туйл болно. f(z) функцийн туйлын хэмжээг jfa функцийн тэгийн дараалал гэнэ. 16 ба 18-р теоремууд нь дараах баталгааг илэрхийлж байна. Теорем 19. Энэ цэгийн цоорсон хөрш дэх Лорентын тэлэлтийн гол хэсэг нь хязгааргүй олон тэгээс өөр гишүүнчлэлийн агуулж байгаа тохиолдолд тусгаарлагдсан ганц нимгэн нь үндсэндээ ганц бие болно. Жишээ 5. Функцийн ганц цэг нь zo = 0. Бидэнд Лоран цувралын тусгаарлагдсан ганц цэгүүд ба тэдгээрийн ангилал Тиймээс zo = 0 нь зөөврийн ганц цэг юм. Тэг цэгийн ойролцоох Лорент цувралын /(z) функцийн өргөтгөл нь зөвхөн зөв хэсгийг агуулна: Жишээ 7. f(z) = f(z) функцийн ганц цэг нь zq = 0. Бодит ба төсөөллийн тэнхлэг дээрх энэ функцийн үйлдлийг авч үзье: бодит тэнхлэгт x 0 дээр, төсөөллийн тэнхлэг дээр Иймээс төгсгөлийн аль нь ч үгүй. z -* 0 үед хязгааргүй f(z) хязгаар байхгүй. Иймээс r0 = 0 цэг нь f(z) функцийн үндсэндээ ганц цэг юм. Тэг цэгийн ойролцоо f(z) функцийн Лорентын тэлэлтийг олъё. Аливаа цогцолбор С-ийн хувьд бид тогтоосон. Дараа нь Лорентын өргөтгөл нь z-ийн сөрөг хүчинтэй хязгааргүй тооны гишүүнчлэлийг агуулна.

Болъё zq - f(z) функцын ганц цэг, t.s. f(z)гэхдээ энэ нь аналитик шинж чанартай байдаг (ялангуяа үүнийг тодорхойлоогүй байж болно). Цэгийн ийм цоорсон хороолол байгаа бол zq (өөрөөр хэлбэл, O z - олонлог zq f(z) нь алиатик юм zoдуудсан тусгаарлагдсан ганц цэгфункцууд f(z).Энэ тодорхойлолт нь хэрэгт хадгалагдан үлдсэн zn = oo, хэрэв иод нь нэг цэгийн цоорсон хөрш юм zq = oo багцыг ойлгох z > I - гарал үүсэл дээр төвлөрсөн зарим тойргийн харагдах байдал. Өөрөөр хэлбэл, онцгой цэг Хэрэв энэ цэгийн хөрш зэргэлдээ оршдог бол zq-г тусгаарлагдсан гэж үзнэ. zq. Доорх хаа сайгүй бид зөвхөн нэг утгатай тэмдэгтийн цорын ганц цэгүүдийг (функц f(z)өвөрмөц гэж үздэг).

Функцийн зан төлөвөөс хамаарна f(z)цагт z -> zqГурван төрлийн онцгой цэгүүд байдаг. Тусгаарлагдсан ганц цэг zq функцууд f(z)гэж нэрлэдэг:

1) зөөврийн ганц цэгхэрэв хязгаарлагдмал хязгаар байгаа бол

2) туйлхэрэв хязгаар байгаа бол

3) чухал цэг,хэрэв f(z) нь хязгаарлагдмал, хязгааргүй хязгааргүй z-> zq.

ЖИШЭЭ 26.1. Гурван төрлийн цорын ганц цэг бүгд биелдэг гэдгийг харуулъя. Санаж үз е(z)= цэг zq = 0 нь тусгаарлагдсан байна

Энэ функцийн онцгой цэг. Томъёог (22.12) ашиглан бид өргөтгөлийг олж авна

үүнээс лим байдаг гэсэн үг fi(z)= 1. Тиймээс zq = 0 байна

нь функцийн зөөврийн ганц цэг юм fi(z).

Чиг үүрэг f'j(z) =--- нэг цэг дээр шонтой байна zo= 1 учир нь

2 r"X

Одоо функцийг авч үзье )z(z)= e 1 ^ r ба үүнийг харуул zo = O нь энэ функцийн чухал цэг юм. Хичээж байхдаа zбодит тэнхлэгийн дагуу тэг рүү, функцийн зүүн ба баруун хязгаар f (z)ялгаатай: лим -тай 1 / 1 = 0,лим 1 /* =-тэй os. Энэ нь,

x->0-0 x->0+0

юу f:i(z) 2-ын хувьд төгсгөлтэй ч, төгсгөлгүй ч хязгаар байдаггүй -> Өө, өөрөөр хэлбэл. zq = 0 нь энэ функцийн үндсэн цорын ганц цэг юм. (Зохиол нь чиг хандлагатай байгааг анхаарна уу z-iyтөсөөллийн тэнхлэгийн функц дээр тэг болно

ямар ч хязгаарлалт байхгүй.)

Мэдээжийн хэрэг, тусгаарлагдаагүй онцгой цэгүүд бас байдаг. Жишээлбэл. функц нь цэгүүд дээр туйлтай байдаг z n = -, П= ±1, ±2,...

Үүний үр дүнд, Zq = 0 нь энэ функцийн тусгаарлагдаагүй цорын ганц цэг юм: энэ цэгийн аль ч (дурын жижиг) ойролцоо бусад ганц цэгүүд байдаг. g х.

Болъё зо-функцийн эцсийн тусгаарлагдсан ганц цэг f(z).Дараа нь f(z)цэгийн зарим цоорсон хөрш 0 Zo төстэй байна zoЭнэ хөршийг дотоод радиустай цагираг гэж үзэж болно r = 0. Теорем 25.1-ийн дагуу авч үзэж буй хөршдөө функц f(z)Лорентын цувралд (25.2) өргөжүүлж болно. Бид 2-ын функцийн зан төлөвийг харуулах болно -> zq (өөрөөр хэлбэл ганц цэгийн төрөл zo)задралын үндсэн хэсгийн хэлбэрээс хамаарна (25.2); Энэ нөхцөл байдал нь "үндсэн хэсэг" гэсэн нэр томъёоны гарал үүслийг тайлбарлаж байна.

ТЕОРЕМ 2G.2. f(z) функцийн тусгаарлагдсан цорын ганц zo цэгийг зөвхөн энэ цэгийн цоорсон орчмын Лорап тэлэлт нь оидтой тохиолдолд л салгаж болно.

тэдгээр. зөвхөн зөв хэсгээс бүрдэнэ, үндсэн хэсгийн бүх коэффициентүүд нь сумтай тэнцүү байна.

Баталгаа. 1. Болъё zoнь зөөврийн ганц цэг юм. Лорентын функцийн өргөтгөл гэдгийг баталцгаая f(z)(26.1) хэлбэртэй байна. Ганц цэгээс хойш zoзөөврийн, дараа нь хязгаарлагдмал хязгаар lim байна f(z) = A.Үүний үр дүнд, f(z)зарим цоорсон хороололд хязгаарлагдсан 0 z - цэгийн zq зо,тэдгээр. )(z) бүгдэд зориулсан zэнэ хөршөөс. Ямар ч ав Р. U р /?|, Лоран цувралын коэффициентүүдийн хувьд (25.3) томъёог ашиглана:

Өргөтгөлийн үндсэн хэсгийн коэффициентүүдийн хувьд n =- 1,-2,... Ийм утгын хувьд Пбидэнд байгаа p~n-e 0 цагт Р-> 0. утгаас хойш Рдур мэдэн жижиг сонгож болно, тэгвэл ноён~"дур зоргоороо жижиг байж болно. |c t,|-ээс хойш ^ Ноён~нба cn нь p-ээс хамаарахгүй бол cn = 0 хувьд болон= - 1, -2,..., нотлох ёстой байсан.

2. Одоо Лоран тэлэлт (26.1) хэлбэртэй байна гэж үзье. Цуврал (26.1) нь хүчирхэг цуврал ба. Тиймээс зөвхөн цоорсон хэсэгт төдийгүй бүхэл бүтэн хөршид нийлдэг z-zq түүний дотор цэг zo;түүний хэмжээ S(z)нь аналитик юм z ба S(z) = )(z) 0 z-д - zoР.Тиймээс хязгаарлагдмал хязгаартай лим байдаг )(z)\u003d Pm 5 (r) \u003d 5 (r) - Тиймээс ганц цэг zq

Z->Zo Z-*Zo

нэг удаагийн. Теорем нь батлагдсан.

Сэтгэгдэл. Теоремын нотолгоог харахад зөөврийн ганц цэгийн цоорсон 0 z - zo орчимд функц гарч ирнэ. f(z)нь бүх хөршийн аналитик шинж чанартай S(r) функцтэй давхцдаг z - zo . Тиймээс хэрэв бид /(th) = гэж тохируулбал S(zq), дараа нь функцийн утгыг өөрчлөхгүйгээр f(z)цоорсон хөршийн аль ч цэг дээр бид энэ функцийг r-д аналитик болгодог, i.e. онцлогийг "арилгах". Энэ нь "зөөврийн онцгой байдал" гэсэн нэр томъёог тайлбарладаг. Ийм цэгүүдийг функцийн онцгой цэгүүд биш харин тогтмол гэж үзэх нь зүйн хэрэг юм f(z).

Жишээлбэл, функцийг авч үзье

Жишээ 26.1-д Pm (n) = 1. өөрөөр хэлбэл. онцгой цэг

zq = 0 нь салгаж болно. /i(0) = 1 гэж тохируулснаар бид онцгой байдлыг арилгаж тухайн цэг дээр аналитик функцийг олж авна. zq = 0 (мөн C хавтгайд).

Одоо туйлуудыг Лорентын тэлэлтээр тодорхойлъё.

Теорем 26.3. f(z) функцийн тусгаарлагдсан ганц цэг Zo нь туйл болно, Zq төвтэй Лоран тэлэлтийн үндсэн хэсэг нь зөвхөн хязгаарлагдмал тооны ялгаатай байх үед

n-тэй тэг коэффициентээс:

Баталгаа. 1. Болъё zq - туйл, өөрөөр хэлбэл. лим /( z) = оо.

Лорентын функцийн өргөтгөл гэдгийг баталцгаая f(z)(2G.2) хэлбэртэй байна. Лимээс хойш f(z)= oo. дараа нь цэгийн цоорсон хөрш байдаг

ки zq. тэнд f(z)нь аналитик бөгөөд тэг байхгүй. Дараа нь функц g(z) = 1 /f(z)Мөн энэ цоорсон хороололд аналитик байх болно, мөн лим g(z)= 0. Тиймээс, Зонэг удаагийн *-? *0

функцийн ганц цэг g(z).Дахин тодорхойлъё g(z)цэг дээр zo, оруулах g(zo)= 0. Дараа нь g(z)(цоороогүй) цэгийн бүх хөршид аналитик болдог z 0,болон z0түүний тусгаарлагдсан тэг байх болно. -ээр тэмдэглээрэй Нэнэ тэгийн олон талт (захиалга). §23-т үзүүлсэнчлэн, цэгийн ойролцоо zq функц g(z)хэлбэрээр төлөөлөх боломжтой ((23.2)-ыг үзнэ үү)

болон (z$) f 0 ба y>(z)цэгийн зарим хөршид аналитик юм зо-Учир нь ip(z)цэг дээр тасралтгүй zoболон g>(zo) Ф 0" тэгвэл ip(z)Энэ цэгийн зарим хэсэгт мөн тэг байхгүй. Тиймээс функц 1 /-p(z)Мөн энэ хөршид аналитик байх болно, тиймээс үүнийг Тейлорын цувралд дэлгэн үзүүлэв:

Хаалтуудыг нээж, коэффициентүүдийн тэмдэглэгээг өөрчилснөөр бид сүүлчийн өргөтгөлийг маягт дээр бичнэ.

хаана c_jv = 1>o f 0. Иймд f(r)-ийн Лорентын өргөтгөлийн үндсэн хэсэг нь зөвхөн хязгаарлагдмал тооны гишүүнчлэлийг агуулна; Бид шаардлагатай тэгш байдалд хүрсэн (26.2).

2. Цэгийн цоорсон ойр орчмыг оруулна thфункц )(z)нь Лорентын өргөтгөлөөр (26.2) төлөөлдөг (илүү өргөтгөсөн хэлбэрээр, (26.3)-ыг үзнэ үү), үндсэн хэсэг нь зөвхөн хязгаарлагдмал тооны нэр томъёог агуулдаг ба -г" е 0. Бид үүнийг батлах ёстой Zq - функциональ туйл f(z).Тэгш байдлыг (26.3)-аар үржүүлэх (Г - Г o) iV , бид функцийг авна

(26.4) дэх цуврал нь зөвхөн цоорсон хэсэгт төдийгүй цэгийн бүх орчимд аналитик функцэд нийлдэг хүчирхэг цуваа юм. Zq. Тиймээс функц h(z)Хэрэв бид үүнийг тохиргоогоор th-д сунгавал энэ хөршид аналитик болно h(zo)= s_dg е 0. Дараа нь

Ийнхүү o цэг нь туйл бөгөөд теорем 26.3 батлагдсан болно.

Тэг функцийн олон талт (захиалга). g(z)= 1//(r) гэж нэрлэдэг туйлын захиалгафункц /(r). Хэрвээ N-туйлын дараалал нь th, тэгвэл g(z)= (r - Zo)N ip(z),ба (явах) Ф 0 ба 26.3 теоремын нотлох хэсгийн эхний хэсэгт үзүүлснээр f(r)-ийн тэлэлт (26.3) хэлбэртэй байна, энд c_/v байна. е 0. Эсрэгээр, хэрэв f(r) цуваа (26.3) болон өргөжиж байвал e-z F 0, тэгвэл

т.с. N- f(r) функцийн туйлын дараалал. Энэ замаар, функцийн zq туйлын дараалал/(G) zq цэгийн цоорсон хөрш дэх Лоран тэлэлтийн үндсэн хэсгийн тэргүүлэх тэгээс өөр коэффициентийн тоотой тэнцүү байна.(өөрөөр хэлбэл ийм тоотой тэнцүү). Н,ямар s_dg е 0 ба sp= 0 үед П > N).

Хэрэглээний хувьд тохиромжтой) дараах мэдэгдлийг баталцгаая.

Дүгнэлт 26.4. zq цэг нь уран зохиолын N эрэмбийн туйл юм/(G) хэрвээ мөн л бол/(G) хэлбэрээр төлөөлнө

Энд h(z) нь цэгийн ойролцоох аналитик функц юм th ба h(zo) f 0.

Баталгаа. Чиг үүрэг cp(z) = л/ц(z) r цэгийн зарим хөршид аналитик байна.Үндсэн 26.4-ийн нөхцөл нь дараахтай тэнцүү байна.

Тийм ч учраас zq - олон талт тэг Нфункцууд g(z).улмаар үржвэрийн туйл Нфункцууд /(2).

II жишээ 26.5. Функцийн тусгаарлагдсан ганц цэгүүдийг ол мөн тэдгээрийн төрлийг тодорхойлох.

Д е у к тио н.Тэгсэн цэгүүд (з 2 + 1 )(z+ Z) 2 = 0. Хэрэв z 2 L- 1 = 0 дараа нь 2 = ±gхэрэв (з 4- H) 2 = 0, тэгвэл z= -3. Тиймээс функц нь гурван онцгой цэгтэй байна z= r, 22 = -r, З3 = - 3. Анхаарна уу z:

G -нэгдүгээр эрэмбийн туйл (бид үр дүн 26.4-ийг ашигласан). Үүнтэй адилаар 22 = гэдгийг баталж болно -имөн нэгдүгээр зэргийн шон. Бид 2 цагийн турш:

Үндсэндээ онцгой цэгүүдийг авч үзье.

Теорем 26.6. f(z) функцийн zq тусгаарлагдсан ганц цэг нь zq дээр төвлөрсөн Лорентын өргөтгөлийн үндсэн хэсэг нь zq-ээс хязгааргүй олон ялгаатай байвал үндсэндээ ганц бие болно. тэг, p-тэй коэффициентүүд.

Баталгаа. 26.6 теорем нь 26.2 ба 26.3 теоремуудаас шууд гардаг. Үнэхээр, хэрэв цэг zq нь үндсэндээ ганц бие юм, тэгвэл Лорентын өргөтгөлийн гол хэсэг нь байхгүй эсвэл хязгаарлагдмал тооны нэр томьёо агуулж болохгүй (өөрөөр бол цэг Zq зөөврийн эсвэл шонтой байх болно). Тиймээс үндсэн хэсгийн гишүүний тоо хязгааргүй байх ёстой.

Эсрэгээр, хэрэв үндсэн хэсэг нь хязгааргүй олон гишүүнийг агуулж байвал Zq нь зөөврийн цэг ч биш, туйл ч байж болохгүй. Иймээс энэ цэг нь үндсэндээ онцгой юм.

Тодорхойлолтоос үзэхэд үндсэндээ ганц цэг нь f(2) функц нь хязгаарлагдмал, төгсгөлгүй хязгааргүй байдгаараа тодорхойлогддог. z ->zq. Чухал ач холбогдол бүхий онцгой цэгийн ойролцоо функцийн үйл ажиллагаа хэр жигд бус болох талаар илүү бүрэн гүйцэд ойлголтыг дараах теоремоор өгсөн болно.

Теорем 26.7 (Сочокийн теорем). Хэрэв zq үндсэндээ ганц тоо бол f(z) функцийн цэг), дараа нь дурын комплекс тооЛ, үүнд A =өө, z n -> zo ба байх z n цэгүүдийн дараалал байдаглим f(zn) = ГЭХДЭЭ.

n->os

Баталгаа. Эхлээд хэргийг авч үзье A = oo. 2G.2 теоремын нотолгооны эхний хэсэгт бид хэрэв f(z) r0 цэгийн зарим нэг цоорсон хөршөөр хязгаарлагдсан бол бүх коэффициент c, n = -Үндсэн хэсгийн 1, - 2,... нь 0-тэй тэнцүү байна (ингэснээр th дахь онцгой байдал нь арилдаг). Таамаглалаар r0 нь үндсэндээ ганц цэг тул f(r) функц нь r0 цэгийн цоорсон аль ч хэсэгт хязгааргүй байна. Ийм нарийн 0 Z хорооллыг авч үзье f(zi) > 1 (хэрэв |/(r)| z - zo R/2 цэг байгаа бол z-2 , хаана |/(dd)| > 2 гэх мэт: цоорсон хороололд О 71. rn -e go, lim /(r«) = оо гэдэг нь ойлгомжтой. Иймд A = oo тохиолдолд теорем 26.7

батлагдсан.

Одоо зөвшөөр А f oo. Эхлээд цоорсон хороолол 0 байна гэж үзье

= -ж---- Энэ цоорсон хөршид аналитик байх болно, улмаар

/(G) - ГЭХДЭЭ

улмаар r нь Φ(r) функцийн тусгаарлагдсан ганц цэг юм. Харуулъя. r0 нь Φ(r)-ийн үндсэндээ ганц цэг юм. Буруу байг. Дараа нь хязгаарлагдмал эсвэл хязгааргүй lim Φ(r) байна. Учир нь

/(r) = A +, тэгвэл Hsh /(r) мөн байгаа нь нөхцөлтэй зөрчилдөж байна

F(g) ~ :-*z 0

теоремын үзэл бодол. Тиймээс r0 нь Φ(r) функцийн үндсэндээ ганц цэг юм. Дээр батлагдсан зүйлээс үзэхэд r n o ба lim Φ(r n) = oo байх r n цэгүүдийн дараалал бий. Эндээс

Бид f(r) гэсэн таамаглалын дагуу шаардлагатай мэдэгдлийг нотолсон. Ф А r цэгийн зарим цоорсон хороололд.Одоо үүнийг үнэн биш гэж үзье, i.e. цэгийн дур мэдэн жижиг цоорсон хөршид ийм цэг байдаг G",гэж f(r") = A. Дараа нь дурын Пцоорсон хороололд 0 f(z u) = L. Тиймээс шаардлагатай баталгаа үнэн болно П-юо

бүх тохиолдолд, мөн теорем 26.7 батлагдсан байна.

(Сохоцкийн) теорем 26.7-д зааснаар үндсэндээ ганц цэгийн аль ч (дураар жижиг) цоорсон хөршид f(r) функц нь өргөтгөсөн цогцолбор С хавтгайд дурын тооны ойролцоо утгыг авдаг.

Тусгаарлагдсан онцгой цэгүүдийг судлахын тулд үндсэн функцүүдийн алдартай Тейлорын өргөтгөлүүд ихэвчлэн хэрэгтэй байдаг.

ЖИШЭЭ 2G.8. Функцийн хувьд zq = 0 цорын ганц цэгийн төрлийг тодорхойл

Шийдвэрлэсэн ба e. Бид Тейлорын цувралын тоо болон хуваагчийг r-ийн зэрэглэлээр өргөжүүлэв. (22.11) 3-т орлуулах z r ба 1-ийг хасахын оронд бид авна

(22.12) ашиглан бид хуваагчийн өргөтгөлийг олж авна.

Эдгээр өргөтгөлүүдийн цувралууд нь бүхэл бүтэн € нийлдэг. Бидэнд байгаа

ба /2(2) нь тухайн цэгийн ойролцоо ижил төстэй байна zo = 0 (мөн бүх хавтгайд ч) ба /2(20) Ф 0, тэгвэл h(z)мөн gF 0 цэгийн зарим хөршид аналитик байна.Үндсэн 26.4-т зааснаар цэг Zo = 0 нь захиалгын туйл юм N = 4.

II жишээ 26.9. Функцийн ганц цэгүүдийг ол f(z)= sin j - ба тэдгээрийн төрлийг тодорхойлно.

P e in e and e. Функц нь эцсийн ганц цэгтэй zq = 1. С-ээс бусад цэгүүдэд функц w =--- аналитик; иймээс нүгэл үйлддэг wаналитик байх болно.

Синусын өргөтгөлийг орлуулах (22.12) - r-ийн оронд бид авна.

Бид нүглийн функцийн өргөтгөлийг 20 = 1 цэгийн цоорсон хөршийн Лорант цувралд олж авлаа. Үүссэн өргөтгөл нь сөрөг хүчинтэй (r - 1) хязгааргүй олон гишүүнчлэлийн агуулгыг агуулна. zq = 1 нь чухал онцгой цэг юм (энэ тохиолдолд Лорентын өргөтгөл нь зөвхөн үндсэн хэсгээс бүрдэх ба зөв хэсэг байхгүй).

Энэ тохиолдолд цуврал өргөтгөл хийхгүйгээр өвөрмөц байдлын мөн чанарыг тодорхойлолтоос шууд тогтоох боломжтой байсныг анхаарна уу. Үнэн хэрэгтээ (r") ба (2") нийлдэг дараалал байдаг zo= 1 гэх мэт f(z" n)= 1, /(2") = 0 (ийм дарааллыг өөрөө зааж өгнө үү). Тэгэхээр, f(z)хэзээ хязгааргүй z -> 1 ба эндээс цэг zq - 1 нь үндсэндээ ганц бие юм.

Цэгтэй ойр орших функцийн Лорентын өргөтгөлийн тухай ойлголтыг танилцуулъя Zq = 00 ба энэ цэг дэх онцгой байдлын тэлэлт ба шинж чанарын хоорондын холбоог авч үзье. Тусгаарлагдсан ганц цэг болон түүний төрөл (зөөврийн, туйл, эсвэл үндсэндээ ганц) тодорхойлолтыг тухайн тохиолдолд шилжүүлж байгааг анхаарна уу. zq = oc өөрчлөгдөөгүй. Харин теорем 26.2. Лорентын өргөтгөлийн шинж чанартай холбоотой 26.3 ба 26.6-г өөрчлөх шаардлагатай. Гол нь гишүүд c n (z - 2o) х. П= -1,-2,..., үндсэн хэсэг, төгсгөлийн цэгийн ойролцоо функцийн "‘зөрчил"-ийг тодорхойлох Zq, 2 нь оо руу чиглэдэг тул тэд "зөв" ажиллах болно (0-тэй тэнцүү). Харин ч байнгын хэсгийн гишүүд хамт П= 1,2,... oo хандлагатай болно; тэдгээр нь өвөрмөц байдлын мөн чанарыг тодорхойлдог Zq = oo. Тиймээс oo хөршийн өргөтгөлийн гол хэсэг нь эерэг эрх мэдэл бүхий нэр томъёо байх болно П,ба зөв - сөрөг.

Шинэ хувьсагчийг танилцуулъя w = 12. Чиг үүрэг ТВ= 1/2, u(oo) = 0 байхаар өргөтгөсөн, нэгийг харьцаж, хөрш зэргэлдээ газрын зураглалыг тохирно z > Роноо zq = 00 нь |w|-ийн ойролцоо байна wq = 0. Хэрэв функц f(z)цоорсон хөрш дэх аналитик Р z Zq = oc, дараа нь функц G(w) = f(l/w) 0 wo = 0-ийн шар хөршид аналитик байх болно. 2-ийн хувьд -> oo байх тул w-> 0, тэгвэл

Тийм ч учраас G(w)цэг дээр байна wq = 0 нь ижил төрлийн онцгой байдал юм f(z)цэг дээр Zq = 00. W(w) функцийг wo = 0 цэгийн цоорсон хороололд Лорентын цувралд өргөтгөж үзье.

(26.5)-ын баруун талд байгаа нийлбэрүүд нь өргөтгөлийн зөв ба үндсэн хэсгүүдийг тус тус илэрхийлнэ. Хувьсагч руу шилжье z,орлуулах w = 1/z:

илэрхийлж байна П\u003d -A *, 6 * \u003d 6_ " \u003d хамт pмөн үүнийг анзаарсан G(л/ц) = f(z), бид авдаг

задрал (2G.G) гэж нэрлэдэг zq цэгийн цоорсон хөрш дэх f(z) функцийн Лорент өргөтгөл= oo. (2G.6) дахь эхний нийлбэрийг дуудна баруун хэсэг, хоёр дахь нийлбэр нь гол хэсэгэнэ задрал. Эдгээр нийлбэрүүд нь өргөтгөлийн (26.5) зөв ба үндсэн хэсгүүдтэй тохирч байгаа тул өргөтгөл (26.6) нь 26.2, 26.3, 26.6 теоремуудын аналогийг хангана. Тиймээс дараах теорем нь теорем 26.2-ын аналог юм.

Теорем 26.10. Тусгаарлагдсан ганц цэгZq - os (функц/(G) Зөвхөн энэ цэгийн цоорсон хэсэгт байрлах Лорентын өргөтгөл нь хэлбэртэй байвал салгаж болно.

т.с. зөвхөн зөв хэсгээс бүрдэнэ.

Бид /(oo) = тавьдаг хамтран.Ойролцолд нийлэх цуваа (26.7)-аар тодорхойлогдсон функц z > Рцэгүүд 2o \u003d oc, гэж нэрлэдэг z цэг дээрх аналитик o = oo. (Энэ тодорхойлолт нь функцийн аналитик шинжтэй тэнцэж байгааг анхаарна уу G(w) цэг дээр wo = 0.)

Жишээ 26.11. Функцийн zq = oo ганц цэгийг судал

Хязгаар нь хязгаартай тул zo = oo нь f(r) функцийн зөөврийн ганц цэг юм. Хэрэв бид /(oo) = lim-ийг тавьбал J(z)= 0, тэгвэл f(z)болох болно

цэг дээр tic Зо= os. Харгалзах өргөтгөлийг хэрхэн олохыг харуулъя (26.7). Хувьсагч руу шилжье w = 1 fz.Орлуулах z= 1 /?e, бид авна

(сүүлийн тэгш байдал нь ww = 0 цэгийн цоорсон хөршид хүчинтэй боловч бид тодорхойлолтыг (7(0) = 0) өргөтгөх болно). Үр дүнд нь функц нь онцгой цэгүүдтэй байна. w =±i, w =-1/3, мөн цэг дээр Wq = 0 нь аналитик юм. Өргөтгөх функц G(w)градусаар w(Жишээ 25.7-д хийсэн шиг) ба үр дүнгийн чадлын цувралд орлуулах w = 1/zфункцийн өргөтгөлийг (26.7) авч болно f(z).

Тохиолдолд зориулсан теорем 26.3 zo= oo дараах хэлбэрээр дахин бичигдэнэ.

Теорем 26.12. Тусгаарлагдсан ганц цэгявах = ок f(z) функц нь зөвхөн Лорентын тэлэлтийн үндсэн хэсэг бол туйл болно (26.6) зөвхөн хязгаарлагдмал тооны тэгээс бусад коэффициенттэй"-тай:

Энд цуваа нь ердийн хэсэг, хаалтанд орсон олон гишүүнт нь тэлэлтийн гол хэсэг юм. oc дахь туйлын үржвэрийг туйлын олон тоогоор тодорхойлно wq = 0 функц G(z).Тулгийн олон тал нь тоотой давхцаж байгааг харахад хялбар байдаг Н(26.8) дотор.

Q p | (i 2 + 1) (z + 3) 2

Даалгавар. Функц гэдгийг харуул f(z) =-- -- орсон

цэг zo = oo туйлын захиалга 3.

Чухал онцгой цэгийн 26.6 теоремыг тухайн тохиолдолд дахин бичсэн болно zo= os бараг үгчлэн, бид энэ талаар дэлгэрэнгүй ярихгүй.

Үндсэн ойлголт, тодорхойлолтууд:

f(z) аналитик функцийн тэг нь f(a)=0 байх “a” цэг юм.

f(z) функцийн “n” эрэмбийн тэг нь fn(a)¹0 бол “a” цэг болно.

Хэрэв энэ цэгт "a"-аас өөр ганц цэг байхгүй хөрш байгаа бол "a" ганц цэгийг f(z) функцийн тусгаарлагдсан ганц цэг гэж нэрлэдэг.

Тусгаарлагдсан ганц цэгүүд нь гурван төрөлтэй: .

1 зөөврийн тусгай цэг;

3 чухал ганц цэг.

Ганц цэгийн төрлийг олсон ганц цэг дээрх өгөгдсөн функцийн зан төлөв, түүнчлэн олсон ганц цэгийн ойролцоох функцэд зориулж олж авсан Лоран цувралын хэлбэрт үндэслэн тодорхойлж болно.

Ганц цэгийн төрлийг доторх функцийн үйлдлээр тодорхойлох.

1. Зөөврийн ганц цэг.

f(z) функцийн тусгаарлагдсан ганц а цэгийг хязгаарлагдмал хязгаар байгаа бол зөөврийн гэж нэрлэдэг.

2. Польшууд.

f(z) функцийн тусгаарлагдсан ганц а цэгийг хэрэв туйл гэнэ .

3. Чухал онцгой цэгүүд.

f(z) функцийн тусгаарлагдсан ганц а цэгийг хязгаарлагдмал болон хязгааргүй аль нь ч байхгүй бол чухал ганц цэг гэнэ.

Функцийн тэг ба туйлуудын хооронд дараах хамаарал явагдана.

a цэг нь f(Z) функцийн n дарааллын туйл байхын тулд энэ цэг нь функцийн хувьд n дарааллын тэг байх шаардлагатай бөгөөд хангалттай.

Хэрэв n=1 бол туйлыг энгийн гэж нэрлэдэг.

Тодорхойлолт:Нэг утгатай тэмдэгтийн тусгаарлагдсан ганц цэгийг дараах байдлаар нэрлэнэ.

а) задралын үндсэн хэсэг байхгүй бол салгаж авах боломжтой;

б) үндсэн хэсэг нь хязгаарлагдмал тооны гишүүдийг агуулсан бол туйл;

в) үндсэн хэсэг нь хязгааргүй тооны нэр томьёог агуулсан бол үндсэндээ ганц цэг.

a) Тиймээс зөөврийн ганц цэгийн ойролцоо тэлэлт нь дараах хэлбэртэй байна.

энэ нь |z-a| тойргийн бүх цэгт функцийг илэрхийлнэ

z=a төвд тэгш байдал нь худал, учир нь z=a дээрх функц нь тасалдалтай, баруун тал нь тасралтгүй байна. Хэрэв төв хэсэгт байрлах функцийн утгыг баруун талын утгатай тэнцүү болгон өөрчилвөл цоорхой арилах болно - иймээс нэр нь - зөөврийн.

б) m эрэмбийн туйлын ойролцоо Лоран цувралын өргөтгөл дараах хэлбэртэй байна.

в) Энгийн шонгийн ойролцоо

Хасгалт ба тэдгээрийг тооцоолох томъёо.

Тусгаарлагдсан ганц цэг z 0 дээрх аналитик функцийн f(z) үлдэгдэл нь интегралын утгатай тэнцүү комплекс тоо юм. , f(z) функцийн аналитикийн мужид (өөрөөр хэлбэл 0 цагирагт) байрлах z 0 цэг дээр төвлөрсөн L тойргийн дагуу эерэг чиглэлд авав.<|z-z0|

Тусгаарлагдсан z 0 цэг дэх f(z) функцийн үлдэгдлийг Res f(z 0) эсвэл Res (f(z); z 0) тэмдгээр тэмдэглэнэ. Энэ замаар,

Resf(z0)= . (22.15.1)

Хэрэв бид (22.15.1) томъёонд n=-1-ийг оруулбал бид дараахийг авна.

C-1=

эсвэл Res f(z 0)= C -1 ,

тэдгээр. f(z) функцийн үлдэгдэл z 0 онцгой цэгтэй харьцах нь Лоранын цуврал дахь f(z) функцийн тэлэлт дэх сөрөг илтгэгчтэй эхний гишүүний коэффициенттэй тэнцүү байна.

Суутгалын тооцоо.

Тогтмол эсвэл зөөврийн ганц цэгүүд. Мэдээжийн хэрэг, хэрэв z=z 0 нь f(z) функцийн тогтмол буюу зөөврийн ганц цэг бол Res f(z 0)=0 (эдгээр тохиолдлуудад Лорентын задралд үндсэн хэсэг байхгүй тул c-1= 0).

Туйл. z 0 цэгийг f(z) функцийн энгийн туйл болгоё. Дараа нь z 0 цэгийн ойролцоо байх f(z) функцийн Лорант цуврал дараах хэлбэртэй байна.

Эндээс

Тиймээс энэ тэгшитгэлийг z --z 0 гэж хязгаарт шилжүүлснээр бид олж авна

Resf(z0)=

Үндсэндээ онцгой цэг. Хэрэв z 0 цэг нь f(z) функцийн чухал цорын ганц цэг бол энэ цэг дэх функцийн үлдэгдлийг тооцоолохын тулд ихэвчлэн Лоранын цуврал дахь функцийг өргөтгөх дэх c-1 коэффициентийг шууд тодорхойлдог.

Үйл явдлын ангилал. Үйл явдлын нийлбэр, үржвэр, тэдгээрийн шинж чанар, график дүрслэл.

Үйл явдлуудыг дараахь байдлаар хуваадаг.

1. Санамсаргүй

2. Найдвартай

3. Боломжгүй

Найдвартай - энэ нь эдгээр нөхцөлд зайлшгүй тохиолддог үйл явдал юм (шөнийн дараа өглөө болдог).

Санамсаргүй гэдэг нь тохиолдож болох эсвэл болохгүй (шалгалтанд тэнцэх) үйл явдал юм.

Боломжгүй зүйл бол өгөгдсөн нөхцөлд тохиолдохгүй үйл явдал юм (хайрцагнаас зөвхөн улаан харандаагаар ногоон харандаа аваарай).